人教版九年级上册21.1 一元二次方程教学演示ppt课件

这是一份人教版九年级上册21.1 一元二次方程教学演示ppt课件，共19页。PPT课件主要包含了什么是方程，观察与思考，x2-8x-200，它们有什么共同特点，①都是整式方程，②只含一个未知数，一元二次方程的概念，解由题意得，≠±1，＝－1等内容，欢迎下载使用。

1. 理解一元二次方程的概念并能根据题意列方程．(重点)2. 根据一元二次方程的一般形式，判断其二次项系数、一次项系数和常数项．3. 灵活运用一元二次方程解决简单的实际问题.(难点)
2、什么是一元一次方程？
含有未知数的等式叫方程.
只含有一个未知数，并 且未知数的最高次数是1的整式方程叫一元一次方程.
问题1: 幼儿园某教室矩形地面的长为8m，宽为5m，现准备在地面正中间铺设一块面积为18m2的地毯，四周未铺地毯的条形区域的宽度都相同，你能求出这个宽度吗？
设所求的宽度为x m，那么地毯的长为 m， 宽为 m，根据题意，得方程： .
问题2: 你能否找到其他的五个连续整数，使前三个数的平方和等于后两个数的平方和吗？
设五个连续整数中第一个为x ，那么后四个数为 、 、 、 ，根据题意，得方程： .
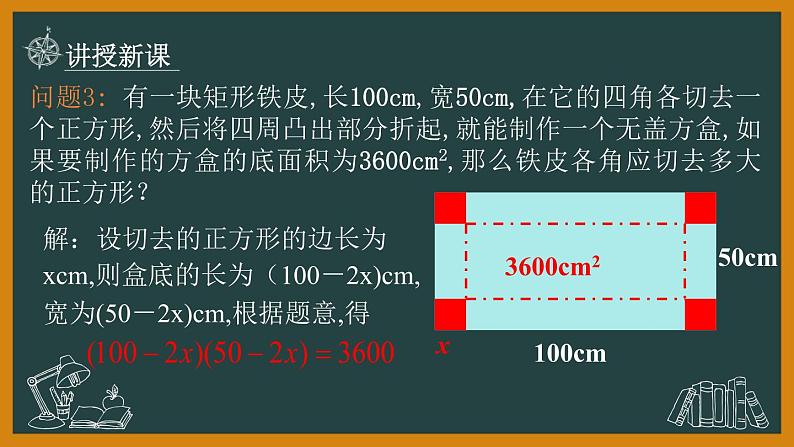
问题3: 有一块矩形铁皮,长100cm,宽50cm,在它的四角各切去一个正方形,然后将四周凸出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600cm2,那么铁皮各角应切去多大的正方形？
解：设切去的正方形的边长为xcm,则盒底的长为（100－2x)cm,宽为(50－2x)cm,根据题意,得
将以上三个方程进行变形：
2x2-13x+11=0
x2-75x+350=0
③未知数的最高次数是2.
只含有一个未知数x的整式方程，并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式，这样的方程叫做一元二次方程.
为什么要限制a≠0，b，c可以为零吗？
一元二次方程的一般形式
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数. bx 称为一次项,b 称为一次项系数. c 称为常数项.
例1 下列选项中，关于x的一元二次方程的是（ ）
例2 下列方程是一元二次方程的有？
(1)、(4)、(6)
例3 a为何值时，下列方程为一元二次方程？
(1)ax2－x=2x2
(2) (a－1)x |a|+1 －2x－7=0.
解：(1)将方程式转化为一般形式，得(a-2)x2-x=0,所以当a-2≠0，即a≠2时，原方程是一元二次方程； (2)由∣a ∣+1 =2，且a-1 ≠0知，当a=-1时，原方程是一元二次方程.
例4 将方程3x(x-1)=5(x+2)化为一般形式，并分别指出它们的二次项、一次项和常数项及它们的系数.
解：化简得 3x2-8x-10=0.
其中二次项是3x2,系数是3；一次项是-8x,系数是-8；常数项是-10.
判断:当未知数的值x=-1或x=0时，方程x²-2=x的两边是否相等.
当x=0时，左边=0²-2=-2 右边=0 因为：左边≠右边
解：当x=-1时，左边=（-1）²-2=1-2=-1 右边=-1 因为：左边=右边
所以x=-1是方程的解.
所以x=0不是方程的解.
一元二次方程的解：能使一元二次方程两边相等的未知数的值叫一元二次方程的解或根.
例5 已知a是方程 x2+2x－2=0 的一个实数根, 求 2a2+4a+2018的值.
1.关于x的方程(k2－1)x2 ＋ 2 (k－1) x ＋ 2k ＋ 2＝0,当k 　　　时，是一元二次方程．当k 　　　时，是一元一次方程．
2.已知方程5x²+mx-6=0的一个根为4，则ｍ的值为_______．
3.已知关于x的一元二次方程x2+ax+a=0的一个根是3，求a的值.
解：由题意把x=3代入方程x2+ax+a=0，得
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
思考:1.若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗?
解：由题意得a+b+c=0
∴方程ax2+bx+c=0 (a≠0)的一个根是1.
2. 若 a-b +c=0,4a+2b +c=0 ，你能通过观察,求出方程ax2+bx+c=0 (a≠0)的一个根吗?