山东省2022年中考数学（五四制）一轮训练：第六章 第3课时 与圆有关的计算(含答案)

这是一份山东省2022年中考数学（五四制）一轮训练：第六章 第3课时 与圆有关的计算(含答案)，共8页。
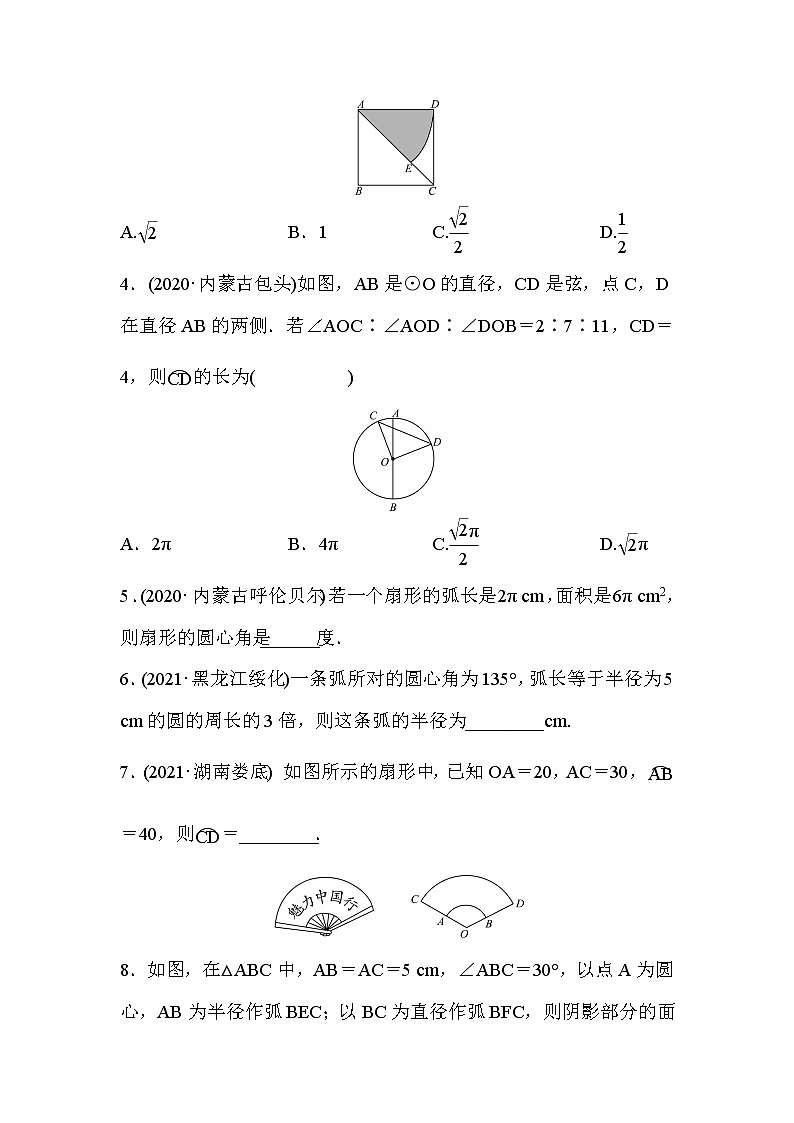
第3课时　与圆有关的计算姓名：______　班级：______　建议用时：40分钟1．(2021·四川成都)如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画圆，则图中阴影部分的面积为(　　)A．4π B．6π C．8π D．12π2．(2021·四川遂宁)如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为F，若⊙O的半径为4，∠CDF＝15°，则阴影部分的面积为(　　)A．16π－12 B．16π－24C．20π－12 D．20π－243．(2020·云南)如图，正方形ABCD的边长为4，以点A为圆心，AD为半径，画圆弧DE得到扇形DAE(阴影部分，点E在对角线AC上)．若扇形DAE正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是(　　　　　)A. B．1 C. D.4．(2020·内蒙古包头)如图，AB是⊙O的直径，CD是弦，点C，D在直径AB的两侧．若∠AOC∶∠AOD∶∠DOB＝2∶7∶11，CD＝4，则的长为(　　　　　)A．2π B．4π C. D.π5．(2020·内蒙古呼伦贝尔)若一个扇形的弧长是2π cm，面积是6π cm2，则扇形的圆心角是______度．6．(2021·黑龙江绥化)一条弧所对的圆心角为135°，弧长等于半径为5 cm的圆的周长的3倍，则这条弧的半径为________ cm.7．(2021·湖南娄底) 如图所示的扇形中，已知OA＝20，AC＝30，＝40，则＝________．8．如图，在△ABC中，AB＝AC＝5 cm，∠ABC＝30°，以点A为圆心，AB为半径作弧BEC；以BC为直径作弧BFC，则阴影部分的面积为________．9．(2021·浙江湖州)如图，已知在矩形ABCD中，AB＝1，BC＝，点P是AD边上的一个动点，连接BP，点C关于直线BP的对称点为C1，当点P运动时，点C1也随之运动．若点P从点A运动到点D，则线段CC1扫过的区域的面积是(　　)A．π   B．π＋ C.   D．2π10．如图，正方形ABCD内的图形来自中国古代的太极图，正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．设正方形ABCD的面积为S，黑色部分面积为S1，则S1∶S的比值为(　　)A.   B. C.   D.11．(2021·四川凉山州)如图，将△ABC绕点C顺时针旋转120°得到△A′B′C.已知AC＝3，BC＝2，则线段AB扫过的图形(阴影部分)的面积为________．12．(2021·湖北襄阳)如图，直线AB经过⊙O上的点C，直线BO与⊙O交于点F和点D，OA与⊙O交于点E，与DC交于点G，OA＝OB，CA＝CB.(1)求证：AB是⊙O的切线；(2)若FC∥OA，CD＝6，求图中阴影部分的面积．     13．(2019·淄博)如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线AD交BC于点D，点E在AC上，以AE为直径的⊙O经过点D.(1)求证：①BC是⊙O的切线；②CD2＝CE·CA；(2)若点F是劣弧AD的中点，且CE＝3，试求阴影部分的面积．   14．(2021·湖南邵阳)某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料，其中AB＝AC，AD⊥BC.将扇形AEF围成圆锥时，AE，AF恰好重合．(1)求这种加工材料的顶角∠BAC的大小；(2)若圆锥底面圆的直径ED为5 cm，求加工材料剩余部分(图中阴影部分)的面积．(结果保留π)     15．(2021·青海)如图，一根5 m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动)，那么小羊A在草地上最大活动区域的面积是(　　)A.π m2   B.π m2C.π m2   D.π m216．(2021·河北)如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为An(n为1～12的整数)，过点A7作⊙O的切线交A1A11延长线于点P.(1)通过计算比较直径和劣弧A7A11长度哪个更长；(2)连接A7A11，则A7A11和PA1有什么特殊位置关系？请简要说明理由；(3)求切线长PA7的值．     参考答案1．D　2.A　3.D　4.D　5.60　6.40　7.1008. cm2　9.B　10.A　11.　12．(1)证明：如图，连接OC.∵OA＝OB, CA＝CB，∴OC⊥AB.∵OC是⊙O的半径，∴AB是⊙O的切线．(2)解：S阴影＝2π－.13．(1)证明：①如图，连接OD.∵AD是∠BAC的平分线，∴∠DAB＝∠DAO.∵OD＝OA，∴∠DAO＝∠ODA，则∠DAB＝∠ODA，∴DO∥AB.∵∠B＝90°，∴∠ODB＝90°，又∵OD是⊙O的半径，∴BC是⊙O的切线．②如图，连接DE.∵BC是⊙O的切线，∴∠CDO＝∠CDE＋∠EDO＝90°.∵AE是⊙O的直径，∴∠ADE＝90°，∴∠DEA＋∠DAE＝90°.∵OE＝OD，∴∠OED＝∠ODE，∴∠CDE＝∠DAC.∵∠C＝∠C，∴△CDE∽△CAD，∴＝，∴CD2＝CE·CA.(2)解：S阴影＝.14．解：(1)∠BAC＝90°.(2)S阴影＝(100－25π)cm2.15．B16．解：(1)由题意得，∠A7OA11＝120°，∴A7A11的长＝＝4π＞12，∴A7A11比直径长．(2)结论：PA1⊥A7A11.理由略．(3)PA7＝12.