广西河池三年（2020-2022）中考数学真题分类汇编-03解答题

这是一份广西河池三年（2020-2022）中考数学真题分类汇编-03解答题，共36页。试卷主要包含了2+|﹣|，，其中x＝2021，，其中a＝3，先化简，再计算，2﹣4×，某水果市场销售一种香蕉等内容，欢迎下载使用。
广西河池三年（2020-2022）中考数学真题分类汇编-03解答题
一．实数的运算（共1小题）
1．（2021•河池）计算：+4﹣1﹣（）2+|﹣|．
二．整式的混合运算—化简求值（共1小题）
2．（2021•河池）先化简，再求值：（x+1）2﹣x（x+1），其中x＝2021．
三．分式的化简求值（共2小题）
3．（2022•河池）先化简，再求值：÷﹣（2a﹣1），其中a＝3．
4．（2020•河池）先化简，再计算：+，其中a＝2．
四．二次根式的混合运算（共2小题）
5．（2022•河池）计算：|﹣2|﹣3﹣1﹣×+（π﹣5）0．
6．（2020•河池）计算：（﹣3）0++（﹣3）2﹣4×．
五．一元一次不等式的应用（共1小题）
7．（2022•河池）为改善村容村貌，阳光村计划购买一批桂花树和芒果树．已知桂花树的单价比芒果树的单价多40元，购买3棵桂花树和2棵芒果树共需370元．
（1）桂花树和芒果树的单价各是多少元？
（2）若该村一次性购买这两种树共60棵，且桂花树不少于35棵．设购买桂花树的棵数为n，总费用为w元，求w关于n的函数关系式，并求出该村按怎样的方案购买时，费用最低？最低费用为多少元？
六．一次函数的应用（共2小题）
8．（2021•河池）为庆祝中国共产党成立100周年，某校组织九年级全体师生前往广西农民运动讲习所旧址列宁岩参加“学党史、感党恩、听党话、跟党走”的主题活动，需要租用甲、乙两种客车共6辆．已知甲、乙两种客车的租金分别为450元/辆和300元/辆，设租用乙种客车x辆，租车费用为y元．
（1）求y与x之间的函数关系式（写出自变量的取值范围）；
（2）若租用乙种客车的数量少于甲种客车的数量，租用乙种客车多少辆时，租车费用最少？最少费用是多少元？
9．（2020•河池）某水果市场销售一种香蕉．甲店的香蕉价格为4元/kg；乙店的香蕉价格为5元/kg，若一次购买6kg以上，超过6kg部分的价格打7折．
（1）设购买香蕉xkg，付款金额y元，分别就两店的付款金额写出y关于x的函数解析式；
（2）到哪家店购买香蕉更省钱？请说明理由．
七．待定系数法求反比例函数解析式（共1小题）
10．（2020•河池）如图，在平面直角坐标系xOy中，A（﹣1，2）．
（1）将点A向右平移3个单位长度，再向上平移1个单位长度，得到点B，则点B的坐标是　 　．
（2）点C与点A关于原点O对称，则点C的坐标是　 　．
（3）反比例函数的图象经过点B，则它的解析式是　 　．
（4）一次函数的图象经过A，C两点，则它的解析式是　 　．

八．二次函数综合题（共3小题）
11．（2022•河池）在平面直角坐标系中，抛物线L1：y＝ax2+2x+b与x轴交于两点A，B（3，0），与y轴交于点C（0，3）．
（1）求抛物线L1的函数解析式，并直接写出顶点D的坐标；
（2）如图，连接BD，若点E在线段BD上运动（不与B，D重合），过点E作EF⊥x轴于点F，设EF＝m，问：当m为何值时，△BFE与△DEC的面积之和最小；
（3）若将抛物线L1绕点B旋转180°得抛物线L2，其中C，D两点的对称点分别记作M，N．问：在抛物线L2的对称轴上是否存在点P，使得以B，M，P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

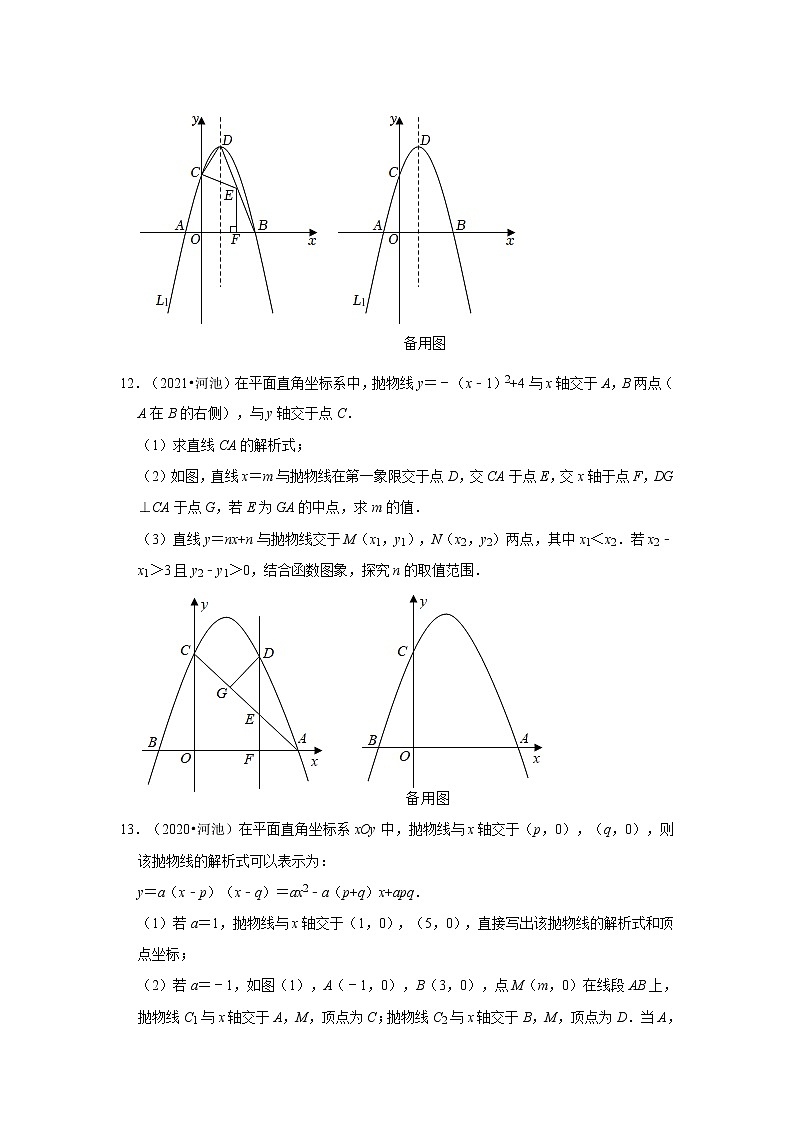
12．（2021•河池）在平面直角坐标系中，抛物线y＝﹣（x﹣1）2+4与x轴交于A，B两点（A在B的右侧），与y轴交于点C．
（1）求直线CA的解析式；
（2）如图，直线x＝m与抛物线在第一象限交于点D，交CA于点E，交x轴于点F，DG⊥CA于点G，若E为GA的中点，求m的值．
（3）直线y＝nx+n与抛物线交于M（x1，y1），N（x2，y2）两点，其中x1＜x2．若x2﹣x1＞3且y2﹣y1＞0，结合函数图象，探究n的取值范围．

13．（2020•河池）在平面直角坐标系xOy中，抛物线与x轴交于（p，0），（q，0），则该抛物线的解析式可以表示为：
y＝a（x﹣p）（x﹣q）＝ax2﹣a（p+q）x+apq．
（1）若a＝1，抛物线与x轴交于（1，0），（5，0），直接写出该抛物线的解析式和顶点坐标；
（2）若a＝﹣1，如图（1），A（﹣1，0），B（3，0），点M（m，0）在线段AB上，抛物线C1与x轴交于A，M，顶点为C；抛物线C2与x轴交于B，M，顶点为D．当A，C，D三点在同一条直线上时，求m的值；
（3）已知抛物线C3与x轴交于A（﹣1，0），B（3，0），线段EF的端点E（0，3），F（4，3）．若抛物线C3与线段EF有公共点，结合图象，在图（2）中探究a的取值范围．

九．全等三角形的判定与性质（共2小题）
14．（2021•河池）如图，在Rt△ABC中，∠A＝90°，AB＝4，AC＝3，D，E分别是AB，BC边上的动点，以BD为直径的⊙O交BC于点F．
（1）当AD＝DF时，求证：△CAD≌△CFD；
（2）当△CED是等腰三角形且△DEB是直角三角形时，求AD的长．

15．（2020•河池）（1）如图（1），已知CE与AB交于点E，AC＝BC，∠1＝∠2．求证：△ACE≌△BCE．
（2）如图（2），已知CD的延长线与AB交于点E，AD＝BC，∠3＝∠4．探究AE与BE的数量关系，并说明理由．

一十．平行四边形的判定（共1小题）
16．（2022•河池）如图，点A，F，C，D在同一直线上，AB＝DE，AF＝CD，BC＝EF．
（1）求证：∠ACB＝∠DFE；
（2）连接BF，CE，直接判断四边形BFEC的形状．

一十一．切线的判定与性质（共1小题）
17．（2020•河池）如图，AB是⊙O的直径，AB＝6，OC⊥AB，OC＝5，BC与⊙O交于点D，点E是的中点，EF∥BC，交OC的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）CG∥OD，交AB于点G，求CG的长．

一十二．圆的综合题（共1小题）
18．（2022•河池）如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D．且∠PCA＝∠CBD．
（1）求证：PC为⊙O的切线；
（2）若PC＝2BO，PB＝12，求⊙O的半径及BE的长．

一十三．作图—应用与设计作图（共1小题）
19．（2021•河池）如图，∠CAD是△ABC的外角．
（1）尺规作图：作∠CAD的平分线AE（不写作法，保留作图痕迹，用黑色墨水笔将痕迹加黑）；
（2）若AE∥BC，求证：AB＝AC．

一十四．作图-位似变换（共1小题）
20．（2022•河池）如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．
（1）画出与△ABC关于y轴对称的△A1B1C1；
（2）以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2：1，并写出点B2的坐标．

一十五．解直角三角形的应用-仰角俯角问题（共2小题）
21．（2022•河池）如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度（结果保留整数．参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65）．

22．（2021•河池）如图，小明同学在民族广场A处放风筝，风筝位于B处，风筝线AB长为100m，从A处看风筝的仰角为30°，小明的父母从C处看风筝的仰角为50°．
（1）风筝离地面多少m？
（2）A、C相距多少m？
（结果保留小数点后一位，参考数据：sin30°＝0.5，cos30°≈0.8660，tan30°≈0.5774，sin50°≈0.7760，cos50°≈0.6428，tan50°≈1.1918）

一十六．扇形统计图（共1小题）
23．（2020•河池）某校举行了主题为“防溺水，保安全”的知识竞赛活动．赛后随机抽取了50名参赛学生的成绩进行相关统计，整理得尚未完整的频数分布表和扇形统计图．现累计了40名参赛学生的成绩，余下10名参赛学生的成绩尚未累计，这10名学生成绩如下（单位：分）：75，63，76，87，69，78，82，75，63，71．
频数分布表
组别
分数段
划记
频数
A
60＜x≤70
正　 　
　 　
B
70＜x≤80
正正　 　
　 　
C
80＜x≤90
正正正正　 　
　 　
D
90＜x≤100
正　 　
　 　
（1）在频数分布表中补全各组划记和频数；
（2）求扇形统计图中B组所对应的圆心角的度数；
（3）该校有2000名学生参加此次知识竞赛，估计成绩在80＜x≤100的学生有多少人？

一十七．条形统计图（共1小题）
24．（2021•河池）为了解本校九年级学生的体质健康情况，李老师随机抽取35名学生进行了一次体质健康测试，根据测试成绩制成统计图表．
组别
分数段
人数
A
x＜60
2
B
60≤x＜75
5
C
75≤x＜90
a
D
x≥90
12
请根据上述信息解答下列问题：
（1）本次调查属于 　 　调查，样本容量是 　 　；
（2）表中的a＝　 　，样本数据的中位数位于 　 　组；
（3）补全条形统计图；
（4）该校九年级学生有980人，估计该校九年级学生体质健康测试成绩在D组的有多少人？

一十八．列表法与树状图法（共1小题）
25．（2022•河池）为喜迎中国共产党第二十次全国代表大会的召开，红星中学举行党史知识竞赛．团委随机抽取了部分学生的成绩作为样本，把成绩按达标，良好，优秀，优异四个等级分别进行统计，并将所得数据绘制成如下不完整的统计图．

请根据图中提供的信息，解答下列问题：
（1）本次调查的样本容量是 　 　，圆心角β＝　 　度；
（2）补全条形统计图；
（3）已知红星中学共有1200名学生，估计此次竞赛该校获优异等级的学生人数为多少？
（4）若在这次竞赛中有A，B，C，D四人成绩均为满分，现从中抽取2人代表学校参加县级比赛．请用列表或画树状图的方法求出恰好抽到A，C两人同时参赛的概率．

参考答案与试题解析
一．实数的运算（共1小题）
1．（2021•河池）计算：+4﹣1﹣（）2+|﹣|．
【解答】解：原式＝2+﹣+
＝3．
二．整式的混合运算—化简求值（共1小题）
2．（2021•河池）先化简，再求值：（x+1）2﹣x（x+1），其中x＝2021．
【解答】解：原式＝x2+2x+1﹣x2﹣x
＝x+1，
当x＝2021时，
原式＝2021+1
＝2022．
另解：原式＝（x+1）（x+1﹣x）
＝x+1，
当x＝2021时，
原式＝2022．
三．分式的化简求值（共2小题）
3．（2022•河池）先化简，再求值：÷﹣（2a﹣1），其中a＝3．
【解答】解：原式＝×﹣（2a﹣1）
＝a﹣2a+1
＝﹣a+1，
当a＝3时，原式＝﹣3+1＝﹣2．
4．（2020•河池）先化简，再计算：+，其中a＝2．
【解答】解：原式＝+
＝+
＝，
当a＝2时，原式＝＝3．
四．二次根式的混合运算（共2小题）
5．（2022•河池）计算：|﹣2|﹣3﹣1﹣×+（π﹣5）0．
【解答】解：原式＝2﹣﹣2+1
＝．
6．（2020•河池）计算：（﹣3）0++（﹣3）2﹣4×．
【解答】解：原式＝1+2+9﹣2
＝10．
五．一元一次不等式的应用（共1小题）
7．（2022•河池）为改善村容村貌，阳光村计划购买一批桂花树和芒果树．已知桂花树的单价比芒果树的单价多40元，购买3棵桂花树和2棵芒果树共需370元．
（1）桂花树和芒果树的单价各是多少元？
（2）若该村一次性购买这两种树共60棵，且桂花树不少于35棵．设购买桂花树的棵数为n，总费用为w元，求w关于n的函数关系式，并求出该村按怎样的方案购买时，费用最低？最低费用为多少元？
【解答】解：（1）设桂花树的单价是x元，则芒果树的单价是（x﹣40）元，
根据题意得：3x+2（x﹣40）＝370，
解得x＝90，
∴x﹣40＝90﹣40＝50，
答：桂花树的单价是90元，芒果树的单价是50元；
（2）根据题意得：w＝90n+50（60﹣n）＝40n+3000，
∴w关于n的函数关系式为w＝40n+3000，
∵40＞0，
∴w随n的增大而增大，
∵桂花树不少于35棵，
∴n≥35，
∴n＝35时，w取最小值，最小值为40×35+3000＝4400（元），
此时60﹣n＝60﹣35＝25（棵），
答：w关于n的函数关系式为w＝40n+3000，购买桂花树35棵，购买芒果树25棵时，费用最低，最低费用为4400元．
六．一次函数的应用（共2小题）
8．（2021•河池）为庆祝中国共产党成立100周年，某校组织九年级全体师生前往广西农民运动讲习所旧址列宁岩参加“学党史、感党恩、听党话、跟党走”的主题活动，需要租用甲、乙两种客车共6辆．已知甲、乙两种客车的租金分别为450元/辆和300元/辆，设租用乙种客车x辆，租车费用为y元．
（1）求y与x之间的函数关系式（写出自变量的取值范围）；
（2）若租用乙种客车的数量少于甲种客车的数量，租用乙种客车多少辆时，租车费用最少？最少费用是多少元？
【解答】解：（1）设租用乙种客车x辆，租车费用为y元，依题意得：
y＝450（6﹣x）+300x，
整理得：y＝﹣150x+2700（0＜x＜6）；
（2）∵租用乙种客车的数量少于甲种客车的数量，
∴x＝1或x＝2，
当x＝1时，y＝﹣150×1+2700＝2550，
当x＝2时，y＝﹣150×2+2700＝2400，
故租用乙种客车2辆时，租车费用最少，为2400元．
另一种思路：
∵租用乙种客车的数量少于甲种客车的数量，
∴x＜6﹣x，
解得x＜3．
由（1）知y＝﹣150x+2700，
∵﹣150＜0，
∴y随x的增大而减小．
∵x为正整数，
∴当x＝2时，y取最小值，此时y＝﹣150×2+2700＝2400．
故租用乙种客车2辆时，租车费用最少，为2400元．
答：租用乙种客车2辆时，租车费用最少，为2400元．
9．（2020•河池）某水果市场销售一种香蕉．甲店的香蕉价格为4元/kg；乙店的香蕉价格为5元/kg，若一次购买6kg以上，超过6kg部分的价格打7折．
（1）设购买香蕉xkg，付款金额y元，分别就两店的付款金额写出y关于x的函数解析式；
（2）到哪家店购买香蕉更省钱？请说明理由．
【解答】解：（1）甲商店：y＝4x
乙商店：y＝．
（2）当x＜6时，
此时甲商店比较省钱，
当x≥6时，
令4x＝30+3.5（x﹣6），
解得：x＝18，
此时甲乙商店的费用一样，
当6≤x＜18时，
此时甲商店比较省钱，
当x＞18时，
此时乙商店比较省钱．
七．待定系数法求反比例函数解析式（共1小题）
10．（2020•河池）如图，在平面直角坐标系xOy中，A（﹣1，2）．
（1）将点A向右平移3个单位长度，再向上平移1个单位长度，得到点B，则点B的坐标是　（2，3）　．
（2）点C与点A关于原点O对称，则点C的坐标是　（1，﹣2）　．
（3）反比例函数的图象经过点B，则它的解析式是　y＝　．
（4）一次函数的图象经过A，C两点，则它的解析式是　y＝﹣2x　．

【解答】解：（1）将点A向右平移3个单位长度，再向上平移1个单位长度，得到点B，则点B的坐标是（2，3）；
（2）点C与点A关于原点O对称，则点C的坐标是（1，﹣2）；
（3）设反比例函数解析式为y＝，
把B（2，3）代入得：k＝6，
∴反比例函数解析式为y＝；
（4）设一次函数解析式为y＝mx+n，
把A（﹣1，2）与C（1，﹣2）代入得：，
解得：，
则一次函数解析式为y＝﹣2x．
故答案为：（1）（2，3）；（2）（1，﹣2）；（3）y＝；（4）y＝﹣2x．
八．二次函数综合题（共3小题）
11．（2022•河池）在平面直角坐标系中，抛物线L1：y＝ax2+2x+b与x轴交于两点A，B（3，0），与y轴交于点C（0，3）．
（1）求抛物线L1的函数解析式，并直接写出顶点D的坐标；
（2）如图，连接BD，若点E在线段BD上运动（不与B，D重合），过点E作EF⊥x轴于点F，设EF＝m，问：当m为何值时，△BFE与△DEC的面积之和最小；
（3）若将抛物线L1绕点B旋转180°得抛物线L2，其中C，D两点的对称点分别记作M，N．问：在抛物线L2的对称轴上是否存在点P，使得以B，M，P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

【解答】解：（1）∵y＝ax2+2x+b经过B（3，0），C（0，3），
∴，
∴，
∴抛物线的解析式为y＝﹣x2+2x+3，
∵y＝﹣（x﹣1）2+4，
∴抛物线的顶点D（1，4）；

（2）如图1中，连接BC，过点C作CH⊥BD于点H．设抛物线的对称轴交x轴于点T．

∵C（0，3），B（3，0），D（1，4），
∴BC＝3，CD＝，BD＝＝2，
∴BC2+CD2＝BD2，
∴∠BCD＝90°，
∵•CD•CB＝•BD•CH，
∴CH＝＝，
∵EF⊥x轴，DT⊥x轴，
∴EF∥DT，
∴＝＝，
∴＝＝，
∴BE＝m，BF＝m，
∴△BFE与△DEC的面积之和S＝×（2﹣m）×+×m×m＝（m﹣）2+，
∵＞0，
∴S有最小值，最小值为，此时m＝，
∴m＝时，△BFE与△DEC的面积之和有最小值．

（3）存在．
理由：如图2中，由题意抛物线L2的对称轴x＝5，M（6，﹣3）．

设P（5，m），
当BP＝BM＝3时，22+m2＝（3）2，
∴m＝±，
∴P1（5，），P2（5，﹣），
当PB＝PM时，22+m2＝12+（m+3）2，
解得，m＝﹣1，
∴P3（5，﹣1），
当BM＝PM时，（3）2＝12+（m+3）2，
解得，m＝﹣3±，
∴P4（5，﹣3+），P5（5，﹣3﹣），
综上所述，满足条件的点P的坐标为P1（5，），P2（5，﹣），P3（5，﹣1），P4（5，﹣3+），P5（5，﹣3﹣）．
12．（2021•河池）在平面直角坐标系中，抛物线y＝﹣（x﹣1）2+4与x轴交于A，B两点（A在B的右侧），与y轴交于点C．
（1）求直线CA的解析式；
（2）如图，直线x＝m与抛物线在第一象限交于点D，交CA于点E，交x轴于点F，DG⊥CA于点G，若E为GA的中点，求m的值．
（3）直线y＝nx+n与抛物线交于M（x1，y1），N（x2，y2）两点，其中x1＜x2．若x2﹣x1＞3且y2﹣y1＞0，结合函数图象，探究n的取值范围．

【解答】解：（1）在y＝﹣（x﹣1）2+4中，令x＝0得y＝3，令y＝0得x＝﹣1或3，
∴A（3，0），B（﹣1，0），C（0，3），
设直线CA的解析式为y＝kx+b，则，
解得，
∴直线CA的解析式为y＝﹣x+3；
（2）∵直线x＝m与抛物线在第一象限交于点D，交CA于点E，交x轴于点F，
∴D（m，﹣（m﹣1）2+4），且0＜m＜3，E（m，﹣m+3），F（m，0），
∴AF＝3﹣m，DE＝﹣（m﹣1）2+4﹣（﹣m+3）＝﹣m2+3m，
∵A（3，0），C（0，3），
∴∠EAF＝45°，△EAF是等腰直角三角形，
∴AE＝AF＝3﹣m，∠DEG＝∠AEF＝45°，
∴△DEG是等腰直角三角形，
∴DE＝GE，
∵E为GA的中点，
∴GE＝AE＝3﹣m，
∴﹣m2+3m＝（3﹣m），
解得m＝2或m＝3，
∵m＝3时，D与A重合，舍去，
∴m＝2；
（3）由得或，
①若3﹣n＞﹣1，即n＜4，如图：

∵x2﹣x1＞3且y2﹣y1＞0，
∴3﹣n﹣（﹣1）＞3，且﹣n2+4n﹣0＞0，
解得0＜n＜1；
②若3﹣n＜﹣1，即n＞4，同理可得：
﹣1﹣（3﹣n）＞3且0﹣（﹣n2+4n）＞0，
解得n＞7，
综上所述，n的取值范围是0＜n＜1或n＞7．
13．（2020•河池）在平面直角坐标系xOy中，抛物线与x轴交于（p，0），（q，0），则该抛物线的解析式可以表示为：
y＝a（x﹣p）（x﹣q）＝ax2﹣a（p+q）x+apq．
（1）若a＝1，抛物线与x轴交于（1，0），（5，0），直接写出该抛物线的解析式和顶点坐标；
（2）若a＝﹣1，如图（1），A（﹣1，0），B（3，0），点M（m，0）在线段AB上，抛物线C1与x轴交于A，M，顶点为C；抛物线C2与x轴交于B，M，顶点为D．当A，C，D三点在同一条直线上时，求m的值；
（3）已知抛物线C3与x轴交于A（﹣1，0），B（3，0），线段EF的端点E（0，3），F（4，3）．若抛物线C3与线段EF有公共点，结合图象，在图（2）中探究a的取值范围．

【解答】解：（1）由题意抛物线的解析式为y＝（x﹣1）（x﹣5）＝x2﹣6x+5＝（x﹣3）2﹣4，
∴y＝x2﹣6x+5，抛物线的顶点坐标为（3，﹣4）．

（2）如图1中，过点C作CE⊥AB于E，过点D作DF⊥AB于F．



由题意抛物线C1为y＝﹣（x+1）（x﹣m）＝﹣（x﹣）2+，
∴C（，），
抛物线C2为y＝﹣（x﹣m）（x﹣3）＝﹣（x﹣）2+，
∴D（，），
∵A，C，D共线，CE∥DF，
∴＝，
∴＝，
解得m＝，
经检验，m＝ 是分式方程的解，
∴m＝．

（3）如图2﹣1，当a＞0时，

设抛物线的解析式为y＝a（x+1）（x﹣3），
当抛物线经过F（4，3）时，3＝a×5×1，
∴a＝，
观察图象可知当a≥时，满足条件．
如图2﹣2中，当a＜0时，顶点在线段EF上时，顶点为（1，3），

把（1，3）代入y＝a（x+1）（x﹣3），可得a＝﹣，
观察图象可知当a≤﹣时，满足条件，
综上所述，满足条件的a的范围为：a≥或a≤﹣．
九．全等三角形的判定与性质（共2小题）
14．（2021•河池）如图，在Rt△ABC中，∠A＝90°，AB＝4，AC＝3，D，E分别是AB，BC边上的动点，以BD为直径的⊙O交BC于点F．
（1）当AD＝DF时，求证：△CAD≌△CFD；
（2）当△CED是等腰三角形且△DEB是直角三角形时，求AD的长．

【解答】证明：（1）∵BD为⊙O直径，
∴∠DFB＝90°，
在Rt△ACD与Rt△FCD中，
，
∴Rt△ACD≌Rt△FCD（HL），
解：（2）∵△DEB是直角三角形，且∠B＜90°，
∴直角顶点只能是D点和E点，
①若∠EDB＝90°，
如图1，在AB上取点D，使CD平分∠ACB，过D作DE⊥AB交BC于E，
∵CD平分∠ACB，
∴∠ACD＝∠ECD，
∵∠CAB＝∠EDB＝90°，
∴AC∥DE，
∴∠ACD＝∠CDE，
∴∠ECD＝∠CDE，
∴CE＝DE，
此时△ECD为E为顶角顶点的等腰三角形，△DEB是以D为直角顶点的直角三角形，
设CE＝DE＝x，
在直角△ABC中，BC＝＝5，
∴BE＝5﹣x，
∵DE∥AC，
∴△BDE∽△BAC，
∴＝，
∴，
∴x＝，
∴，
∵DE∥AC，
∴，
∴，
∴AD＝，
②若∠DEB＝90°，
如图2，则∠CED＝90°，
∵△CED为等腰三角形，
∴∠ECD＝∠EDC＝45°，
∴可设CE＝DE＝y，
∵tan∠B＝＝，
∴tan∠B＝＝，
∴，
∴BC＝CE+EB＝5，
∴y+＝5，
∴，
∴CE＝DE＝，
∴BD＝＝＝，
∴AD＝AB﹣BD＝4﹣＝，
∴AD的长为或．


15．（2020•河池）（1）如图（1），已知CE与AB交于点E，AC＝BC，∠1＝∠2．求证：△ACE≌△BCE．
（2）如图（2），已知CD的延长线与AB交于点E，AD＝BC，∠3＝∠4．探究AE与BE的数量关系，并说明理由．

【解答】（1）证明：在△ACE和△BCE中，
∵，
∴△ACE≌△BCE（SAS）；
（2）AE＝BE．
理由如下：
在CE上截取CF＝DE，连接BF，

在△ADE和△BCF中，
∵，
∴△ADE≌△BCF（SAS），
∴AE＝BF，∠AED＝∠CFB，
∵∠AED+∠BEF＝180°，∠CFB+∠EFB＝180°，
∴∠BEF＝∠EFB，
∴BE＝BF，
∴AE＝BE．
一十．平行四边形的判定（共1小题）
16．（2022•河池）如图，点A，F，C，D在同一直线上，AB＝DE，AF＝CD，BC＝EF．
（1）求证：∠ACB＝∠DFE；
（2）连接BF，CE，直接判断四边形BFEC的形状．

【解答】（1）证明：∵AF＝CD，
∴AF+CF＝CD+CF，
即AC＝DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS），
∴∠ACB＝∠DFE；
（2）解：如图，四边形BFEC是平行四边形，理由如下：
由（1）可知，∠ACB＝∠DFE，
∴BC∥EF，
又∵BC＝EF，
∴四边形BFEC是平行四边形．

一十一．切线的判定与性质（共1小题）
17．（2020•河池）如图，AB是⊙O的直径，AB＝6，OC⊥AB，OC＝5，BC与⊙O交于点D，点E是的中点，EF∥BC，交OC的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）CG∥OD，交AB于点G，求CG的长．

【解答】证明：（1）连接OE，交BD于H，

∵点E是的中点，OE是半径，
∴OE⊥BD，BH＝DH，
∵EF∥BC，
∴OE⊥EF，
又∵OE是半径，
∴EF是⊙O的切线；
（2）∵AB是⊙O的直径，AB＝6，OC⊥AB，
∴OB＝3，
∴BC＝＝＝，
∵S△OBC＝×OB×OC＝×BC×OH，
∴OH＝＝，
∵cos∠OBC＝，
∴＝，
∴BH＝，
∴BD＝2BH＝，
∵CG∥OD，
∴，
∴＝，
∴CG＝．
一十二．圆的综合题（共1小题）
18．（2022•河池）如图，AB是⊙O的直径，E为⊙O上的一点，∠ABE的平分线交⊙O于点C，过点C的直线交BA的延长线于点P，交BE的延长线于点D．且∠PCA＝∠CBD．
（1）求证：PC为⊙O的切线；
（2）若PC＝2BO，PB＝12，求⊙O的半径及BE的长．

【解答】（1）证明：连接OC，
∵BC平分∠ABE，
∴∠ABC＝∠CBD，
∵OC＝OB，
∴∠ABC＝∠OCB，
∵∠PCA＝∠CBD，
∴∠PCA＝∠OCB，
∵AB是直径，
∴∠ACB＝90°，
∴∠ACO+∠OCB＝90°，
∴∠PCA+∠ACO＝90°，
∴∠PCO＝90°，
∴OC⊥PC，
∵OC是半径，
∴PC是⊙O的切线；

（2）解：连接AE，设OB＝OC＝r，
∵PC＝2OB，
∴PC＝2r，
∴OP＝＝＝3r，
∵PB＝12，
∴4r＝12，
∴r＝3，
由（1）可知，∠OCB＝∠CBD，
∴OC∥BD，
∴＝，∠D＝∠PCO＝90°，
∴＝，
∴BD＝4，
∵AB是直径，
∴∠AEB＝90°，
∴∠AEB＝∠D＝90°，
∴AE∥PD，
∴＝，
∴＝，
∴BE＝2．

一十三．作图—应用与设计作图（共1小题）
19．（2021•河池）如图，∠CAD是△ABC的外角．
（1）尺规作图：作∠CAD的平分线AE（不写作法，保留作图痕迹，用黑色墨水笔将痕迹加黑）；
（2）若AE∥BC，求证：AB＝AC．

【解答】（1）解：如图，射线AE即为所求．


（2）证明：∵AE平分∠CAD，
∴∠EAD＝∠EAC，
∵AE∥BC，
∴∠B＝∠EAD，∠C＝∠EAC，
∴∠B＝∠C，
∴AB＝AC．
一十四．作图-位似变换（共1小题）
20．（2022•河池）如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．
（1）画出与△ABC关于y轴对称的△A1B1C1；
（2）以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2：1，并写出点B2的坐标．

【解答】解：（1）如图，△A1B1C1为所作；
（2）如图，△A2B2C2为所作，点B2的坐标为（﹣4，﹣6）；

一十五．解直角三角形的应用-仰角俯角问题（共2小题）
21．（2022•河池）如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度（结果保留整数．参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65）．

【解答】解：如图，过点C作CE⊥AB，垂足为E，
由题意得，CD＝36m，∠BCE＝45°，∠ACE＝33°，
在Rt△BCE中，∠BCE＝45°，
∴BE＝CE＝CD＝36m，
在Rt△ACE中，∠ACE＝33°，CE＝36m，
∴AE＝CE•tan33°≈23.4（m），
∴AB＝AE+BE＝36+23.4＝59.4≈59（m），
答：居民楼AB的高度约为59m．

22．（2021•河池）如图，小明同学在民族广场A处放风筝，风筝位于B处，风筝线AB长为100m，从A处看风筝的仰角为30°，小明的父母从C处看风筝的仰角为50°．
（1）风筝离地面多少m？
（2）A、C相距多少m？
（结果保留小数点后一位，参考数据：sin30°＝0.5，cos30°≈0.8660，tan30°≈0.5774，sin50°≈0.7760，cos50°≈0.6428，tan50°≈1.1918）

【解答】解：（1）过B作BD⊥AC于D，如图所示：
则∠ADB＝∠CDB＝90°，
∵∠BAD＝30°，
∴BD＝AB＝50（m），
即风筝离地面50m；
（2）由（1）得：BD＝50m，
在Rt△BCD中，∠BCD＝50°，
∵tan∠BCD＝＝tan50°≈1.1918，
∴CD≈＝≈41.95（m），
在Rt△ABD中，∠BAD＝30°，
∵tan∠BAD＝＝tan30°≈0.5774，
∴AD≈≈86.60（m），
∴AC＝AD+CD≈41.95+86.60≈128.6（m），
即A、C相距约128.6m．

一十六．扇形统计图（共1小题）
23．（2020•河池）某校举行了主题为“防溺水，保安全”的知识竞赛活动．赛后随机抽取了50名参赛学生的成绩进行相关统计，整理得尚未完整的频数分布表和扇形统计图．现累计了40名参赛学生的成绩，余下10名参赛学生的成绩尚未累计，这10名学生成绩如下（单位：分）：75，63，76，87，69，78，82，75，63，71．
频数分布表
组别
分数段
划记
频数
A
60＜x≤70
正　　
　8　
B
70＜x≤80
正正　　
　15　
C
80＜x≤90
正正正正　　
　22　
D
90＜x≤100
正　　
　5　
（1）在频数分布表中补全各组划记和频数；
（2）求扇形统计图中B组所对应的圆心角的度数；
（3）该校有2000名学生参加此次知识竞赛，估计成绩在80＜x≤100的学生有多少人？

【解答】解：（1）用“划记”统计10名学生的成绩，并统计频数填入表格；

故答案为：8，15，22，5；
（2）360°×＝108°，
答：扇形统计图中B组所对应的圆心角的度数为108°；
（3）2000×＝1080（人），
答：该校2000名学生中，成绩在80＜x≤100的有1080人．
一十七．条形统计图（共1小题）
24．（2021•河池）为了解本校九年级学生的体质健康情况，李老师随机抽取35名学生进行了一次体质健康测试，根据测试成绩制成统计图表．
组别
分数段
人数
A
x＜60
2
B
60≤x＜75
5
C
75≤x＜90
a
D
x≥90
12
请根据上述信息解答下列问题：
（1）本次调查属于 　抽样　调查，样本容量是 　35　；
（2）表中的a＝　16　，样本数据的中位数位于 　C　组；
（3）补全条形统计图；
（4）该校九年级学生有980人，估计该校九年级学生体质健康测试成绩在D组的有多少人？

【解答】解：（1）本次调查属于抽样调查，样本容量是 35，
故答案为：抽样，35；
（2）a＝35﹣2﹣5﹣12＝16，
根据中位数的定义得，样本数据的中位数位于C组，
故答案为：16，C；
（3）由（2）得，C组的人数为16，
补全条形统计图如下：

（4）980×＝336（人），
答：估计该校九年级学生体质健康测试成绩在D组的有336人．
一十八．列表法与树状图法（共1小题）
25．（2022•河池）为喜迎中国共产党第二十次全国代表大会的召开，红星中学举行党史知识竞赛．团委随机抽取了部分学生的成绩作为样本，把成绩按达标，良好，优秀，优异四个等级分别进行统计，并将所得数据绘制成如下不完整的统计图．

请根据图中提供的信息，解答下列问题：
（1）本次调查的样本容量是 　50　，圆心角β＝　144　度；
（2）补全条形统计图；
（3）已知红星中学共有1200名学生，估计此次竞赛该校获优异等级的学生人数为多少？
（4）若在这次竞赛中有A，B，C，D四人成绩均为满分，现从中抽取2人代表学校参加县级比赛．请用列表或画树状图的方法求出恰好抽到A，C两人同时参赛的概率．
【解答】解：（1）本次调查的样本容量是：10÷20%＝50，
则圆心角β＝360°×＝144°，
故答案为：50，144；
（2）成绩优秀的人数为：50﹣2﹣10﹣20＝18（人），
补全条形统计图如下：

（3）1200×＝480（人），
答：估计此次竞赛该校获优异等级的学生人数为480人；
（4）画树状图如下：

共有12种等可能的结果，其中恰好抽到A，C两人同时参赛的结果有2种，
∴恰好抽到A，C两人同时参赛的概率为＝．