海南省三年（2020-2022）中考数学真题分类汇编-03解答题

这是一份海南省三年（2020-2022）中考数学真题分类汇编-03解答题，共36页。试卷主要包含了计算，，与y轴交于点C等内容，欢迎下载使用。

海南省三年（2020-2022）中考数学真题分类汇编-03解答题
一．平方差公式（共1小题）
1．（2020•海南）计算：
（1）|﹣8|×2﹣1﹣+（﹣1）2020；
（2）（a+2）（a﹣2）﹣a（a+1）．
二．二次根式的混合运算（共1小题）
2．（2021•海南）（1）计算：23+|﹣3|÷3﹣×5﹣1；
（2）解不等式组并把它的解集在数轴（如图）上表示出来．

三．二元一次方程组的应用（共3小题）
3．（2022•海南）我省某村委会根据“十四五”规划的要求，打造乡村品牌，推销有机黑胡椒和有机白胡椒．已知每千克有机黑胡椒比每千克有机白胡椒的售价便宜10元，购买2千克有机黑胡椒和3千克有机白胡椒需付280元，求每千克有机黑胡椒和每千克有机白胡椒的售价．
4．（2021•海南）为了庆祝中国共产党成立100周年，某校组织了党史知识竞赛，学校购买了若干副乒乓球拍和羽毛球拍对表现优异的班级进行奖励．若购买2副乒乓球拍和1副羽毛球拍共需280元；若购买3副乒乓球拍和2副羽毛球拍共需480元．求1副乒乓球拍和1副羽毛球拍各是多少元？
5．（2020•海南）某村经济合作社决定把22吨竹笋加工后再上市销售，刚开始每天加工3吨，后来在乡村振兴工作队的指导下改进加工方法，每天加工5吨，前后共用6天完成全部加工任务，问该合作社改进加工方法前后各用了多少天？
四．解一元一次不等式组（共1小题）
6．（2022•海南）（1）计算：×3﹣1+23÷|﹣2|；
（2）解不等式组．
五．二次函数综合题（共3小题）
7．（2022•海南）如图1，抛物线y＝ax2+2x+c经过点A（﹣1，0）、C（0，3），并交x轴于另一点B，点P（x，y）在第一象限的抛物线上，AP交直线BC于点D．
（1）求该抛物线的函数表达式；
（2）当点P的坐标为（1，4）时，求四边形BOCP的面积；
（3）点Q在抛物线上，当的值最大且△APQ是直角三角形时，求点Q的横坐标；
（4）如图2，作CG⊥CP，CG交x轴于点G（n，0），点H在射线CP上，且CH＝CG，过GH的中点K作KI∥y轴，交抛物线于点I，连接IH，以IH为边作出如图所示正方形HIMN，当顶点M恰好落在y轴上时，请直接写出点G的坐标．

8．（2021•海南）已知抛物线y＝ax2+x+c与x轴交于A、B两点，与y轴交于C点，且点A的坐标为（﹣1，0）、点C的坐标为（0，3）．
（1）求该抛物线的函数表达式；
（2）如图1，若该抛物线的顶点为P，求△PBC的面积；
（3）如图2，有两动点D、E在△COB的边上运动，速度均为每秒1个单位长度，它们分别从点C和点B同时出发，点D沿折线COB按C→O→B方向向终点B运动，点E沿线段BC按B→C方向向终点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，请解答下列问题：
①当t为何值时，△BDE的面积等于；
②在点D、E运动过程中，该抛物线上存在点F，使得依次连接AD、DF、FE、EA得到的四边形ADFE是平行四边形，请直接写出所有符合条件的点F的坐标．

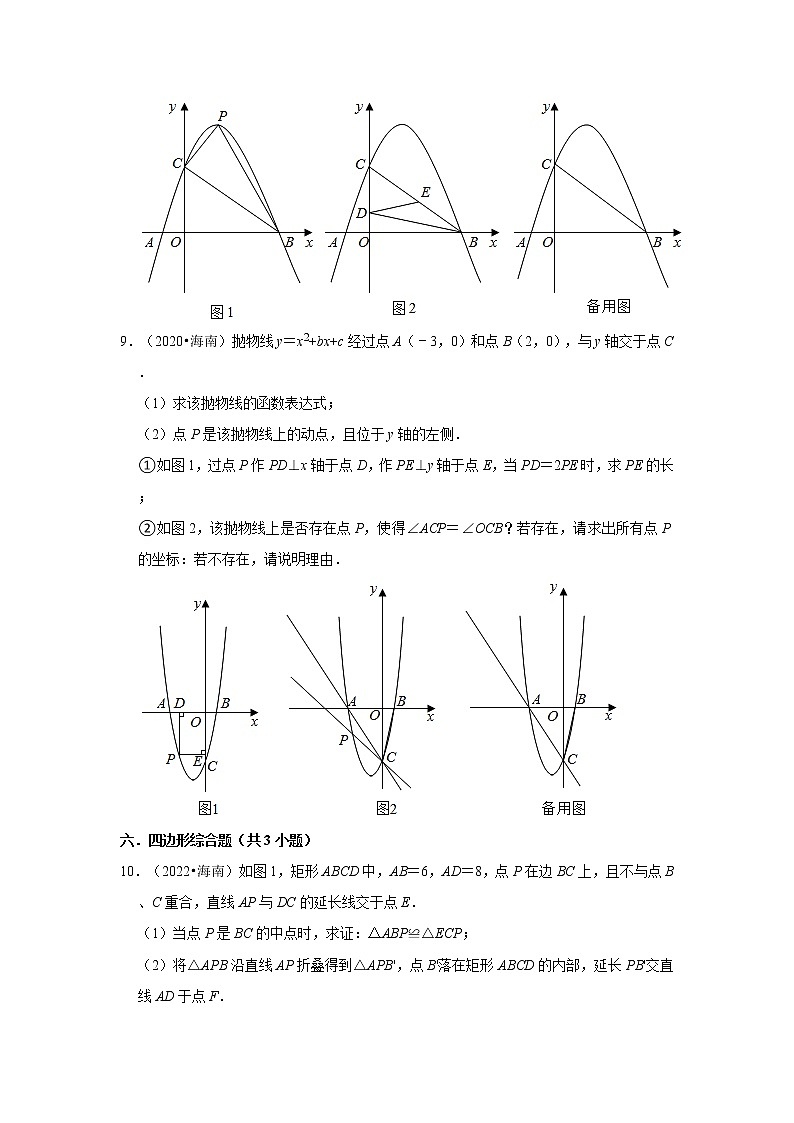
9．（2020•海南）抛物线y＝x2+bx+c经过点A（﹣3，0）和点B（2，0），与y轴交于点C．
（1）求该抛物线的函数表达式；
（2）点P是该抛物线上的动点，且位于y轴的左侧．
①如图1，过点P作PD⊥x轴于点D，作PE⊥y轴于点E，当PD＝2PE时，求PE的长；
②如图2，该抛物线上是否存在点P，使得∠ACP＝∠OCB？若存在，请求出所有点P的坐标：若不存在，请说明理由．

六．四边形综合题（共3小题）
10．（2022•海南）如图1，矩形ABCD中，AB＝6，AD＝8，点P在边BC上，且不与点B、C重合，直线AP与DC的延长线交于点E．
（1）当点P是BC的中点时，求证：△ABP≌△ECP；
（2）将△APB沿直线AP折叠得到△APB'，点B'落在矩形ABCD的内部，延长PB'交直线AD于点F．
①证明FA＝FP，并求出在（1）条件下AF的值；
②连接B'C，求△PCB'周长的最小值；
③如图2，BB'交AE于点H，点G是AE的中点，当∠EAB'＝2∠AEB'时，请判断AB与HG的数量关系，并说明理由．


11．（2021•海南）如图1，在正方形ABCD中，点E是边BC上一点，且点E不与点B、C重合，点F是BA的延长线上一点，且AF＝CE．
（1）求证：△DCE≌△DAF；
（2）如图2，连接EF，交AD于点K，过点D作DH⊥EF，垂足为H，延长DH交BF于点G，连接HB，HC．
①求证：HD＝HB；
②若DK•HC＝，求HE的长．

12．（2020•海南）四边形ABCD是边长为2的正方形，E是AB的中点，连接DE，点F是射线BC上一动点（不与点B重合），连接AF，交DE于点G．
（1）如图1，当点F是BC边的中点时，求证：△ABF≌△DAE；
（2）如图2，当点F与点C重合时，求AG的长；
（3）在点F运动的过程中，当线段BF为何值时，AG＝AE？请说明理由．

七．解直角三角形的应用-仰角俯角问题（共3小题）
13．（2022•海南）无人机在实际生活中应用广泛．如图所示，小明利用无人机测量大楼的高度，无人机在空中P处，测得楼CD楼顶D处的俯角为45°，测得楼AB楼顶A处的俯角为60°．已知楼AB和楼CD之间的距离BC为100米，楼AB的高度为10米，从楼AB的A处测得楼CD的D处的仰角为30°（点A、B、C、D、P在同一平面内）．
（1）填空：∠APD＝　 　度，∠ADC＝　 　度；
（2）求楼CD的高度（结果保留根号）；
（3）求此时无人机距离地面BC的高度．

14．（2021•海南）如图，在某信号塔AB的正前方有一斜坡CD，坡角∠CDK＝30°，斜坡的顶端C与塔底B的距离BC＝8米，小明在斜坡上的点E处测得塔顶A的仰角∠AEN＝60°，CE＝4米，且BC∥NE∥KD，AB⊥BC（点A，B，C，D，E，K，N在同一平面内）．
（1）填空：∠BCD＝　 　度，∠AEC＝　 　度；
（2）求信号塔的高度AB（结果保留根号）．

15．（2020•海南）为了促进海口主城区与江东新区联动发展，文明东越江通道将于今年底竣工通车．某校数学实践活动小组利用无人机测算该越江通道的隧道长度．如图，隧道AB在水平直线上，且无人机和隧道在同一个铅垂面内，无人机在距离隧道450米的高度上水平飞行，到达点P处测得点A的俯角为30°，继续飞行1500米到达点Q处，测得点B的俯角为45°．
（1）填空：∠A＝　 　度，∠B＝　 　度；
（2）求隧道AB的长度（结果精确到1米）．
（参考数据：≈1.414，≈1.732）

八．条形统计图（共1小题）
16．（2021•海南）根据2021年5月11日国务院新闻办公室发布的《第七次全国人口普查公报》，就我国2020年每10万人中，拥有大学（指大专及以上）、高中（含中专）、初中、小学、其他等文化程度的人口（以上各种受教育程度的人包括各类学校的毕业生、肄业生和在校生）受教育情况数据，绘制了条形统计图（图1）和扇形统计图（图2）．

根据统计图提供的信息，解答下列问题：
（1）a＝　 　，b＝　 　；
（2）在第六次全国人口普查中，我国2010年每10万人中拥有大学文化程度的人数约为0.90万，则2020年每10万人中拥有大学文化程度的人数与2010年相比，增长率是 　 　%（精确到0.1%）；
（3）2020年海南省总人口约1008万人，每10万人中拥有大学文化程度的人数比全国每10万人中拥有大学文化程度的人数约少0.16万，那么全省拥有大学文化程度的人数约有 　 　万（精确到1万）．
九．概率公式（共2小题）
17．（2022•海南）某市教育局为了解“双减”政策落实情况，随机抽取几所学校部分初中生进行调查，统计他们平均每天完成作业的时间，并根据调查结果绘制如下不完整的统计图：

请根据图表中提供的信息，解答下面的问题：
（1）在调查活动中，教育局采取的调查方式是 　 　（填写“普查”或“抽样调查”）；
（2）教育局抽取的初中生有 　 　人，扇形统计图中m的值是 　 　；
（3）已知平均每天完成作业时长在“100≤t＜110”分钟的9名初中生中有5名男生和4名女生，若从这9名学生中随机抽取一名进行访谈，且每一名学生被抽到的可能性相同，则恰好抽到男生的概率是 　 　；
（4）若该市共有初中生10000名，则平均每天完成作业时长在“70≤t＜80”分钟的初中生约有 　 　人．
18．（2020•海南）新冠疫情防控期间，全国中小学开展“停课不停学”活动．某市为了解初中生每日线上学习时长t（单位：小时）的情况，在全市范围内随机抽取了n名初中生进行调查，并将所收集的数据分组整理，绘制了如图所示的不完整的频数分布直方图和扇形统计图．

根据图中信息，解答下列问题：
（1）在这次调查活动中，采取的调查方式是　 　（填写“全面调查”或“抽样调查”），n＝　 　；
（2）从该样本中随机抽取一名初中生每日线上学习时长，其恰好在“3≤t＜4”范围的概率是　 　；
（3）若该市有15000名初中生，请你估计该市每日线上学习时长在“4≤t＜5”范围的初中生有　 　名．

参考答案与试题解析
一．平方差公式（共1小题）
1．（2020•海南）计算：
（1）|﹣8|×2﹣1﹣+（﹣1）2020；
（2）（a+2）（a﹣2）﹣a（a+1）．
【解答】解：（1）|﹣8|×2﹣1﹣+（﹣1）2020，
＝8×﹣4+1，
＝4﹣4+1，
＝1；
（2）（a+2）（a﹣2）﹣a（a+1），
＝a2﹣4﹣a2﹣a，
＝﹣4﹣a．
二．二次根式的混合运算（共1小题）
2．（2021•海南）（1）计算：23+|﹣3|÷3﹣×5﹣1；
（2）解不等式组并把它的解集在数轴（如图）上表示出来．

【解答】解：（1）原式＝8+3÷3﹣5×
＝8+1﹣1
＝8；
（2），
解①得x＞﹣3，
解②得x≤2，
所以不等式组的解集为﹣3＜x≤2，
解集在数轴上表示为：

三．二元一次方程组的应用（共3小题）
3．（2022•海南）我省某村委会根据“十四五”规划的要求，打造乡村品牌，推销有机黑胡椒和有机白胡椒．已知每千克有机黑胡椒比每千克有机白胡椒的售价便宜10元，购买2千克有机黑胡椒和3千克有机白胡椒需付280元，求每千克有机黑胡椒和每千克有机白胡椒的售价．
【解答】解：设每千克有机黑胡椒的售价为x元，每千克有机白胡椒的售价为y元，
依题意得：，
解得：．
答：每千克有机黑胡椒的售价为50元，每千克有机白胡椒的售价为60元．
4．（2021•海南）为了庆祝中国共产党成立100周年，某校组织了党史知识竞赛，学校购买了若干副乒乓球拍和羽毛球拍对表现优异的班级进行奖励．若购买2副乒乓球拍和1副羽毛球拍共需280元；若购买3副乒乓球拍和2副羽毛球拍共需480元．求1副乒乓球拍和1副羽毛球拍各是多少元？
【解答】解：设购买1副乒乓球拍x元，1副羽毛球拍y元，根据题意得，
，
解得．
答：购买1副乒乓球拍80元，1副羽毛球拍120元．
5．（2020•海南）某村经济合作社决定把22吨竹笋加工后再上市销售，刚开始每天加工3吨，后来在乡村振兴工作队的指导下改进加工方法，每天加工5吨，前后共用6天完成全部加工任务，问该合作社改进加工方法前后各用了多少天？
【解答】解：设改进加工方法前用了x天，改进加工方法后用了y天，
依题意，得：，
解得：．
答：该合作社改进加工方法前用了4天，改进加工方法后用了2天．
四．解一元一次不等式组（共1小题）
6．（2022•海南）（1）计算：×3﹣1+23÷|﹣2|；
（2）解不等式组．
【解答】解：（1）×3﹣1+23÷|﹣2|
＝3×+8÷2
＝1+4
＝5；
（2），
解不等式①得：x＞﹣1，
解不等式②得：x≤2，
∴原不等式组的解集为：﹣1＜x≤2．
五．二次函数综合题（共3小题）
7．（2022•海南）如图1，抛物线y＝ax2+2x+c经过点A（﹣1，0）、C（0，3），并交x轴于另一点B，点P（x，y）在第一象限的抛物线上，AP交直线BC于点D．
（1）求该抛物线的函数表达式；
（2）当点P的坐标为（1，4）时，求四边形BOCP的面积；
（3）点Q在抛物线上，当的值最大且△APQ是直角三角形时，求点Q的横坐标；
（4）如图2，作CG⊥CP，CG交x轴于点G（n，0），点H在射线CP上，且CH＝CG，过GH的中点K作KI∥y轴，交抛物线于点I，连接IH，以IH为边作出如图所示正方形HIMN，当顶点M恰好落在y轴上时，请直接写出点G的坐标．

【解答】解：（1）由题意得，
，
∴，
∴该抛物线的函数表达式为：y＝﹣x2+2x+3；
（2）当y＝0时，﹣x2+2x+3＝0，
∴x1＝﹣1，x2﹣3，
∴B（3，0），
∵PC2+BC2＝[1+（4﹣3）2]+（32+32）＝20，PB2＝[（3﹣1）2+42]＝20，
∴PC2+BC2＝PB2，
∴∠PCB＝90°，
∴S△PBC＝＝＝3，
∵S△BOC＝＝＝，
∴S四边形BOCP＝S△PBC+S△BOC＝3+＝；
（3）如图1，作PE∥AB交BC的延长线于E，

设P（m，﹣m2+2m+3），
∵B（3，0），C（0，3），
∴直线BC的解析式为：y＝﹣x+3，
由﹣x+3＝﹣m2+2m+3得，
x＝m2﹣2m，
∴PE＝m﹣（m2﹣2m）＝﹣m2+3m，
∵PE∥AB，
∴△PDE∽△ADB，
∴＝＝＝﹣（m﹣）2+，
∴当m＝时，（）最大＝，
当m＝时，y＝﹣（）2+2×+3＝，
∴P（，），
设Q（n，﹣n2+2n+3），
如图2，当∠PAQ＝90°时，过点A作y轴平行线AF，作PF⊥AF于F，作QG⊥AF于G，则△AFP∽△GQA，

∴＝，
∴＝，
∴n＝，
如图3，当∠AQP＝90°时，过QN⊥AB于N，作PM⊥QN于M，可得△ANQ∽△QMP，

∴＝，
∴＝，
可得n1＝1，n2＝，
如图4，当∠APQ＝90°时，作PT⊥AB于T，作QR⊥PT于R，

同理可得：＝，
∴n＝，
综上所述：点Q的横坐标为：或1或或；
（4）如图5，作GL∥y轴，作RC⊥GL于L，作MT⊥KI于K，作HW⊥IK于点W，则△GLC≌△CRH，△ITM≌△HWI．

∴RH＝OG＝﹣n，CR＝GL＝OC＝3，MT＝IW，
∴G（n，0），H（3，3+n），
∴K（，），
∴I（，﹣（）2+n+3+3），
∵TM＝IW，
∴＝（）2+n+6﹣（3+n），
∴（n+3）2+2（n+3）﹣12＝0，
∴n1＝﹣4+，n2＝﹣4﹣（舍去），
∴G（﹣4+，0）．
8．（2021•海南）已知抛物线y＝ax2+x+c与x轴交于A、B两点，与y轴交于C点，且点A的坐标为（﹣1，0）、点C的坐标为（0，3）．
（1）求该抛物线的函数表达式；
（2）如图1，若该抛物线的顶点为P，求△PBC的面积；
（3）如图2，有两动点D、E在△COB的边上运动，速度均为每秒1个单位长度，它们分别从点C和点B同时出发，点D沿折线COB按C→O→B方向向终点B运动，点E沿线段BC按B→C方向向终点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，请解答下列问题：
①当t为何值时，△BDE的面积等于；
②在点D、E运动过程中，该抛物线上存在点F，使得依次连接AD、DF、FE、EA得到的四边形ADFE是平行四边形，请直接写出所有符合条件的点F的坐标．

【解答】解：（1）∵抛物线y＝ax2+x+c经过A（﹣1，0），C（0，3）两点，
∴，
解得，
∴该抛物线的函数表达式为y＝﹣x2+x+3；
（2）∵抛物线y＝﹣x2+x+3＝﹣（x﹣）2+，
∴抛物线的顶点P的坐标为（，），
∵y＝﹣x2+x+3，令y＝0，
解得：x1＝﹣1，x2＝4，
∴B点的坐标为（4，0），OB＝4，
如图，连接OP，

则S△PBC＝S△OPC+S△OPB﹣S△OBC，
＝•OC•|xp|+•OB•|yp|﹣•OB•OC
＝×3×+×4×﹣×4×3
＝+﹣6
＝，
∴△PBC的面积为；
（3）①∵在△OBC中，BC＜OC+OB，
∴当动点E运动到终点C时，另一个动点D也停止运动，
∵OC＝3，OB＝4，
∴在Rt△OBC中，BC＝＝5，
∴0＜t≤5，
当运动时间为t秒时，BE＝t，
如图，
过点E作EN⊥x轴，垂足为N，

则△BEN∽△BCO，
∴＝＝＝，
∴BN＝t，EN＝t，
∴点E的坐标为（4﹣t，t），
下面分两种情形讨论：
Ⅰ、当点D在线段CO上运动时，0＜t＜3，
此时CD＝t，点D的坐标为（0，3﹣t），
∴S△BDE＝S△BOC﹣S△CDE﹣S△BOD
＝BO•CO﹣CD•|xE|﹣OB•OD
＝×4×3﹣×t×（4﹣t）﹣×4×（3﹣t）
＝t2，
当S△BDE＝时，t2＝，
解得t1＝﹣（舍去），t2＝＜3，
∴t＝；
Ⅱ、如图，当点D在线段OB上运动时，3≤t≤5，BD＝7﹣t，

∴S△BDE＝BD•EN，
＝×（7﹣t）×t
＝﹣t2+t，
当S△BDE＝时，
﹣t2+t＝，
解得t3＝，t4＝＜3，
又∵3≤t≤5，
∴t＝，
综上所述，当t＝或t＝时，S△BDE＝；
②当点D在线段OC上，过点E作EH∥x轴，过点F作FH⊥EH于H，

∵四边形ADFE是平行四边形，
∴AD＝EF，AD∥EF，
∴∠ADF+∠DFE＝180°，
∵CO∥FH，
∴∠ODF+∠DFH＝180°，
∴∠ADO＝∠EFH，
又∵∠AOD＝∠EHF，
∴△ADO≌△EFH（AAS），
∴AO＝EH＝1，FH＝DO＝3﹣t，
∵点E的坐标为（4﹣t，t），
∴点F（5﹣t，t+3﹣t），
∴t+3﹣t＝﹣（5﹣t）2+（5﹣t）+3；
解得：t1＝，t2＝（不合题意舍去），
∴F坐标为（，），
当点D在线段OB上，过点E作EQ⊥AB于Q，过点F作FM⊥AB于M，

∵四边形ADFE是平行四边形，
∴AD＝EF，AD∥EF，
∴∠EAQ＝∠FDM，
又∵∠AQE＝∠DMF＝90°，
∴△AEQ≌△DFM（AAS），
∴DM＝AQ，EQ＝FM，EF＝AD＝t﹣3+1＝t﹣2，
∵点E的坐标为（4﹣t，t），
∴点F（2+t，t），
∴t＝﹣（2+t）2+（2+t）+3；
解得：t3＝﹣30（不合题意舍去），t4＝5，
∴F坐标为（3，3）．
综上所述：F坐标为（，）或（3，3）．
9．（2020•海南）抛物线y＝x2+bx+c经过点A（﹣3，0）和点B（2，0），与y轴交于点C．
（1）求该抛物线的函数表达式；
（2）点P是该抛物线上的动点，且位于y轴的左侧．
①如图1，过点P作PD⊥x轴于点D，作PE⊥y轴于点E，当PD＝2PE时，求PE的长；
②如图2，该抛物线上是否存在点P，使得∠ACP＝∠OCB？若存在，请求出所有点P的坐标：若不存在，请说明理由．

【解答】解：（1）∵抛物线y＝x2+bx+c经过点A（﹣3，0）和点B（2，0），
∴，
解得：，
∴抛物线解析式为：y＝x2+x﹣6；
（2）①设点P（a，a2+a﹣6），
∵点P位于y轴的左侧，
∴a＜0，PE＝﹣a，
∵PD＝2PE，
∴|a2+a﹣6|＝﹣2a，
∴a2+a﹣6＝﹣2a或a2+a﹣6＝2a，
解得：a1＝，a2＝（舍去）或a3＝﹣2，a4＝3（舍去）
∴PE＝2或；
②存在点P，使得∠ACP＝∠OCB，
理由如下，
∵抛物线y＝x2+x﹣6与y轴交于点C，
∴点C（0，﹣6），
∴OC＝6，
∵点B（2，0），点A（﹣3，0），
∴OB＝2，OA＝3，
∴BC＝＝＝2，
AC＝＝＝3，
如图，过点A作AH⊥CP于H，

∵∠AHC＝∠BOC＝90°，∠ACP＝∠BCO，
∴△ACH∽△BCO，
∴，
∴＝，
∴AH＝，HC＝，
设点H（m，n），
∴（）2＝（m+3）2+n2，（）2＝m2+（n+6）2，
∴或，
∴点H（﹣，﹣）或（﹣，），
当H（﹣，﹣）时，
∵点C（0，﹣6），
∴直线HC的解析式为：y＝﹣x﹣6，
∴x2+x﹣6＝﹣x﹣6，
解得：x1＝﹣2，x2＝0（舍去），
∴点P的坐标（﹣2，﹣4）；
当H（﹣，）时，
∵点C（0，﹣6），
∴直线HC的解析式为：y＝﹣7x﹣6，
∴x2+x﹣6＝﹣7x﹣6，
解得：x1＝﹣8，x2＝0（舍去），
∴点P的坐标（﹣8，50）；
综上所述：点P坐标为（﹣2，﹣4）或（﹣8，50）．
六．四边形综合题（共3小题）
10．（2022•海南）如图1，矩形ABCD中，AB＝6，AD＝8，点P在边BC上，且不与点B、C重合，直线AP与DC的延长线交于点E．
（1）当点P是BC的中点时，求证：△ABP≌△ECP；
（2）将△APB沿直线AP折叠得到△APB'，点B'落在矩形ABCD的内部，延长PB'交直线AD于点F．
①证明FA＝FP，并求出在（1）条件下AF的值；
②连接B'C，求△PCB'周长的最小值；
③如图2，BB'交AE于点H，点G是AE的中点，当∠EAB'＝2∠AEB'时，请判断AB与HG的数量关系，并说明理由．


【解答】（1）证明：∵四边形ABCD是矩形，
∴AB∥CD，
∴∠BAP＝∠E，∠B＝∠BCE，
∵点P是BC的中点，
∴BP＝CP，
∴△ABP≌△ECP（AAS）；
（2）解：①∵四边形ABCD是矩形，
∴AD∥BC，
∴∠APB＝∠FAP，
由折叠得∠APB＝∠APF，
∴∠FAP＝∠APF，
∴FA＝FP，
矩形ABCD中，AB＝6，AD＝8，
∴BC＝AD＝8，
∵点P是BC的中点，
∴BP＝CP＝4，
由折叠得AB′＝AB＝6，PB′＝PB＝4，∠B＝∠AB′P＝∠AB′F＝90°，
设FA＝x，则FP＝x，
∴FB′＝x﹣4，
在Rt△AB′F中，AF2＝B′F2+B′A2，
∴x2＝（x﹣4）2+62，解得x＝，即AF＝；
②由折叠得AB′＝AB＝6，PB′＝PB＝4，
∴△PCB'的周长＝CP+PB′+CB′＝CB+CB′＝8+CB′，

连接B'C，AC，
∵AB′+B′C＞AC，
∴当点B′恰好位于对角线AC上时，CB′+AB′最小，
在Rt△ABC中，AB＝6，BC＝8，
∴AC＝＝10，
∴CB′的最小值＝AC﹣AB′＝4，
∴△PCB'周长的最小值＝8+CB′＝8+4＝12；
③AB与HG的数量关系是AB＝2HG．
理由：如图，

由折叠可知∠1＝∠6，AB'＝AB，BB'⊥AE，
过点B'作B'M∥DE，交AE于点M，
∴AB∥DE，
∴AB∥DE∥B'M，
∴∠l＝∠6＝∠5＝∠AED，
∴AB'＝B'M＝AB，
∴点H是AM中点，
∵∠EAB'＝2∠AEB'，即∠6＝2∠8，
∴∠5＝2∠8．
∵∠5＝∠7+∠8，
∴∠7＝∠8．
∴B'M＝EM．
∴B'M＝EM＝AB'＝AB．
∵点G为AE中点，点H是AM中点，
∴AG＝AE，AH＝AM．
∴HG＝AG﹣AH＝（AE﹣AM）＝EM．
∴HG＝AB．
∴AB＝2HG．
11．（2021•海南）如图1，在正方形ABCD中，点E是边BC上一点，且点E不与点B、C重合，点F是BA的延长线上一点，且AF＝CE．
（1）求证：△DCE≌△DAF；
（2）如图2，连接EF，交AD于点K，过点D作DH⊥EF，垂足为H，延长DH交BF于点G，连接HB，HC．
①求证：HD＝HB；
②若DK•HC＝，求HE的长．

【解答】解：（1）∵四边形ABCD为正方形，
∴CD＝AD，∠DCE＝∠DAF＝90°，
∵CE＝AF，
∴△DCE≌△DAF（SAS）；

（2）①∵△DCE≌△DAF，
∴DE＝DF，∠CDE＝∠ADF，
∴∠FDE＝∠ADF+∠ADE＝∠CDE+∠ADE＝∠ADC＝90°，
∴△DFE为等腰直角三角形，
∵DH⊥EF，
∴点H是EF的中点，
∴DH＝EF，
同理，由HB是Rt△EBF的中线得：HB＝EF，
∴HD＝HB；
②∵四边形ABCD为正方形，
故CD＝CB，
∵HD＝HB，CH＝CH，
∴△DCH≌△BCH（SSS），
∴∠DCH＝∠BCH＝45°，
∵△DEF为等腰直角三角形，
∴∠DFE＝45°，
∴∠HCE＝∠DFK，
∵四边形ABCD为正方形，
∴AD∥BC，
∴∠DKF＝∠HEC，
∴△DKF∽△HEC，
∴，
∴DK•HC＝DF•HE，
在等腰直角三角形DFH中，DF＝HF＝HE，
∴DK•HC＝DF•HE＝HE2＝，
∴HE＝1．
12．（2020•海南）四边形ABCD是边长为2的正方形，E是AB的中点，连接DE，点F是射线BC上一动点（不与点B重合），连接AF，交DE于点G．
（1）如图1，当点F是BC边的中点时，求证：△ABF≌△DAE；
（2）如图2，当点F与点C重合时，求AG的长；
（3）在点F运动的过程中，当线段BF为何值时，AG＝AE？请说明理由．

【解答】（1）证明：∵四边形ABCD是正方形，
∴∠B＝∠DAE＝90°，AB＝AD＝BC，
∵点E，F分别是AB、BC的中点，
∴AE＝AB，BF＝BC，
∴AE＝BF，
∴△ABF≌△DAE（SAS）；
（2）在正方形ABCD中，AB∥CD，∠ADC＝90°，AD＝CD＝2，
∴AC＝＝＝2，
∵AB∥CD，
∴△AGE∽△CGD，
∴＝，即＝，
∴AG＝；
（3）当BF＝时，AG＝AE，理由如下：
如图所示，设AF交CD于点M，

若使AG＝AE＝1，则有∠1＝∠2，
∵AB∥CD，
∴∠1＝∠4，
又∵∠2＝∠3，
∴∠3＝∠4，
∴DM＝MG，
在Rt△ADM中，AM2﹣DM2＝AD2，即（DM+1）2﹣DM2＝22，
解得DM＝，
∴CM＝CD﹣DM＝2﹣＝，
∵AB∥CD，
∴△ABF∽△MCF，
∴＝，即＝，
∴BF＝，
故当BF＝时，AG＝AE．
七．解直角三角形的应用-仰角俯角问题（共3小题）
13．（2022•海南）无人机在实际生活中应用广泛．如图所示，小明利用无人机测量大楼的高度，无人机在空中P处，测得楼CD楼顶D处的俯角为45°，测得楼AB楼顶A处的俯角为60°．已知楼AB和楼CD之间的距离BC为100米，楼AB的高度为10米，从楼AB的A处测得楼CD的D处的仰角为30°（点A、B、C、D、P在同一平面内）．
（1）填空：∠APD＝　75　度，∠ADC＝　60　度；
（2）求楼CD的高度（结果保留根号）；
（3）求此时无人机距离地面BC的高度．

【解答】解：（1）∵∠MPA＝60°，∠NPD＝45°，
∴∠APD＝180°﹣∠MPA﹣∠NPD＝75°．
过点A作AE⊥CD于点E．

则∠DAE＝30°，
∴∠ADC＝180°﹣90°﹣30°＝60°．
故答案为：75；60．
（2）由题意可得AE＝BC＝100米，EC＝AB＝10米，
在Rt△AED中，∠DAE＝30°，
tan30°＝，
解得DE＝，
∴CD＝DE+EC＝（+10）米．
∴楼CD的高度为（+10）米．
（3）过点P作PG⊥BC于点G，交AE于点F，

则∠PFA＝∠AED＝90°，FG＝AB＝10米，
∵MN∥AE，
∴∠PAF＝∠MPA＝60°，
∵∠ADE＝60°，
∴∠PAF＝∠ADE，
∵∠DAE＝∠30°，
∴∠PAD＝30°，
∵∠APD＝75°，
∴∠ADP＝75°，
∴∠ADP＝∠APD，
则AP＝AD，
∴△APF≌△DAE（AAS），
∴PF＝AE＝100米，
∴PG＝PF+FG＝100+10＝110（米）．
∴此时无人机距离地面BC的高度为110米．
14．（2021•海南）如图，在某信号塔AB的正前方有一斜坡CD，坡角∠CDK＝30°，斜坡的顶端C与塔底B的距离BC＝8米，小明在斜坡上的点E处测得塔顶A的仰角∠AEN＝60°，CE＝4米，且BC∥NE∥KD，AB⊥BC（点A，B，C，D，E，K，N在同一平面内）．
（1）填空：∠BCD＝　150　度，∠AEC＝　30　度；
（2）求信号塔的高度AB（结果保留根号）．

【解答】解：（1）∵BC∥DK，
∴∠BCD+∠D＝180°，
又∵∠D＝30°，
∴∠BCD＝180°﹣30°＝150°，
∵NE∥KD，
∴∠CEN＝∠D＝30°，
又∵∠AEN＝60°，
∴∠ACE＝∠AEN﹣∠CEN＝60°﹣30°＝30°，
故答案为：150，30；
（2）如图，过点C作CG⊥EN，垂足为G，延长AB交EN于点F，
在Rt△CEG中，∵∠CEG＝30°，CE＝4m，
∴CG＝CE＝2（m）＝BF，
∴EG＝CG＝2（m），
设AB＝x，则AF＝（x+2）m，
EF＝BC+EG＝（8+2）m，
在Rt△AEF中，∵∠AEN＝60°，
∴AF＝EF，
即x+2＝（8+2），
x＝（4+8）m，
即信号塔的高度AB为（4+8）m．

15．（2020•海南）为了促进海口主城区与江东新区联动发展，文明东越江通道将于今年底竣工通车．某校数学实践活动小组利用无人机测算该越江通道的隧道长度．如图，隧道AB在水平直线上，且无人机和隧道在同一个铅垂面内，无人机在距离隧道450米的高度上水平飞行，到达点P处测得点A的俯角为30°，继续飞行1500米到达点Q处，测得点B的俯角为45°．
（1）填空：∠A＝　30　度，∠B＝　45　度；
（2）求隧道AB的长度（结果精确到1米）．
（参考数据：≈1.414，≈1.732）

【解答】解：（1）∵点P处测得点A的俯角为30°，点Q处测得点B的俯角为45°，
∴∠A＝30度，∠B＝45度；
故答案为：30，45；
（2）如图，过点P作PM⊥AB于点M，过点Q作QN⊥AB于点N，
则PM＝QN＝450（米），MN＝PQ＝1500（米），

在Rt△APM中，∵tanA＝，
∴AM＝＝＝450（米），
在Rt△QNB中，∵tanB＝，
∴NB＝＝＝450（米），
∴AB＝AM+MN+NB＝450+1500+450≈2729（米）．
答：隧道AB的长度约为2729米．
八．条形统计图（共1小题）
16．（2021•海南）根据2021年5月11日国务院新闻办公室发布的《第七次全国人口普查公报》，就我国2020年每10万人中，拥有大学（指大专及以上）、高中（含中专）、初中、小学、其他等文化程度的人口（以上各种受教育程度的人包括各类学校的毕业生、肄业生和在校生）受教育情况数据，绘制了条形统计图（图1）和扇形统计图（图2）．

根据统计图提供的信息，解答下列问题：
（1）a＝　3.45　，b＝　1.01　；
（2）在第六次全国人口普查中，我国2010年每10万人中拥有大学文化程度的人数约为0.90万，则2020年每10万人中拥有大学文化程度的人数与2010年相比，增长率是 　72.2　%（精确到0.1%）；
（3）2020年海南省总人口约1008万人，每10万人中拥有大学文化程度的人数比全国每10万人中拥有大学文化程度的人数约少0.16万，那么全省拥有大学文化程度的人数约有 　140　万（精确到1万）．
【解答】解：（1）2.48÷24.8%＝10（万人），
a＝10×34.5%＝3.45，
b＝10﹣1.55﹣1.51﹣3.45﹣2.48＝1.01，
故答案为：3.45，1.01；
（2）×100%≈72.2%，
故答案为：72.2；
（3）1008×≈140（万人），
故答案为：140．
九．概率公式（共2小题）
17．（2022•海南）某市教育局为了解“双减”政策落实情况，随机抽取几所学校部分初中生进行调查，统计他们平均每天完成作业的时间，并根据调查结果绘制如下不完整的统计图：

请根据图表中提供的信息，解答下面的问题：
（1）在调查活动中，教育局采取的调查方式是 　抽样调查　（填写“普查”或“抽样调查”）；
（2）教育局抽取的初中生有 　300　人，扇形统计图中m的值是 　30　；
（3）已知平均每天完成作业时长在“100≤t＜110”分钟的9名初中生中有5名男生和4名女生，若从这9名学生中随机抽取一名进行访谈，且每一名学生被抽到的可能性相同，则恰好抽到男生的概率是 　　；
（4）若该市共有初中生10000名，则平均每天完成作业时长在“70≤t＜80”分钟的初中生约有 　3000　人．
【解答】解：（1）∵教育局随机抽取几所学校部分初中生进行调查，
∴教育局采取的调查方式是抽样调查，
故答案为：抽样调查；
（2）45÷15%＝300（人），
1﹣15%﹣3%﹣7%﹣45%＝30%，
故答案为：300，30；
（3）∵所有可能抽到的结果数为9，抽到男生的结果数为5，且每一名学生被抽到的可能性相同，
∴P（抽到男生）＝，
故答案为：；
（4）10000×30%＝3000（人），
故答案为：3000．
18．（2020•海南）新冠疫情防控期间，全国中小学开展“停课不停学”活动．某市为了解初中生每日线上学习时长t（单位：小时）的情况，在全市范围内随机抽取了n名初中生进行调查，并将所收集的数据分组整理，绘制了如图所示的不完整的频数分布直方图和扇形统计图．

根据图中信息，解答下列问题：
（1）在这次调查活动中，采取的调查方式是　抽样调查　（填写“全面调查”或“抽样调查”），n＝　500　；
（2）从该样本中随机抽取一名初中生每日线上学习时长，其恰好在“3≤t＜4”范围的概率是　0.3　；
（3）若该市有15000名初中生，请你估计该市每日线上学习时长在“4≤t＜5”范围的初中生有　1200　名．
【解答】解：（1）在这次调查活动中，采取的调查方式是抽样调查，n＝100÷20%＝500，
故答案为：抽样调查，500；
（2）∵每日线上学习时长在“3≤t＜4”范围的人数为500﹣（50+100+160+40）＝150（人），
∴从该样本中随机抽取一名初中生每日线上学习时长，其恰好在“3≤t＜4”范围的概率是＝0.3；
故答案为：0.3；
（3）估计该市每日线上学习时长在“4≤t＜5”范围的初中生有15000×＝1200（人），
故答案为：1200．