广西梧州三年（2020-2022）中考数学真题分类汇编-02填空题

广西梧州三年（2020-2022）中考数学真题分类汇编-02填空题

一．实数的性质（共1小题）

1．（2022•吉林）﹣的相反数是 　   　．

二．代数式求值（共1小题）

2．（2022•梧州）若x＝1，则3x﹣2＝　   　．

三．提公因式法与公式法的综合运用（共1小题）

3．（2020•梧州）分解因式：2a2﹣8＝　   　．

四．二次根式的加减法（共1小题）

4．（2020•梧州）计算：5﹣3＝　   　．

五．解一元二次方程-因式分解法（共1小题）

5．（2022•梧州）一元二次方程（x﹣2）（x+7）＝0的根是 　   　．

六．根的判别式（共1小题）

6．（2021•梧州）关于x的一元二次方程mx2﹣2x+1＝0有两个不相等的实数根，则实数m的取值范围是 　   　．

七．由实际问题抽象出分式方程（共1小题）

7．（2020•梧州）甲、乙两名工人生产同一种零件，甲每时比乙多生产8个，甲生产168个零件与乙生产144个零件所用的时间相同，设乙每时生产x个零件，根据题意可得方程 　   　．

八．一次函数图象上点的坐标特征（共2小题）

8．（2022•梧州）在平面直角坐标系中，请写出直线y＝2x上的一个点的坐标 　   　．

9．（2021•梧州）如图，直线l的函数表达式为y＝x﹣1，在直线l上顺次取点A1（2，1），A2（3，2），A3（4，3），A4（5，4），…，An（n+1，n），构成形如“”的图形的阴影部分面积分别表示为S1，S2，S3，…，Sn，则S2021＝　   　．

九．一次函数与二元一次方程（组）（共1小题）

10．（2021•梧州）如图，在同一平面直角坐标系中，直线l1：y＝x+与直线l2：y＝kx+3相交于点A，则方程组的解为 　   　．

一十．反比例函数与一次函数的交点问题（共1小题）

11．（2022•梧州）如图，在平面直角坐标系中，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于点A（﹣2，2），B（n，﹣1）．当y1＜y2时，x的取值范围是 　   　．

一十一．三角形中位线定理（共1小题）

12．（2022•梧州）如图，在△ABC中，∠ACB＝90°，点D，E分别是AB，AC边上的中点，连接CD，DE．如果AB＝5m，BC＝3m，那么CD+DE的长是 　   　m．

一十二．正多边形和圆（共3小题）

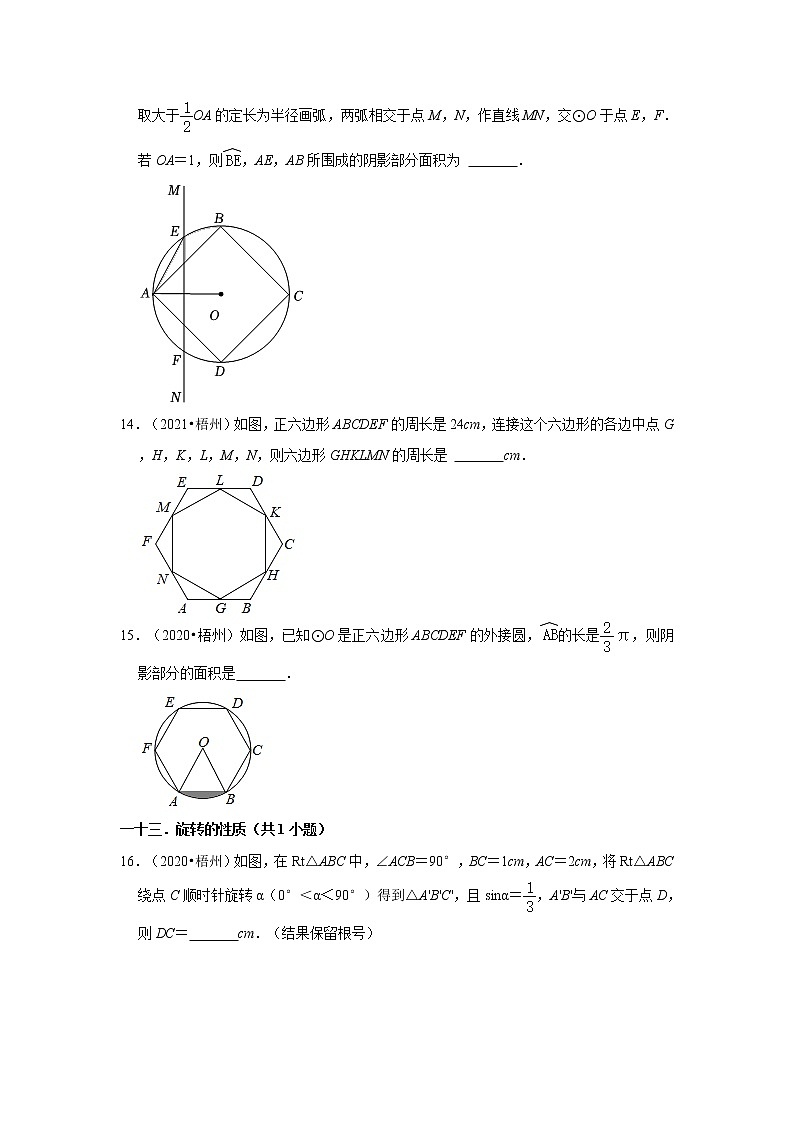
13．（2022•梧州）如图，四边形ABCD是⊙O的内接正四边形，分别以点A，O为圆心，取大于OA的定长为半径画弧，两弧相交于点M，N，作直线MN，交⊙O于点E，F．若OA＝1，则，AE，AB所围成的阴影部分面积为 　   　．

14．（2021•梧州）如图，正六边形ABCDEF的周长是24cm，连接这个六边形的各边中点G，H，K，L，M，N，则六边形GHKLMN的周长是 　   　cm．

15．（2020•梧州）如图，已知⊙O是正六边形ABCDEF的外接圆，的长是，则阴影部分的面积是　   　．

一十三．旋转的性质（共1小题）

16．（2020•梧州）如图，在Rt△ABC中，∠ACB＝90°，BC＝1cm，AC＝2cm，将Rt△ABC绕点C顺时针旋转α（0°＜α＜90°）得到△A'B'C'，且sinα＝，A'B'与AC交于点D，则DC＝　   　cm．（结果保留根号）

一十四．解直角三角形（共1小题）

17．（2020•梧州）如图，已知△ABC的外角∠α＝70°．AB＝2，∠B＝45°，则BC≈　   　．

（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75．结果保留一位小数）

一十五．解直角三角形的应用（共1小题）

18．（2021•梧州）某市跨江大桥即将竣工，某学生做了一个平面示意图（如图），点A到桥的距离是40米，测得∠A＝83°，则大桥BC的长度是 　   　米．（结果精确到1米）（参考数据：sin83°≈0.99，cos83°≈0.12，tan83°≈8.14）

参考答案与试题解析

一．实数的性质（共1小题）

1．（2022•吉林）﹣的相反数是 　　．

【解答】解：﹣的相反数是．

故答案为：．

二．代数式求值（共1小题）

2．（2022•梧州）若x＝1，则3x﹣2＝　1　．

【解答】解：把x＝1代入3x﹣2中，

原式＝3×1﹣2＝1．

故答案为：1．

三．提公因式法与公式法的综合运用（共1小题）

3．（2020•梧州）分解因式：2a2﹣8＝　2（a+2）（a﹣2）　．

【解答】解：2a2﹣8

＝2（a2﹣4），

＝2（a+2）（a﹣2）．

故答案为：2（a+2）（a﹣2）．

四．二次根式的加减法（共1小题）

4．（2020•梧州）计算：5﹣3＝　2　．

【解答】解：原式＝（5﹣3）

＝2，

故答案为：2

五．解一元二次方程-因式分解法（共1小题）

5．（2022•梧州）一元二次方程（x﹣2）（x+7）＝0的根是 　x1＝2，x2＝﹣7　．

【解答】解：（x﹣2）（x+7）＝0，

x﹣2＝0或x+7＝0，

x1＝2，x2＝﹣7，

故答案为：x1＝2，x2＝﹣7．

六．根的判别式（共1小题）

6．（2021•梧州）关于x的一元二次方程mx2﹣2x+1＝0有两个不相等的实数根，则实数m的取值范围是 　m＜1且m≠0　．

【解答】解：由题意得：Δ＞0，

∴（﹣2）2﹣4m×1＞0，

整理得：m＜1．

又∵m≠0，

∴实数m的取值范围是m＜1且m≠0．

故答案是：m＜1且m≠0．

七．由实际问题抽象出分式方程（共1小题）

7．（2020•梧州）甲、乙两名工人生产同一种零件，甲每时比乙多生产8个，甲生产168个零件与乙生产144个零件所用的时间相同，设乙每时生产x个零件，根据题意可得方程 　＝　．

【解答】解：设乙每时生产x个零件，则甲每时生产（x+8）个零件，

根据题意得：＝，

故答案是：＝．

八．一次函数图象上点的坐标特征（共2小题）

8．（2022•梧州）在平面直角坐标系中，请写出直线y＝2x上的一个点的坐标 　（1，2）　．

【解答】解：令x＝1，则y＝2，

∴直线y＝2x经过点（1，2），

∴直线y＝2x上的一个点的坐标为（1，2），

故答案为：（1，2）（答案不唯一）．

9．（2021•梧州）如图，直线l的函数表达式为y＝x﹣1，在直线l上顺次取点A1（2，1），A2（3，2），A3（4，3），A4（5，4），…，An（n+1，n），构成形如“”的图形的阴影部分面积分别表示为S1，S2，S3，…，Sn，则S2021＝　4044　．

【解答】解：由题意得：S1＝2×3﹣2×1＝4＝2×（1+1），

S2＝4×3﹣2×3＝6＝2×（2+1），

S3＝5×4﹣4×3＝8＝2×（3+1），

S4＝6×5﹣5×4＝10＝2×（4+1），

⋯

∴Sn＝2（n+1），

∴S2021＝2×（2021+1）＝4044．

故答案为：4044．

九．一次函数与二元一次方程（组）（共1小题）

10．（2021•梧州）如图，在同一平面直角坐标系中，直线l1：y＝x+与直线l2：y＝kx+3相交于点A，则方程组的解为 　　．

【解答】解：∵直线l1：y＝x+与直线l2：y＝kx+3相交于点A（2，1），

∴关于x、y的方程组的解为，

故答案为：．

一十．反比例函数与一次函数的交点问题（共1小题）

11．（2022•梧州）如图，在平面直角坐标系中，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于点A（﹣2，2），B（n，﹣1）．当y1＜y2时，x的取值范围是 　﹣2＜x＜0或x＞4　．

【解答】解：∵反比例函数y2＝的图象经过点A（﹣2，2），B（n，﹣1），

∴﹣1×n＝（﹣2）×2，

∴n＝4．

∴B（4，﹣1）．

由图象可知：第二象限中点A的右侧部分和第四象限中点B右侧的部分满足y1＜y2，

∴当y1＜y2时，x的取值范围是﹣2＜x＜0或x＞4．

故答案为：﹣2＜x＜0或x＞4．

一十一．三角形中位线定理（共1小题）

12．（2022•梧州）如图，在△ABC中，∠ACB＝90°，点D，E分别是AB，AC边上的中点，连接CD，DE．如果AB＝5m，BC＝3m，那么CD+DE的长是 　4　m．

【解答】解：∵点D，E分别是AB，AC边上的中点，

∴DE是△ABC的中位线，

∴DE＝BC，

∵BC＝3m，

∴DE＝1.5m，

∵∠ACB＝90°，

∴CD＝AB，

∵AB＝5m，

∴CD＝2.5m，

∴CD+DE＝2.5+1.5＝4（m），

故答案为：4．

一十二．正多边形和圆（共3小题）

13．（2022•梧州）如图，四边形ABCD是⊙O的内接正四边形，分别以点A，O为圆心，取大于OA的定长为半径画弧，两弧相交于点M，N，作直线MN，交⊙O于点E，F．若OA＝1，则，AE，AB所围成的阴影部分面积为 　　．

【解答】解：连接OA，

由题意可知，直线MN垂直平分线段OA，

∴EA＝EO，

∵OA＝OE，

∴△AOE为等边三角形，

∴∠AOE＝60°，

∵四边形ABCD是⊙O的内接正四边形，

∴∠AOB＝90°，

∴∠BOE＝30°，

∵S弓形AOE＝S扇形AOE﹣S△AOE，

∴S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB

＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB

＝S扇形AOB﹣S扇形AOE+S△AOE﹣S△AOB

＝S扇形BOE+S△AOE﹣S△AOB

＝+﹣

＝．

故答案为：．

14．（2021•梧州）如图，正六边形ABCDEF的周长是24cm，连接这个六边形的各边中点G，H，K，L，M，N，则六边形GHKLMN的周长是 　12　cm．

【解答】解：设正六边形ABCDEF的中心为O，

连接OG，OB，

∵正六边形ABCDEF的周长是24cm，

∴OB＝AB＝×24＝4（cm），

∴OG＝OB＝2（cm），

∵顺次连接正六边形ABCDEF各边的中点G、H、I、J、K、L得到的六边形为正六边形，

∴NG＝OG＝2cm，

∴六边形GHKLMN的周长是12（cm），

故答案为：12．

15．（2020•梧州）如图，已知⊙O是正六边形ABCDEF的外接圆，的长是，则阴影部分的面积是　﹣　．

【解答】解：∵⊙O是正六边形ABCDEF的外接圆，

∴∠AOB＝＝60°，

∵的长是π，

∴＝π，

∴OA＝2，

∴S扇形OAB＝＝，

过O作OH⊥AB于H，

∵OA＝OB，

∴△OAB是等边三角形，

∴AB＝OA＝2，∠AOH＝∠AOB＝30°，

∴AH＝AB＝1，

∴OH＝＝，

∴S△OAB＝AB•OH＝，

∴S阴影＝S扇形OAB﹣S△OAB＝﹣，

故答案为：﹣．

一十三．旋转的性质（共1小题）

16．（2020•梧州）如图，在Rt△ABC中，∠ACB＝90°，BC＝1cm，AC＝2cm，将Rt△ABC绕点C顺时针旋转α（0°＜α＜90°）得到△A'B'C'，且sinα＝，A'B'与AC交于点D，则DC＝　（3﹣3）　cm．（结果保留根号）

【解答】解：如图，过点D作DH⊥A'C于H，

∵将Rt△ABC绕点C顺时针旋转α（0°＜α＜90°）得到△A'B'C'，

∴∠A＝∠A'，∠ACA'＝∠BCB'＝α，A'C＝AC＝2（cm），

∴sin∠A'CA＝＝，tanA'＝tanA＝，

∴CD＝3DH，A'H＝2DH，

∴CH＝＝2DH，

∵A'H+CH＝A'C，

∴DH＝（﹣1）（cm），

∴DC＝（3﹣3）（cm），

故答案为：（3﹣3）．

一十四．解直角三角形（共1小题）

17．（2020•梧州）如图，已知△ABC的外角∠α＝70°．AB＝2，∠B＝45°，则BC≈　1.3　．

（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75．结果保留一位小数）

【解答】解：过点A作AD⊥BC，交BC的延长线于点D．

∵AD⊥BC，∠B＝45°，

∴BD＝AD．

∴△ABD为等腰直角三角形．

∵AB＝2，

∴AD＝BD＝2．

在Rt△ACD中，tan∠α＝，

即CD＝

≈0.73．

∴BC＝BD﹣CD

＝2﹣0.73

＝1.27

≈1.3．

故答案为：1.3．

一十五．解直角三角形的应用（共1小题）

18．（2021•梧州）某市跨江大桥即将竣工，某学生做了一个平面示意图（如图），点A到桥的距离是40米，测得∠A＝83°，则大桥BC的长度是 　326　米．（结果精确到1米）（参考数据：sin83°≈0.99，cos83°≈0.12，tan83°≈8.14）

【解答】解：由题意，在Rt△ABC中，

∵AC＝40米，∠A＝83°，tanA＝，

∴BC＝tanA•AC

≈8.14×40

＝325.6

≈326（米）．

故答案为：326．