高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用教案配套ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用教案配套ppt课件，共32页。PPT课件主要包含了复习回顾，四大金刚，几何中，向量中，思考探新，基点原点，求平面的法向量，巩固练习，知识点，课堂小结等内容，欢迎下载使用。

1.空间向量运算的坐标表示
2.空间向量中平行、垂直的向量坐标之间的关系.
3.空间中两点间的距离公式和空间两向量夹角余弦值的计算公式.
我们已经把向量由平面推广到空间，并利用空间向量解决了一些有关空间位置关系和度量的问题.我们发现，建立空间向量与几何要素的对应关系是利用空间向量解决几何问题的关键.
点、线、面是空间的基本图形，点、线段、平面图形是组成空间几何体的基本元素.因此，为了用空间向量研究立体几何问题，首先要用向量表示空间中的点、线、面.
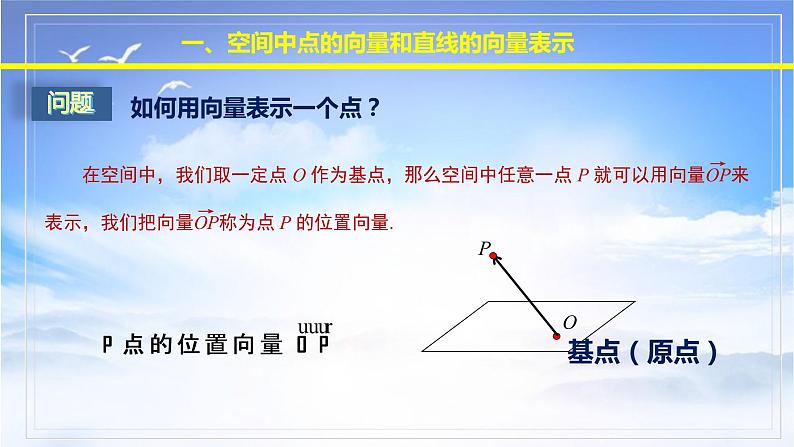
空间中给定一个点A和一个方向就能唯一确定一条直线l
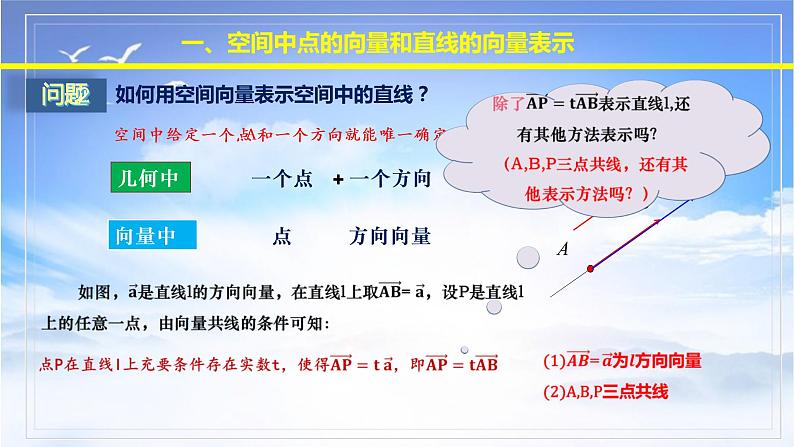
一、空间中点的向量和直线的向量表示
(2)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t.使 .
(3)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t，使 .
2.空间任意直线都可以由直线上一点及直线的方向向量唯一确定.
注意点：(1)空间中，一个向量成为直线l的方向向量，必须具备以下两个条件： ①是非零向量；②向量所在的直线与l平行或重合.
(2)与直线l平行的任意非零向量a都是直线的方向向量，且直线l的方向向量有无数个.
例1 已知直线l的一个方向向量m＝(2，－1,3),且直线l过A(0，y,3)和B(－1,2，z)两点,则y－z 等于( )
解 ∵A(0，y,3)和B(－1,2，z)，
∵直线l的一个方向向量为m＝(2，－1,3) ，
例2 在如图所示的坐标系中，ABCD－A1B1C1D1为正方体，棱长为1，则直线DD1的一个方向向量为________，直线BC1的一个方向向量为__________________.
故直线DD1的一个方向向量为(0,0,1)；
故直线BC1的一个方向向量为(0,1,1).
(0,1,1)(答案不唯一)
【悟】理解直线方向向量的概念
(1)直线上任意两个不同的点都可构成直线的方向向量.
(2)直线的方向向量不唯一.
【练1】(多选)若M(1,0，－1)，N(2,1,2)在直线l上，则直线 l 的一个方向向量是（ ） A.(2,2,6) B.(1,1,3) C.(3,1,1) D.(－3,0,1)
故向量(1,1,3)，(2,2,6)都是直线l的一个方向向量.
解 设B点坐标为 (x，y，z)，
即 (x－2，y＋1，z－7)＝λ(8,9，－12)，
所以x＝18，y＝17，z＝－17.
二、空间中平面的向量表示
（1）不共线的三点确定一个平面
（2）直线和直线外一点确定一个平面
（3）两条相交直线确定一个平面
（4）两条平行直线确定一个平面
立体几何中确定平面的方法：
这种表示在解决几何问题时有重要作用.
【重要结论】:给定空间一点A和一条直线l，过点A且垂直于直线l的平面是唯一确定的
利用点A和直线l的方向向量来确定平面.
一个平面的法向量有无数条，他们之间的关系是共线的
例3 已知长方体ABCD-­A1B1C1D1中，AB=4，BC=3，CC1 =2，M为AB中点.以D为原点，DA， DC，DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系， （1）求平面BCC1B1的一个法向量; （2）求平面MCA1的一个法向量．
解：(1)因为y轴垂直于平面BCC1B1，所以n1=(0,1,0)是平面BCC1B1的一个法向量.
(2)因为AB=4, BC=3, CC1 =2,M是AB的中点，所以M,C,A的坐标分别为 (3,2,0),(0,4,0),(3,0,2).
令z=3，则x=2，y=3，所以n2=(2,3,3)是平面MCA1的一个法向量.
解 （1）以点A为原点,AD,AB,AS所在的直线分别为x轴、y轴、 z轴,建立如图所示的空间直角坐标系，
∵SA⊥平面ABCD，
(2)∵AD⊥AB，AD⊥SA，AB∩SA＝A，AB，SA⊂平面ABS，∴AD⊥平面SAB，
设平面SCD的法向量是n＝(x，y，z)，
令y＝－1，得x＝2，z＝1，∴n＝(2，－1,1).
∴n＝(2，－1,1)是平面SCD的一个法向量(答案不唯一).
求平面法向量的方法与步骤
(4)所求出向量中的三个坐标不是具体的值而是比例关系，
(1)求平面ABC的法向量时，要选取平面内两不共线向量，
(2)设平面的法向量为n＝(x，y，z)；
(5) 设定一个坐标为常数(常数不能为0)便可得到平面的一个法向量.
【练2】如图，在四棱锥P－ABCD中，平面PAB⊥平面ABCD，△PAB是边长为1的正三角形， ABCD是菱形，∠ABC＝60°，E是PC的中点，F是AB的中点，试建立恰当的空间直 角坐标系，求平面DEF的一个法向量.
解　如图，连接PF，CF.
.因为PA＝PB，F为AB的中点，所以PF⊥AB
又因为平面PAB⊥平面ABCD，平面PAB∩平面ABCD＝AB，
PF⊂平面PAB，所以PF⊥平面ABCD.
因为AB＝BC，∠ABC＝60°，所以△ABC是等边三角形， 所以CF⊥AB.
以F为坐标原点，BF，CF，PF所在直线分别为x轴，y轴，z轴，建立空间直角坐标系(如图所示).
设平面DEF的一个法向量为m＝(x，y，z)，
1.若A(－1,0,1)，B(1,4,7)在直线l上，则直线l的一个方向向量为（ ） A.(1,2,3) B.(1,3,2) C.(2,1,3) D.(3,2,1)
所以(1,2,3)是直线l的一个方向向量.
2.若n＝(2，－3,1)是平面α的一个法向量，则下列向量中能作为平面α的法向量的是（） A.(0，－3,1) B.(2,0,1) C.(－2，－3,1) D.(－2,3，－1)
解 求与n共线的一个向量.易知(2，－3,1)＝－(－2,3，－1).
3.已知平面α经过点O(0,0,0)，且e＝(1,2，－3)是α的一个法向量，M(x，y，z)是平 面α内任意一点，则x，y，z满足的关系式是______________.
故x＋2y－3z＝0.
4.已知平面α上的两个向量a＝(2,3,1)，b＝(5,6,4)，则平面α的一个法向量为( ) A.(1，－1,1) B.(2，－1,1) C.(－2,1,1) D.(－1,1,1)
解 显然a与b不平行，
令z＝1，得x＝－2，y＝1.所以n＝(－2,1,1).
设平面α的法向量为n＝(x，y，z)，
5.如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD， PD＝DC＝1，E是PC的中点，求平面EDB的一个法向量.
解 如图所示建立空间直角坐标系.
设平面EDB的法向量为n＝(x，y，z)，
取x＝1,则y＝－1，z＝1,故平面EDB的一个法向量为n＝(1，－1,1).
6.如图,在四棱锥P－ABCD中,底面ABCD为平行四边形,∠DAB＝600,AB＝2AD＝2,PD⊥底面ABCD, 且PD＝AD，试建立恰当的空间直角坐标系，求平面PAB的一个法向量.
从而BD2＋AD2＝AB2，故BD⊥AD，
以D为坐标原点，以射线DA，DB，DP为x，y，z轴的正半轴建立空间直角坐标系，
设平面PAB的一个法向量为n＝(x，y，z).
(1)空间点、直线、平面的向量表示.
2.方法归纳：待定系数法.
3.易错点：不理解直线的方向向量和平面法向量的作用和不唯一性.
(2)直线的方向向量.
课本P29 练习1、2、3