高中数学第七章 随机变量及其分布7.1 条件概率与全概率公式教学课件ppt

这是一份高中数学第七章 随机变量及其分布7.1 条件概率与全概率公式教学课件ppt，共21页。PPT课件主要包含了学习目标，概率乘法公式，情景引入，全概率公式，跟踪练习，课堂小结等内容，欢迎下载使用。

1.利用概率的加法公式和乘法公式,归纳得到全概率公式；2.能用全概率公式计算较复杂的概率问题；3.理解前验概率和后验概率；
请同学们准备好导学案！
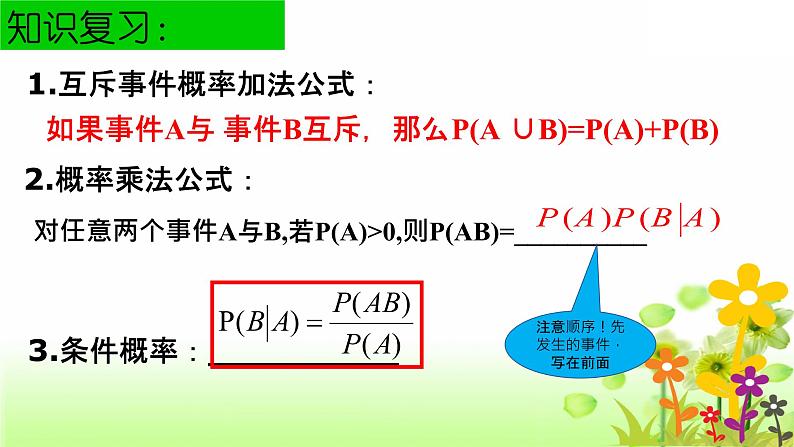
1.互斥事件概率加法公式：
如果事件A与 事件B互斥，那么P(A ∪B)=P(A)+P(B)
对任意两个事件A与B,若P(A)>0,则P(AB)=__________
3.条件概率：_________
注意顺序！先发生的事件，写在前面
2022年第24届冬奥会在北京成功举办！
这场盛会为团结创造全人类更美好的未来，传递着希望与力量！冬奥会的成功举办也包括各个场馆在建设过程中展现出的惊艳世界的“中国速度”和”高质量成果”！
小王是北京冬奥会速滑馆“冰丝带”的一名建设者，一次由于特殊原因，小王上班出发晚了一点时间。已知他从家里出发共有三条路径可以到达 “冰丝带”。 小王选择地铁、私人驾车、公交三种路径的概率分别是0.5,0.3,0.2，而这三条路径拥挤导致迟到的概率分别是0.3,0.4,0.7。请问小王从家到“冰丝带”迟到的概率是多少？
思考1：这个事件分成几步完成？
思考2：“迟到”有几种情况构成？
思考3：“迟到”事件可以分成哪几个（互斥）事件的并事件？（请表述或表示）
小王选择地铁(路径1）、私人驾车(路径2） 、公交(路径3）三种路径的概率分别是0.5,0.3,0.2，而这三条路径拥挤导致迟到的概率分别是0.3,0.4,0.7。请问小王从家到“冰丝带”迟到的概率是多少？
思考1：这个事件分成几步完成？
思考:2：“迟到”有几种情况造成？
思考3：“迟到”事件可以分成哪几个（互斥）事件的并事件？（请表述或表示）
一共两步，第一步是选择路径；第二步是迟到
三种情况：乘坐地铁（路径1）迟到；私人驾车（路径2）迟到；乘坐公交（路径3）迟到
思考3：事件B可以分成哪几个（互斥）事件的并事件？（请表述或表示）
思考4：如何计算P(B)?
思考5：如何计算P(AiB), 以P(A1B)说明?
同理可求P(A2B) P(A3B)
总结：我们把复杂事件B表示为三个互斥事件的并，由概率的加法公式和乘法公式，求得事件B的概率。
小王从家到“冰丝带”,如果有n 条路径，求他迟到的概率P(B)？
二、全概率公式的意义：
例4:某学校有东,西两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6；如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.请完成以下几个问题：
P(B)= P(A1) P(B|A1)+ P(A2) P(B|A2)=0.5×0.6+0.5×0.8=0.7
因此,王同学第2天去A餐厅用餐得概率为0.7.
1.设事件B=“王同学第2天去A餐厅”，事件B有___步构成， 分别是____________2.设出样本空间 _______3.分别计算概率___________________4.用全概率公式计算王同学第2天去A餐厅用餐的概率__________
第一步：第一天选餐厅(A或B)，第二步：第二天选A餐厅
设A1=“第一天选择A餐厅”， A2=“第一天选择B餐厅”
P(A1)=P(A2)=0.5; P(B|A1)=0.6, P(B| A2)=0.8,
三、全概率公式的应用（步骤）：（请同学们进行总结）
1.设出事件(例如可以用B表示）.2.划分样本空间Ω，Ω=A1∪A2∪……∪An, 找到导致事件B发生的原因。3.计算有关事件的概率 ：4.由全概率公式求出概率：
P(A1)，P(A2)…… P(An ) P(B|A1 ) ,P(B| A2)….. P(B|An )
1.从有2个红球和3个篮球的袋子中，每次随机摸出1个球，摸出的球不再放回，求：（1）第1次摸到红球的概率？（2）第2次摸到红球的概率？
例5:有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.(1)任取一个零件,计算它是次品的概率；(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
温馨提示:先计算该次品是第1台机器加工的概率
温馨提示：请对 i=1,i=2,i=3分别计算
问题2：例5中P(Ai), P(Ai|B)的实际意义是什么？
通过这道题深刻感悟数学在实际生活中的应用：
当堂检测：（链接2022.3烟台诊断性考试）