人教版九年级上册21.3 实际问题与一元二次方程优秀综合训练题

这是一份人教版九年级上册21.3 实际问题与一元二次方程优秀综合训练题，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
21.3实际问题与一元二次方程人教版初中数学九年级上册同步练习学校:___________姓名：___________班级：___________考号：___________第I卷（选择题） 一、选择题（本大题共10小题，共30.0分）某蔬菜种植基地年的蔬菜产量为吨，年的蔬菜产量为吨，设每年蔬菜产量的年平均增长率都为，则年平均增长率应满足的方程为(    )A.  B.
C.  D. 如图，是两条互相垂直的街道，且到，的距离都是，现甲从地走向地，乙从地走向地，若两人同时出发且速度都是，则两人之间的距离为时，是甲出发后(    )
 A.  B.  C. 或 D. 或甲、乙两人同驾一辆车出游，各匀速驾驶一半路程，共用小时，到达目的地后，甲对乙说：“我用你所花的时间，可以行驶”乙对甲说：“我用你所花的时间，只能行驶”从他们的交谈中可以判断，乙驾车的时长为(    )A. 小时 B. 小时 C. 小时 D. 小时如图，在中，，，点从点开始沿边向点以的速度移动，点从点开始沿边向点以的速度移动．若、两点同时出发，当点运动到点时，、两点同时停止运动，当的面积是的面积的三分之一时，经过的时间是  (    )A.  B.  C. 或 D. 或有一人患了新型冠状病毒肺炎，经过两轮传染后共有人患了新型冠状病毒肺炎，那么每轮传染中平均一个人传染的人数为(    )A. 人 B. 人 C. 人 D. 人如图，某小区有一块长为米，宽为米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为米，则可以列出关于的方程是(    )
A.  B.
C.  D. 如图，在中，，，，动点，分别从点，同时开始运动．点的速度为，点的速度为，点运动到点停止，点运动到点后停止．经过多长时间，能使的面积为(    )A.  B.  C.  D. 某商品经过两次降价后每件的售价由原来的元降到了元．则平均每次降价的百分率为(    )A.  B.  C.  D. 如图，这是一个三角点阵，从上向下数有无数多行，其中第一行有个点，第二行有个点，第行有个点，前行的点数和不能是以下哪个结果(    )A.
B.
C.
D. 某种衬衣的价格经过连续两次降价后，由每件元降至元，求平均每次降价的百分率．设平均每次降价的百分率为，根据题意可列方程(    )A.  B.
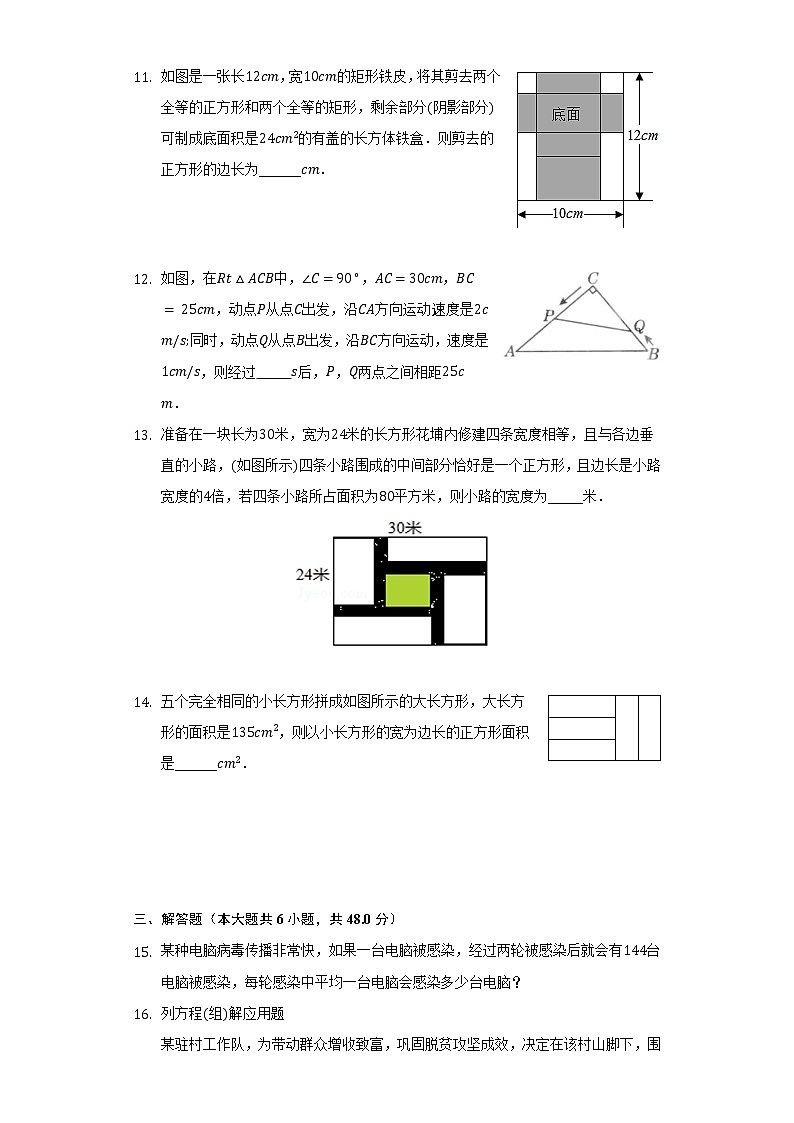
C.  D. 第II卷（非选择题） 二、填空题（本大题共4小题，共12.0分）如图是一张长，宽的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分阴影部分可制成底面积是的有盖的长方体铁盒．则剪去的正方形的边长为______．
 如图，在中，，，，动点从点出发，沿方向运动，速度是同时，动点从点出发，沿方向运动，速度是，则经过          后，，两点之间相距．准备在一块长为米，宽为米的长方形花埔内修建四条宽度相等，且与各边垂直的小路，如图所示四条小路围成的中间部分恰好是一个正方形，且边长是小路宽度的倍，若四条小路所占面积为平方米，则小路的宽度为_____米．
五个完全相同的小长方形拼成如图所示的大长方形，大长方形的面积是，则以小长方形的宽为边长的正方形面积是______．
   三、解答题（本大题共6小题，共48.0分）某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮被感染后就会有台电脑被感染，每轮感染中平均一台电脑会感染多少台电脑？列方程组解应用题
某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为的矩形试验茶园，便于成功后大面积推广．如图所示，茶园一面靠墙，墙长，另外三面用长的篱笆围成，其中一边开有一扇宽的门不包括篱笆求这个茶园的长和宽．
 
某中学计划租用客车送名学生和名教师集体外出活动，每辆客车上至少要有名教师．现有甲、乙两种型号的客车，它们的载客量和租金如表所示．设租车总费用为元，租用甲型客车辆． 甲型客车乙型客车载客量人辆租金元辆共需租______辆客车；
若学校计划租车总费用在元的限额内，求关于的函数解析式，并求出自变量的取值范围；
因燃油价格上涨，甲型客车每辆租金上调元，乙型客车每辆租金上调元，若租车的最低费用是元，求的值．如图，在中，，点从点出发，沿边以的速度向点移动；点从点同时出发，沿边以的速度向点移动．规定其中一个动点到达终点时，另一个动点也随之停止运动．问经过几秒后，，两点的距离是？
某童装专卖店在销售中发现，一款童装每件进价为元，销售价为元时，每天可售出件．为了迎接“六一”儿童节，商店决定采取适当的降价措施，以扩大销售量，增加利润．据测算，每件童装每降价元，平均每天可多售出件．设每件童装降价元．
每天可销售多少件，每件盈利多少元？用含的代数式表示
每件童装降价多少元时，平均每天盈利元．
平均每天盈利能否达到元，请说明理由．某网店第一次用元购进一批医用外科口罩，很快销售一空，第二次又用元购进该医用外科口罩，但这次每盒的进价比第一次进价多元，购进数量则是第一次的倍．
第一次每盒医用外科口罩的进价是多少元？
该网店发现：每盒售价为元时，每星期可卖盒．为了便民利民，该网店决定降价销售，市场调查反映：每降价元，每星期可多卖盒．该网店某星期销售该款口罩获得了元的毛利润，该款口罩每盒成本为第二次的进价，那么该网店这星期销售该款口罩多少盒？毛利润售价进价销售量
答案和解析 1.【答案】 【解析】解：依题意得：．
故选：．
根据该种植基地年及年的蔬菜产量，即可得出关于的一元二次方程，此题得解．
本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
 2.【答案】 【解析】【分析】
本题考查了勾股定理及一元二次方程的应用，解题的关键是能够根据勾股定理列出一元二次方程．
设甲出发后，两人之间的距离为，根据勾股定理得出方程，求出即可．
【解答】
解：设甲出发后，两人之间的距离为，根据勾股定理，得
，
，
解得：或．  3.【答案】 【解析】略
 4.【答案】 【解析】【分析】
本题考查了一元二次方程的应用，设经过秒，的面积是的面积的三分之一，由三角形的面积公式建立方程求出其解即可．
【解答】
解：设经过秒，的面积是的面积的三分之一，
则，，，
由题意，得
，
解得：，．
答：设经过秒或秒，的面积等于面积的．
故选C．  5.【答案】 【解析】【分析】
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．设每轮传染中平均一个人传染的人数为人，则第一轮传染了人，第二轮传染了人，根据经过两轮传染后共有人患了新型冠状病毒肺炎，即可得出关于的一元二次方程，解之取其正值即可得出结论．
【解答】
解：设每轮传染中平均一个人传染的人数为人，则第一轮传染了人，第二轮传染了人，
依题意得：，
整理得：，
解得：，不合题意，舍去，
则每轮传染中平均一个人传染的人数为人．  6.【答案】 【解析】【分析】
本题考查了由实际问题抽象出一元二次方程，利用两块相同的矩形绿地面积之和为米得出等式是解题关键．设人行道的宽度为米，根据矩形绿地的面积之和为米，列出一元二次方程．
【解答】
解：设人行道的宽度为米，根据题意得，
，
化简整理得，．
故选C．  7.【答案】 【解析】【分析】
此题考查借助三角形的面积计算公式来研究图形中的动点问题．设出动点，运动秒，能使的面积为，用分别表示出和的长，利用三角形的面积计算公式即可解答．
【解答】解：设动点，运动后，能使的面积为，
则为，为，由三角形的面积计算公式列方程得，
，
解得，当时，，不合题意，舍去．
动点，运动时，能使的面积为．
故选B．
   8.【答案】 【解析】解：设平均每次降价的百分率为，则有：



，舍
故选：．
设平均每次降价的百分率为，根据题意列出关于的一元二次方程并求解，结合问题的实际意义，对所得的解进行取舍即可．
本题考查了一元二次方程在增长率问题中的应用，根据题意正确列出方程是解题的关键．
 9.【答案】 【解析】【分析】
本题主要考查一元二次方程的应用，图形规律问题，解题的关键是列出前行点数之和的代数式，并求出点数之和分别为、、、时的值．前行的点数之和为，再分别求出该代数式的值分别为、、、时的值即可判断．
【解答】
解：由题意，前行的点数之和为，
若前行的点数之和为，则，
解得或舍，即前行的点数之和为，故A不符合题意；
若前行的点数之和为，则，
解得，不是整数，即不存在前行的点数之和为，故B符合题意；
若前行的点数之和为，则，
解得或舍，即前行的点数之和为，故C不符合题意；
若前行的点数之和为，则，
解得或舍，即前行的点数之和为，故D不符合题意．  10.【答案】 【解析】【分析】
本题主要考查了一元二次方程的应用，一元二次方程应用的关键是根据题意找到等式两边的平衡条件，这种价格问题主要解决价格变化前后的平衡关系，列出方程即可．
设平均每次降价的百分率为，为两次降价的百分率，降至就是方程的平衡条件，列出方程即可．
【解答】
解：设平均每次降价的百分率为，则
，
故选B．  11.【答案】 【解析】解：设底面长为，宽为，正方形的边长为，根据题意得：
，
解得，，
代入中，得：
，
整理得：，
解得或舍去，
答；剪去的正方形的边长为．
故答案为：．
根据题意找到等量关系列出方程组，转化为一元二次方程求解即可．
本题考查了一元二次方程的应用，解决本题的关键是根据题意找到等量关系列出方程组．
 12.【答案】或 【解析】略
 13.【答案】 【解析】【分析】
本题考查了一元二次方程的应用，解题的关键是找到该小路的总的长度，利用矩形的面积公式列出方程并解答．设小路的宽度为米，则小正方形的边长为米，根据小路的横向总长度米和纵向总长度米，结合矩形的面积公式得到：通过解方程求得的值即可．
【解答】
解：设小路的宽度为米，则小正方形的边长为米，
依题意得：
整理得：
解得舍去，．
故答案为：．  14.【答案】 【解析】【分析】
本题考查了一元二次方程的应用，读懂图意，找到等量关系，列出方程是解题的关键．
设小长方形的长为，宽为，根据大长方形的面积公式可得关于的一元二次方程，解方程即可得出结论．
【解答】
解：设小长方形的长为，宽为，
根据题意得：，
解得：或舍去，
则．
所以 
故答案为．  15.【答案】解：设每轮感染中平均一台电脑感染台，
依题意，得：，
解得：，不合题意，舍去．
答：每轮感染中平均一台电脑感染台． 【解析】设每轮感染中平均一台电脑感染台，根据经过两轮被感染后就会有台电脑被感染，即可得出关于的一元二次方程，解之取其正值即可得出结论．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
 16.【答案】解：设茶园垂直于墙的一边长为，则另一边的长度为，根据题意，得
，
整理，得
，
解得，，
当时，，不符合题意舍去；
当时，，符合题意．
答：这个茶园的长和宽分别为、． 【解析】本题考查了一元二次方程的应用，根据数量关系列出方程是解题的关键．设当茶园垂直于墙的一边长为时，则另一边的长度为，根据茶园的面积为，列出方程并解答．
 17.【答案】 【解析】解：如果全部租用甲种客车，则需要辆，
如果全部租用乙种客车，则需要辆，
汽车辆数为整数，且有名教师，每辆汽车上至少要有名教师，
共需租辆汽车．
故答案为：；
设租用辆甲种客车，则租用乙种客车辆，
则租车费用，
，
解得，
为整数，
或或．
故关于的函数解析式是，自变量的取值范围是或或；
依题意有：，
解得，
为整数，
或或．
故的值为或或．
根据题意和表格中的数据可以得到需要租用多少辆客车，本题得以解决；
根据中的结果和表格中的数据可以得到关于的函数解析式，以及自变量的取值范围；
根据租车的最低费用是元，列出不等式可求的值．
本题考查一次函数的应用、一元一次不等式组的应用，一元二次方程的应用，解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．
 18.【答案】解：设经过秒后，，两点的距离是，
根据题意，得，
整理，得，
解得，．
当时，，符合题意，
答：秒或秒后，，两点间的距离等于． 【解析】设经过秒后，，两点的距离是，利用勾股定理列出方程并解答即可．
此题考查的是一元二次方程的应用，根据路程速度时间，表示线段的长度，将问题转化到三角形中，利用勾股定理或者面积关系建立等量关系，是解应用题常用的方法．
 19.【答案】解：设每件童装降价元时，每天可销售件，每件盈利元，
故答案为：，；

根据题意，得：．
解得：，，
扩大销售量，增加利润，
，
答：每件童装降价元，平均每天盈利元；

依题意，可列方程：
，
化简，得，
．
故方程无实数根．
故平均每天销售利润不能达到元． 【解析】根据销售量原销售量因价格下降而增加的数量，每件利润实际售价进价，列式即可；
根据总利润每件利润销售数量，列方程求解可得；
根据每台的盈利销售的件数元，即可列方程，再根据根的判别式求解．
本题主要考查一元二次方程的实际应用，理解题意找到题目蕴含的等量关系是列方程求解的关键．
 20.【答案】解：设第一次每盒医用外科口罩进价元，则第二次进价元，
根据题意，得，
解得，
经检验，是原方程的解，且符合题意，
答：第一次每盒医用外科口罩的进价是元．
设降价元，
第二次进价为元，
根据题意，得，
解得或，
为了便民利民，
，
盒，
答：该网店这星期销售该款口罩盒． 【解析】设第一次每盒医用外科口罩进价元，则第二次进价元，根据第二次购进数量则是第一次的倍列分式方程，求解即可；
设降价元，根据该网店某星期销售该款口罩获得了元的毛利润，列一元二次方程，求解即可．
本题考查了分式方程的应用，一元二次方程的应用等，理解题意并建立合适的等量关系是解题的关键．