北师大版七年级上册第一章 丰富的图形世界1.1 生活中的立体图形教课内容课件ppt

这是一份北师大版七年级上册第一章 丰富的图形世界1.1 生活中的立体图形教课内容课件ppt，共27页。PPT课件主要包含了点动成线，线动成面，面动成体，典例赏析，归纳结论，概括结论，议一议等内容，欢迎下载使用。
1.从实例中认识点、线、面,初步感受点、线、面之间的关系。2.从图形的构成中进一步认识常见几何体的特征。
上一节课我们认识了常见的几何体，并且可以从大量的实物中抽象出这些图形.我们知道世间万物都是由一些基本元素构成的，那么构成这些图形的基本元素是什么呢？
这就是我们本节课要学习的内容.
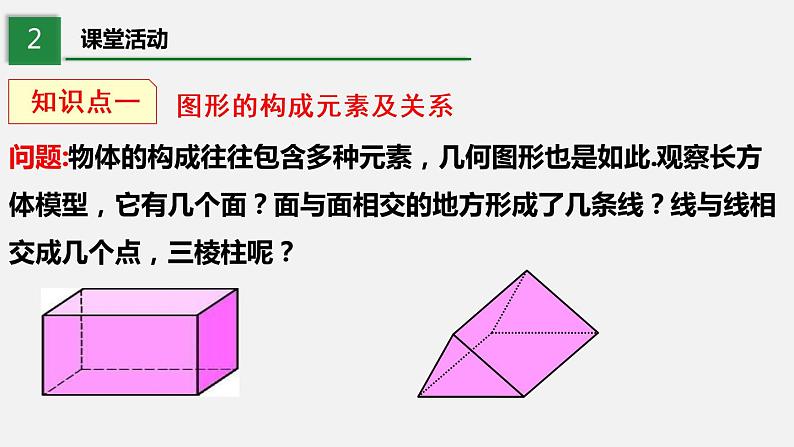
问题:物体的构成往往包含多种元素，几何图形也是如此.观察长方体模型，它有几个面？面与面相交的地方形成了几条线？线与线相交成几个点，三棱柱呢？
观察可知:长方体有____个面，面与面相交的地方形成了 ___ 条线，线与线相交成____个点；三棱柱有____个面,面与面相交的地方形成了__ _条线，线与线相交成____个点．
归纳：图形的构成元素包括____、____、____、____．
方法点拨：在立体图形中，面与面相交得到线，线与线相交得到点.在数面时可先数底面，再数侧面；数棱时，可先数底面与侧面相交的棱，再数侧面与侧面相交的棱；根据棱与棱相交得到的点是顶点来确定顶点个数.
议一议(1)六棱柱是由几个面围成的？圆柱是由几个面围成的？它们都是平的吗?(2)圆柱的侧面和底面相交成几条线？它们是直的还是曲的？(3)六棱柱有几个顶点？经过每个顶点有几条棱？
要点精析：(1)图形是由点、线、面构成的，点是构成图形的基本元素，面与面相交得到线，线与线相交得到点．(2)线有直的和曲的之分，面有平的和曲的之分．
例1.笔尖在纸上快速滑动写出了一个又一个字，这说明了________；车轮旋转时，看起来像一个整体的圆面，这说明了__________；直角三角形绕它的直角边所在的直线旋转一周，形成了一个圆锥，这说明_________．
总结：本题考查图形的构成及其关系，构成图形的要素是点、线、面．重点考查学生的空间想象能力和抽象概括能力．
物体的运动会留下运动轨迹, 这些运动轨迹往往也能抽象成几何图形.如果把笔尖看成一个点,这个点在纸上运动时,形成的图形是什么?动手试一试.
举出生活中能够说明“点动成线”这一结论的例子.
汽车的雨刷在挡风玻璃上画出一个扇面，从几何的角度观察这种现象，你可以得出什么结论？
既然“点动成线，线动成面”，那么请同学们想一想：当面运动时又会形成什么图形？如何验证你的猜想？
1.圆柱可以看做由哪个平面图形旋转得到？球体呢？
2.图中各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到？用线连一连。
总结：一般地，有曲面的几何体都可以由某平面图形旋转得到．将一个平面图形旋转成立体图形需要明确旋转轴和旋转角两个条件．
例2.长和宽分别是6 cm和3 cm的长方形绕它的一边所在直线旋转一周后，得到的几何体的形状是什么？其体积是多少？
解：分两种情况(分类讨论)：(1)当以长方形的宽所在的直线为轴旋转时，如图①，所得几何体为圆柱，其体积为π×62×3＝108π(cm3)．(2)当以长方形的长所在的直线为轴旋转时，如图②，所得几何体仍为圆柱，其体积为π×32×6＝54π(cm3)．综上可知，所得几何体为圆柱，其体积为108πcm3或54π cm3.
例3.一位美术老师在课堂上进行立体模型素描教 学时，把14个棱长为1 dm的正方体摆在课桌上(如图)，然后他把露出的面涂成不同的颜色，则被他涂上颜色的部分的面积为(　　)A．33 dm2　 B．24 dm2C．21 dm2 D．42 dm2
总结：解答此题有两种思路，一是依次求出各层露出的面的面积和；二是将露出的面分成侧面和上表面两部分来求
1. [2022合肥段考]下列几何体中,含有曲面的有 (　　)A.1个 B.2个C.3个 D.4个
　含有曲面的有球、圆柱,共2个.
2. [2022青岛期末]电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,该现象说明(　　)A.点动成线B.线动成面C.面动成体D.以上都不对
3. 新情境[2022上饶期末]元旦假期,小明和小亮相约去上饶市龙潭湖公园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体.请问这个几何体是 (　　)A.圆锥B.圆柱C.球D.正方体
4.[2022济南槐荫区期末]下列立体图形中,不能由某一平面图形绕轴旋转一周得到的是 (　　)
将“半圆”绕着其直径所在的直线旋转一周,所形成的几何体是“球”;由于正方体的六个面都是“平面”,因此不可能由某一平面图形绕轴旋转一周得到;将“长方形”绕着一条边所在的直线旋转一周,所形成的几何体是“圆柱”;将“直角三角形”绕着一条直角边所在的直线旋转一周,所形成的几何体是“圆锥”.
5. [2022吉林期末]下列四个平面图形绕虚线旋转一周,可以得到圆柱的是 (　　)
A项中的图形绕虚线旋转一周得到半球;B项中的图形绕虚线旋转一周得到圆台;C项中的图形绕虚线旋转一周得到圆锥;D项中的图形绕虚线旋转一周得到圆柱.
6.[2022襄阳期末]将下列平面图形绕轴旋转一周,可得到如图所示的立体图形的是 (　　)
A项中的图形绕轴旋转一周,可得到圆柱,故此项不符合题意;B项中的图形绕轴旋转一周,可得到球,故此项不符合题意;C项中的图形绕轴旋转一周,可得到一个中间空心的几何体,故此项不符合题意.
7.如图,大长方形的长为8 cm,宽为6 cm,小长方形的长为4 cm,宽为3 cm,以长边中点连线(图中的虚线)为轴,将图中的阴影部分旋转一周得到的几何体的表面积为　　　　cm2.(结果保留π) 
10.92π　两个长方形旋转后形成两个圆柱,根据题意,求出大圆柱的侧面积和小圆柱的侧面积,再加上大圆柱的上、下两底面圆的面积,即可得出所求几何体的表面积.由题意可得,大圆柱的侧面积为π×8×6=48π(cm2),小圆柱的侧面积为π×4×3=12π(cm2),大圆柱上、下两底面圆的面积和为2π×42=32π(cm2),所以该几何体的表面积为48π+12π+32π=92π(cm2).
1.一个正n 棱柱，它有18条棱，一条侧棱长为10cm，一条底面边长为5cm.问（1）这是几棱柱？（2）此棱柱的侧面积是多少？
解：因为是棱柱，有18条棱，所以n＝18/3＝6，即为6棱柱.
所以底面周长为5*6＝30(cm).所以此棱柱的侧面积是30*10＝300cm2.
因为是正6棱柱即底面为正六面形，