

所属成套资源:多地区中考数学真题按题型知识点分层分类汇编
湖南省娄底市三年(2020-2022)中考数学真题分类汇编-03解答题
展开
这是一份湖南省娄底市三年(2020-2022)中考数学真题分类汇编-03解答题,共39页。试卷主要包含了﹣1+|1﹣|﹣2sin60°,﹣1,﹣1﹣2cs45°等内容,欢迎下载使用。
湖南省娄底市三年(2020-2022)中考数学真题分类汇编-03解答题
一.实数的运算(共2小题)
1.(2022•娄底)计算:(2022﹣π)0+()﹣1+|1﹣|﹣2sin60°.
2.(2020•娄底)计算:|﹣1|﹣3tan30°+(3.14﹣π)0+()﹣1.
二.分式的化简求值(共3小题)
3.(2022•娄底)先化简,再求值:(x+2+)÷,其中x是满足条件x≤2的合适的非负整数.
4.(2021•娄底)先化简,再求值:•(1﹣),其中x是1、2、3中的一个合适的数.
5.(2020•娄底)先化简(﹣)÷,然后从﹣3,0,1,3中选一个合适的数代入求值.
三.分母有理化(共1小题)
6.(2021•娄底)计算:(﹣π)0++()﹣1﹣2cos45°.
四.二元一次方程组的应用(共2小题)
7.(2022•娄底)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4mg,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为62mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克?
8.(2021•娄底)为了庆祝中国共产党建党一百周年,某校举行“礼赞百年,奋斗有我”演讲比赛,准备购买甲、乙两种纪念品奖励在活动中表现优秀的学生.已知购买1个甲种纪念品和2个乙种纪念品共需20元,购买2个甲种纪念品和5个乙种纪念品共需45元.
(1)求购买一个甲种纪念品和一个乙种纪念品各需多少元;
(2)若要购买这两种纪念品共100个,投入资金不少于766元又不多于800元,问有多少种购买方案?并求出所花资金的最小值.
五.一元一次不等式的应用(共1小题)
9.(2020•娄底)为了预防新冠肺炎疫情的发生,学校免费为师生提供防疫物品.某校花7200元购进洗手液与84消毒液共400瓶,已知洗手液的价格是25元/瓶,84消毒液的价格是15元/瓶.
求:(1)该校购进洗手液和84消毒液各多少瓶?
(2)若购买洗手液和84消毒液共150瓶,总费用不超过2500元,请问最多能购买洗手液多少瓶?
六.二次函数综合题(共3小题)
10.(2022•娄底)如图,抛物线y=x2﹣2x﹣6与x轴相交于点A、点B,与y轴相交于点C.
(1)请直接写出点A,B,C的坐标;
(2)点P(m,n)(0<m<6)在抛物线上,当m取何值时,△PBC的面积最大?并求出△PBC面积的最大值.
(3)点F是抛物线上的动点,作FE∥AC交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.
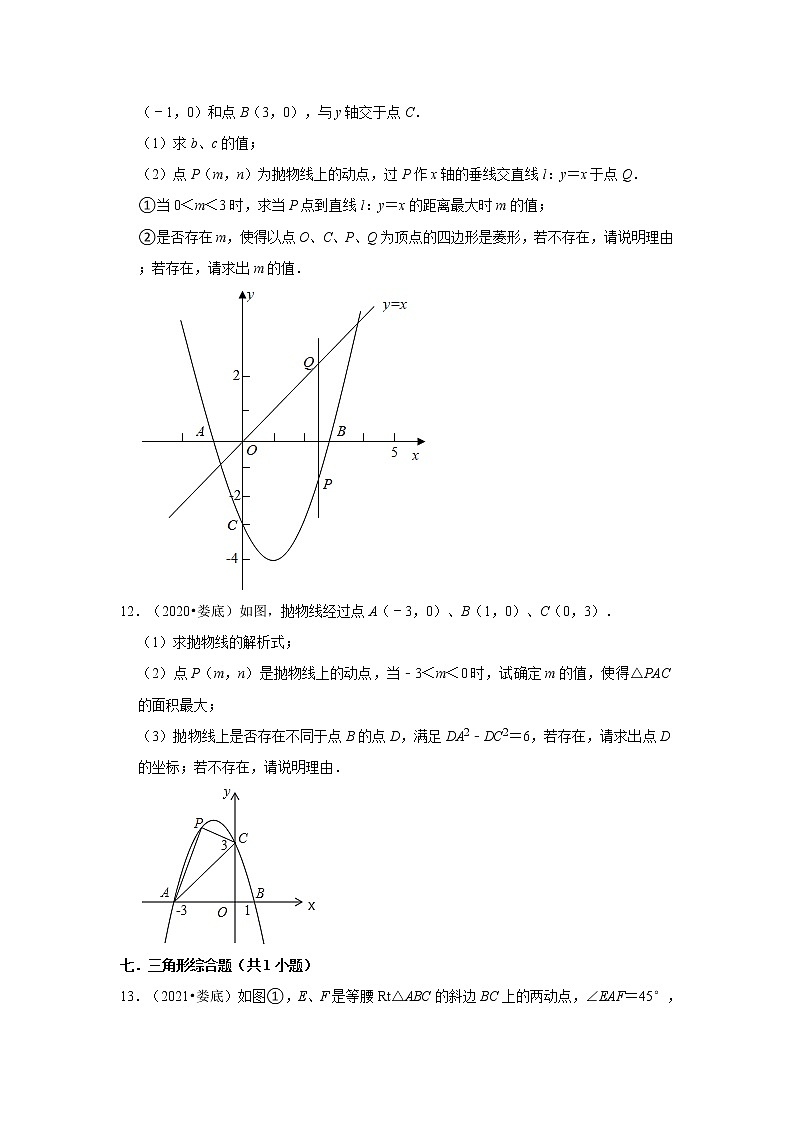
11.(2021•娄底)如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求b、c的值;
(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.
①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;
②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
12.(2020•娄底)如图,抛物线经过点A(﹣3,0)、B(1,0)、C(0,3).
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上的动点,当﹣3<m<0时,试确定m的值,使得△PAC的面积最大;
(3)抛物线上是否存在不同于点B的点D,满足DA2﹣DC2=6,若存在,请求出点D的坐标;若不存在,请说明理由.
七.三角形综合题(共1小题)
13.(2021•娄底)如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:EF2=BE2+CF2;
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设AB=,请利用(2)的结论证明:当α+β=45°时,tan(α+β)=成立.
八.平行四边形的性质(共1小题)
14.(2020•娄底)如图,▱ABCD中,BC=2AB,AB⊥AC,分别在边BC、AD上的点E与点F关于AC对称,连接EF、AE、CF、DE.
(1)试判定四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
九.圆周角定理(共1小题)
15.(2022•娄底)如图,以BC为边分别作菱形BCDE和菱形BCFG(点C,D,F共线),动点A在以BC为直径且处于菱形BCFG内的圆弧上,连接EF交BC于点O.设∠G=θ.
(1)求证:无论θ为何值,EF与BC相互平分;并请直接写出使EF⊥BC成立的θ值.
(2)当θ=90°时,试给出tan∠ABC的值,使得EF垂直平分AC,请说明理由.
一十.直线与圆的位置关系(共1小题)
16.(2022•娄底)如图,已知BD是Rt△ABC的角平分线,点O是斜边AB上的动点,以点O为圆心,OB长为半径的⊙O经过点D,与OA相交于点E.
(1)判定AC与⊙O的位置关系,为什么?
(2)若BC=3,CD=,
①求sin∠DBC、sin∠ABC的值;
②试用sin∠DBC和cos∠DBC表示sin∠ABC,猜测sin2α与sinα、cosα的关系,并用α=30°给予验证.
一十一.切线的判定与性质(共2小题)
17.(2021•娄底)如图,点A在以BC为直径的⊙O上,∠ABC的角平分线与AC相交于点E,与⊙O相交于点D,延长CA至M,连结BM,使得MB=ME,过点A作BM的平行线与CD的延长线交于点N.
(1)求证:BM与⊙O相切;
(2)试给出AC、AD、CN之间的数量关系,并予以证明.
18.(2020•娄底)如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
一十二.解直角三角形的应用(共1小题)
19.(2022•娄底)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3cm,即PQ=3cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧长PB=4cm,弹力大小是100N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到点C处,使弹力大小变为300N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k•Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x﹣x0.
一十三.解直角三角形的应用-仰角俯角问题(共2小题)
20.(2021•娄底)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取=1.732,=1.414)
21.(2020•娄底)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端E点距地面5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡度为1:4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m,≈1.41,≈1.73).
一十四.条形统计图(共3小题)
22.(2022•娄底)按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求,各中小学校积极行动,取得了良好的成绩.某中学随机抽取了部分学生对他们一周的课外阅读时间(A:10h以上,B:8h~10h,C:6h~8h,D:6h以下)进行问卷调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息,解答下列问题:
(1)本次调查的学生共 名;
(2)a= ,b= ;
(3)补全条形统计图.
23.(2021•娄底)“读书,点亮未来”,广泛的课外阅读是同学们搜集和汲取知识的一条重要途径.学校图书馆计划购进一批学生喜欢的图书,为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度,随机抽取了部分学生进行问卷调查(每个学生只选其中一类),将所得数据进行分类统计绘制了不完整的统计图表,请根据图中的信息,解答下列问题:
统计表:
频数
频率
A历史类
50
m
B科普类
90
0.45
C生活类
n
0.20
D其它
20
0.10
合计
(1)本次调查的学生共 人;
(2)m= ,n= ;
(3)补全条形统计图.
24.(2020•娄底)我市开展“温馨家园,创文同行”活动,某初中学校倡议学生利用双休日进社区参加义务劳动,为了了解同学们的劳动情况,学校随机调查了部分同学的劳动时间t(h):A.0≤t≤0.5,B.0.5<t≤1,C.1<t≤1.5,D.t>1.5,将所得数据绘制成了如图不完整的统计图:
(1)本次调查参加义务劳动的学生共 人,a= .
(2)补全条形统计图.
(3)扇形图中“0≤t≤0.5”部分的圆心角是 度.
参考答案与试题解析
一.实数的运算(共2小题)
1.(2022•娄底)计算:(2022﹣π)0+()﹣1+|1﹣|﹣2sin60°.
【解答】解:原式=1+2+﹣1﹣2×
=1+2+﹣1﹣
=2.
2.(2020•娄底)计算:|﹣1|﹣3tan30°+(3.14﹣π)0+()﹣1.
【解答】解:原式=﹣1﹣3×+1+2
=﹣1﹣+1+2
=2.
二.分式的化简求值(共3小题)
3.(2022•娄底)先化简,再求值:(x+2+)÷,其中x是满足条件x≤2的合适的非负整数.
【解答】解:原式=(+)÷
=•
=,
∵x≠0且x﹣2≠0,
∴x≠0且x≠2,
∴x=1,
则原式==﹣1.
4.(2021•娄底)先化简,再求值:•(1﹣),其中x是1、2、3中的一个合适的数.
【解答】解:原式=•
=•
=,
由题意得:x≠1,x≠±3,
当x=2时,原式==.
5.(2020•娄底)先化简(﹣)÷,然后从﹣3,0,1,3中选一个合适的数代入求值.
【解答】解:原式=[﹣]•
=•
=(m﹣3)﹣2(m+3)
=m﹣3﹣2m﹣6
=﹣m﹣9,
当m=﹣3,0,3时,原式没有意义,舍去;
当m=1时,原式=﹣1﹣9=﹣10.
三.分母有理化(共1小题)
6.(2021•娄底)计算:(﹣π)0++()﹣1﹣2cos45°.
【解答】解:原式=1++2﹣2×
=1+﹣1+2﹣
=2.
四.二元一次方程组的应用(共2小题)
7.(2022•娄底)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4mg,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为62mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克?
【解答】解:(1)设一片银杏树叶一年的平均滞尘量为xmg,一片国槐树叶一年的平均滞尘量为ymg,
由题意得:,
解得:,
答:一片银杏树叶一年的平均滞尘量为40mg,一片国槐树叶一年的平均滞尘量为22mg;
(2)50000×40=2000000(mg)=2kg,
答:这三棵银杏树一年的平均滞尘总量约2千克.
8.(2021•娄底)为了庆祝中国共产党建党一百周年,某校举行“礼赞百年,奋斗有我”演讲比赛,准备购买甲、乙两种纪念品奖励在活动中表现优秀的学生.已知购买1个甲种纪念品和2个乙种纪念品共需20元,购买2个甲种纪念品和5个乙种纪念品共需45元.
(1)求购买一个甲种纪念品和一个乙种纪念品各需多少元;
(2)若要购买这两种纪念品共100个,投入资金不少于766元又不多于800元,问有多少种购买方案?并求出所花资金的最小值.
【解答】解:(1)设购买一个甲种纪念品需要x元,购买一个乙种纪念品需要y元,
依题意得:,
解得:.
答:购买一个甲种纪念品需要10元,购买一个乙种纪念品需要5元.
(2)设购买m个甲种纪念品,则购买(100﹣m)个乙种纪念品,
依题意得:,
解得:53≤m≤60,
又∵m为整数,
∴m可以为54,55,56,57,58,59,60,
∴共有7种购买方案.
设购买总费用为w元,则w=10m+5(100﹣m)=5m+500,
∵5>0,
∴w随m的增大而增大,
∴当m=54时,w取得最小值,最小值=5×54+500=770.
答:共有7种购买方案,所花资金的最小值为770元.
五.一元一次不等式的应用(共1小题)
9.(2020•娄底)为了预防新冠肺炎疫情的发生,学校免费为师生提供防疫物品.某校花7200元购进洗手液与84消毒液共400瓶,已知洗手液的价格是25元/瓶,84消毒液的价格是15元/瓶.
求:(1)该校购进洗手液和84消毒液各多少瓶?
(2)若购买洗手液和84消毒液共150瓶,总费用不超过2500元,请问最多能购买洗手液多少瓶?
【解答】解:(1)设该校购进洗手液x瓶,该校购进84消毒液y瓶,
依题意有,
解得.
故该校购进洗手液120瓶,该校购进84消毒液280瓶;
(2)设能购买洗手液a瓶,则能购买84消毒液(150﹣a)瓶,
依题意有25a+15(150﹣a)≤2500,
解得a≤25.
故最多能购买洗手液25瓶.
六.二次函数综合题(共3小题)
10.(2022•娄底)如图,抛物线y=x2﹣2x﹣6与x轴相交于点A、点B,与y轴相交于点C.
(1)请直接写出点A,B,C的坐标;
(2)点P(m,n)(0<m<6)在抛物线上,当m取何值时,△PBC的面积最大?并求出△PBC面积的最大值.
(3)点F是抛物线上的动点,作FE∥AC交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.
【解答】解:(1)当x=0时,y=﹣6,
∴C(0,﹣6),
当y=0时,x2﹣2x﹣6=0,
∴x1=6,x2=﹣2,
∴A(﹣2,0),B(6,0);
(2)方法一:如图1,
连接OP,
设点P(m,﹣2m﹣6),
∴S△POC=xP==3m,
S△BOP=|yP|=+2m+6),
∵S△BOC==18,
∴S△PBC=S四边形PBOC﹣S△BOC
=(S△POC+S△POB)﹣S△BOC
=3m+3(﹣+2m+6)﹣18
=﹣(m﹣3)2+,
∴当m=3时,S△PBC最大=;
方法二:如图2,
作PQ⊥AB于Q,交BC于点D,
∵B(6,0),C(0,﹣6),
∴直线BC的解析式为:y=x﹣6,
∴D(m,m﹣6),
∴PD=(m﹣6)﹣(﹣2m﹣6)=﹣+3m,
∴S△PBC===﹣(m﹣3)2+,
∴当m=3时,S△PBC最大=;
(3)如图3,
当▱ACFE时,AE∥CF,
∵抛物线对称轴为直线:x==2,
∴F1点的坐标:(4,﹣6),
如图4,
当▱ACEF时,
作FG⊥AE于G,
∴FG=OC=6,
当y=6时,x2﹣2x﹣6=6,
∴x1=2+2,x2=2﹣2,
∴F2(2+2,6),F3(2﹣2,6),
综上所述:F(4,﹣6)或(2+2,6)或(2﹣2,6).
11.(2021•娄底)如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.
(1)求b、c的值;
(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.
①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;
②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.
【解答】解:(1)由二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),得:
,
解得:,
∴y=x2﹣2x﹣3,
∴b=﹣2,c=﹣3.
(2)①∵点P(m,n)在抛物线上y=x2﹣2x﹣3,
∴P(m,m2﹣2m﹣3),
∴PQ=m﹣(m2﹣2m﹣3)=﹣m2+3m+3=﹣(m﹣)2+,
∵过P作x轴的垂线交直线l:y=x于点Q,
∴Q(m,m),
设点P到直线y=x的距离为h,
∵直线y=x是一三象限的角平分线,
∴PQ=h,
∴当P点到直线l:y=x的距离最大时,PQ取得最大值,
∴当m=时,PQ有最大值,
∴当P点到直线l:y=x的距离最大时,m的值为.
②∵抛物线与y轴交于点C,
∴x=0时,y=﹣3,
∴C(0,﹣3),
∵OC∥PQ,且以点O、C、P、Q为顶点的四边形是菱形,
∴PQ=OC,
又∵OC=3,PQ=|﹣m2+3m+3|,
∴3=|﹣m2+3m+3|,
解得:m1=0,m2=3,m3=,m4=,
当m1=0时,PQ与OC重合,菱形不成立,舍去;
当m2=3时,P(3,0),Q(3,3),
此时,四边形OCPQ是平行四边形,OQ=,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m3=时,Q(,),
此时,四边形OCQP是平行四边形,OQ=,
∴CQ≠OC,平行四边形OCPQ不是菱形,舍去;
当m4=时,Q(,),
此时,四边形OCQP是平行四边形,OQ=,
∴OQ≠OC,平行四边形OCPQ不是菱形,舍去;
综上所述:不存在m,使得以点O、C、P、Q为顶点的四边形是菱形.
12.(2020•娄底)如图,抛物线经过点A(﹣3,0)、B(1,0)、C(0,3).
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上的动点,当﹣3<m<0时,试确定m的值,使得△PAC的面积最大;
(3)抛物线上是否存在不同于点B的点D,满足DA2﹣DC2=6,若存在,请求出点D的坐标;若不存在,请说明理由.
【解答】解:(1)由题意可以假设抛物线的解析式为y=a(x+3)(x﹣1),
把C(0,3)代入,可得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3.
(2)设直线AC的解析式为y=kx+b,
将A(﹣3,0),C(0,3)代入得到,
解得,
∴直线AC的解析式为y=x+3.
当﹣3<m<0时,点P(m,n)在直线AC的上方,过点P作x轴的垂线交AC于Q.
则P(m,﹣m2﹣2m+3),Q(m,m+3),
∴PQ=﹣m2﹣2m+3﹣(m+3)
=﹣m2﹣3m
=﹣(m+)2+,
∵﹣3<m<0,
∴当m=﹣时,PQ的值最大,
此时S△PAC=•PQ•AO=PQ最大,
∴m=﹣.
(3)由A(﹣3,0),B(1,0),C(0,3),可得AB=4,OB=1,OC=3,
∵BC2=10,∠CAO=45°,
∴BA2﹣BC2=6,
连接BC,过点B作AC的垂线交抛物线于D,交AC于H,连接AD,DC,
则∠AHB=90°,∠DBA=∠CAO=45°,
∴DA2﹣DC2=HA2﹣HC2=AB2﹣BC2=6,
∵∠CAO=∠DBA,
∴点H在AB的垂直平分线上,
即点H在抛物线的对称轴x=﹣1上,
∴点D与点C关于抛物线的对称轴x=﹣1对称,
∵C(0,3),
∴点D的坐标为(﹣2,3).
七.三角形综合题(共1小题)
13.(2021•娄底)如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:EF2=BE2+CF2;
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设AB=,请利用(2)的结论证明:当α+β=45°时,tan(α+β)=成立.
【解答】证明:(1)∵△ABC是等腰直角三角形,
∴AB=AC,
∴∠B=∠ACB=45°,
∵CD⊥BC,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=45°=∠B,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS);
(2)由(1)知,△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,
∵∠BAC=90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°,
∵∠EAF=45°,
∴∠DAF=∠DAE﹣∠EAF=45°=∠EAF,
∵AF=AF,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,DF2=CF2+CD2,
∵CD=BE,
∴EF2=CF2+BE2;
(3)在Rt△ABC中,AC=AB=,
∴BC=AB=2,
∵AH⊥BC,
∴AH=BH=CH=BC=1,
∴BE=1﹣EH,CF=1﹣FH,
由(2)知,EF2=CF2+BE2,
∵EF=EH+FH,
∴(EH+FH)2=(1﹣FH)2+(1﹣EH)2,
∴1﹣EH•FH=EH+FH,
在Rt△AHE中,tanα==EH,
在Rt△AHF中,tanβ==FH,
∴右边====1,
∵α+β=45°,
∴左边=tan(α+β)=tan45°=1,
∴左边=右边,
即当α+β=45°时,tan(α+β)=成立.
八.平行四边形的性质(共1小题)
14.(2020•娄底)如图,▱ABCD中,BC=2AB,AB⊥AC,分别在边BC、AD上的点E与点F关于AC对称,连接EF、AE、CF、DE.
(1)试判定四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
【解答】(1)解:四边形AECF是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE,
∵点E与点F关于AC对称,
∴AE=AF,CE=CF,OE=OF,
在△AOF和△COE中,,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AE=AF=CE=CF,
∴四边形AECF是菱形;
(2)证明:∵BC=2AB,AB⊥AC,
∴∠ACB=30°,
∴∠B=60°,
∵AE=CE,
∴∠EAC=∠ACB=30°,
∴∠BAE=90°﹣30°=60°=∠B,
∴△ABE是等边三角形,
∴AE=AB=BE,∠AEB=60°,
∴∠AEC=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠DCE=180°﹣∠B=120°,
又∵CE=AE,
∴CE=BE=BC=AB=CD,
∴∠CED=∠CDE=30°,
∴∠AED=120°﹣30°=90°,
∴AE⊥DE.
九.圆周角定理(共1小题)
15.(2022•娄底)如图,以BC为边分别作菱形BCDE和菱形BCFG(点C,D,F共线),动点A在以BC为直径且处于菱形BCFG内的圆弧上,连接EF交BC于点O.设∠G=θ.
(1)求证:无论θ为何值,EF与BC相互平分;并请直接写出使EF⊥BC成立的θ值.
(2)当θ=90°时,试给出tan∠ABC的值,使得EF垂直平分AC,请说明理由.
【解答】(1)证明:∵四边形BCFG,四边形BCDE都是菱形,
∴CF∥BG,CD∥BE,CB=CF=CD=BG=BE,
∵D,C,F共线,
∴G,B,E共线,
∴DF∥EG,DF=GE,
∴四边形DEGF是平行四边形,
∴EF与BC互相平分.
当EF⊥FG时,∵GF=BG=BE,
∴EG=2GF,
∴∠GEF=30°,
∴θ=90°﹣30°=60°;
(2)解:当tan∠ABC=2时,EF垂直平分线段AC.
理由:如图(2)中,设AC交EF于点J.
∵四边形BCFG是菱形,
∴∠G=∠FCO=90°,
∵EF与BC互相平分,
∴OC=OB,
∴CF=BC,
∴FC=2OC,
∴tan∠FOC=tan∠ABC,
∴∠ABC=∠FOC,
∴OJ∥AB,
∵OC=OB,
∴CJ=AJ,
∵BC是直径,
∴∠BAC=∠OJC=90°,
∴EF垂直平分线段AC.
一十.直线与圆的位置关系(共1小题)
16.(2022•娄底)如图,已知BD是Rt△ABC的角平分线,点O是斜边AB上的动点,以点O为圆心,OB长为半径的⊙O经过点D,与OA相交于点E.
(1)判定AC与⊙O的位置关系,为什么?
(2)若BC=3,CD=,
①求sin∠DBC、sin∠ABC的值;
②试用sin∠DBC和cos∠DBC表示sin∠ABC,猜测sin2α与sinα、cosα的关系,并用α=30°给予验证.
【解答】解:(1)AC是⊙O切线,理由如下:
如图,连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD是△ABC的角平分线,
∴∠OBD=∠DBC,
∴∠ODB=∠DBC,
∴OD∥BC,
∴∠ODA=∠C=90°,
∵OD是⊙O的半径,且AC⊥OD,
∴AC是⊙O的切线;
(2)①在Rt△DBC中,∵BC=3,CD=,
∴BD===,
∴sin∠DBC===,
如图2,连接DE,OD,过点O作OG⊥BC于G,
∴∠ODC=∠C=∠CGO=90°,
∴四边形ODCG是矩形,
∴OG=CD=,
∵BE是⊙O的直径,
∴∠BDE=90°,
∴cos∠DBE=cos∠CBD,
∴=,
∴=,
∴BE=,
∴OB=BE=,
∴sin∠ABC===;
②∵2sin∠DBC•cos∠DBC=2××=,
∴sin∠ABC=2sin∠DBC•cos∠DBC;
猜想:sin2α=2sinαcosα,理由如下:
当α=30°时,sin2α=sin60°=,
2sinαcosα=2××=,
∴sin2α=2sinαcosα.
一十一.切线的判定与性质(共2小题)
17.(2021•娄底)如图,点A在以BC为直径的⊙O上,∠ABC的角平分线与AC相交于点E,与⊙O相交于点D,延长CA至M,连结BM,使得MB=ME,过点A作BM的平行线与CD的延长线交于点N.
(1)求证:BM与⊙O相切;
(2)试给出AC、AD、CN之间的数量关系,并予以证明.
【解答】证明:(1)∵BC是直径,
∴∠BAC=90°,
∴∠ABE+∠AEB=90°,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵MB=ME,
∴∠MBE=∠MEB,
∴∠MBE+∠EBC=90°,
∴∠MBC=90°,
∴MB⊥BC,
∴BM与⊙O相切;
(2)AC2=CN•AD,
理由如下:∵∠ACD=∠ABD,∠DBC=∠DAC,
∴∠DCA=∠DAC,
∴AD=DC,
∵BC是直径,
∴∠BDC=90°,
∴∠BCD+∠DBC=90°,
∵AN∥BM,BM⊥BC,
∴AN⊥BC,
∴∠N+∠DCB=90°,
∴∠N=∠DBC,
∴∠N=∠DBC=∠DCA=∠DAC,
∴△DAC∽△ANC,
∴,
∴AC2=CN•AD.
18.(2020•娄底)如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
【解答】(1)证明:连接OD,
∵OD=OB,
∴∠ODB=∠OBD,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BE,
∵BE⊥DE,
∴OD⊥DE,
∴DE与⊙O相切;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵BE⊥DE,
∴∠ADB=∠BED=90°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∴△ABD∽△DBE,
∴,
∴=,
∴BD=2;
(3)解:结论CE=AB﹣BE,
理由:过D作DH⊥AB于H,
∵BD平分∠ABC,DE⊥BE,
∴DH=DE,
在Rt△BED与Rt△BHD中,,
∴Rt△BED≌Rt△BHD(HL),
∴BH=BE,
∵∠DCE+∠BCD=∠A+∠BCD=180°,
∴∠DCE=∠A,
∵∠DHA=∠DEC=90°,
∴△ADH≌△CDE(AAS),
∴AH=CE,
∵AB=AH+BH,
∴AB=BE+CE,
∴CE=AB﹣BE.
一十二.解直角三角形的应用(共1小题)
19.(2022•娄底)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3cm,即PQ=3cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧长PB=4cm,弹力大小是100N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到点C处,使弹力大小变为300N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k•Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x﹣x0.
【解答】解:由题意可得,
x0=3cm,
100=k(4﹣3),
解得k=100,
∴F=100Δx,
当F=300时,300=100×(PC﹣3),
解得PC=6cm,
由图可得,
∠PAB=90°,∠PBC=120°,
∴∠APB=30°,
∵PB=4cm,
∴AB=2cm,PA==2(cm),
∵PC=6cm,
∴AC==2(cm),
∴BC=AC﹣AB=(2﹣2)cm,
即BC的长是(2﹣2)cm.
一十三.解直角三角形的应用-仰角俯角问题(共2小题)
20.(2021•娄底)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取=1.732,=1.414)
【解答】解:由题意可得:∠APD=30°,∠BPD=45°,AP=6千米,∠BDP=90°,
在Rt△APD中,∵∠APD=30°,AP=6千米,∠ADP=90°,cos∠APD=cos30°=,
∴AD=AP=3千米,PD=PA•cos30°=6×=3(千米),
在Rt△BPD中,
∵∠BPD=45°,PD=3千米,∠BDP=90°,tan∠BPD=tan45°=,
∴BD=PDtan45°=3(千米),
故AB=BD﹣AD=3﹣3≈5.196﹣3=2.196(千米)=2196米,
则天舟二号从A处到B处的平均速度约为:2196÷7.5≈293(米/秒),
答:天舟二号从A处到B处的平均速度约为293米/秒.
21.(2020•娄底)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端E点距地面5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡度为1:4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m,≈1.41,≈1.73).
【解答】解:作DF⊥AE于F,DG⊥AB于G,CH⊥AB于H,如图所示:
则DF=GA,DC=GH=2,AF=DG=CH,
由题意得:∠EDF=30°,
∴EF=DE=×4=2,DF=EF=2,
∵AE=5,
∴CH=AF=AE﹣EF=5﹣2=3,
∵斜面BC的坡度为1:4=,
∴BH=4CH=12,
∴AB=AG+GH+BH=2+2+12=2+14≈17.5(m),
答:处于同一水平面上引桥底部AB的长约为17.5m.
一十四.条形统计图(共3小题)
22.(2022•娄底)按国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》要求,各中小学校积极行动,取得了良好的成绩.某中学随机抽取了部分学生对他们一周的课外阅读时间(A:10h以上,B:8h~10h,C:6h~8h,D:6h以下)进行问卷调查,将所得数据进行分类,统计绘制了如下不完整的统计图.请根据图中的信息,解答下列问题:
(1)本次调查的学生共 200 名;
(2)a= 30 ,b= 50 ;
(3)补全条形统计图.
【解答】解:(1)本次调查的学生共:10÷5%=200(名),
故答案为:200;
(2)a=×100=30,b=×100=50,
故答案为:30,50;
(3)C类人数为200×15%=30,
补全条形统计图如图:
23.(2021•娄底)“读书,点亮未来”,广泛的课外阅读是同学们搜集和汲取知识的一条重要途径.学校图书馆计划购进一批学生喜欢的图书,为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度,随机抽取了部分学生进行问卷调查(每个学生只选其中一类),将所得数据进行分类统计绘制了不完整的统计图表,请根据图中的信息,解答下列问题:
统计表:
频数
频率
A历史类
50
m
B科普类
90
0.45
C生活类
n
0.20
D其它
20
0.10
合计
(1)本次调查的学生共 200 人;
(2)m= 0.25 ,n= 40 ;
(3)补全条形统计图.
【解答】解:(1)20÷0.10=200(人),
故答案为:200;
(2)m=50÷200=0.25,n=200×0.20=40,
故答案为:0.25,40;
(3)补全条形统计图如下,
24.(2020•娄底)我市开展“温馨家园,创文同行”活动,某初中学校倡议学生利用双休日进社区参加义务劳动,为了了解同学们的劳动情况,学校随机调查了部分同学的劳动时间t(h):A.0≤t≤0.5,B.0.5<t≤1,C.1<t≤1.5,D.t>1.5,将所得数据绘制成了如图不完整的统计图:
(1)本次调查参加义务劳动的学生共 100 人,a= 40 .
(2)补全条形统计图.
(3)扇形图中“0≤t≤0.5”部分的圆心角是 18 度.
【解答】解:(1)本次调查参加义务劳动的学生共35÷35%=100(人),
∵100×a%=40,
∴a=40,
故答案为:100,40;
(2)如图所示:
(3)∵1﹣20%﹣35%﹣×100%=5%,
∴扇形图中“0≤t≤0.5”部分的圆心角是360°×5%=18°,
故答案为:18.
相关试卷
这是一份湖南省岳阳市三年(2020-2022)中考数学真题分类汇编-03解答题,共40页。试卷主要包含了0+|﹣|,+1的值,,B两点等内容,欢迎下载使用。
这是一份湖南省永州市三年(2020-2022)中考数学真题分类汇编-03解答题,共37页。试卷主要包含了﹣1,,其中x=1,其中x=+1,,其中a=2,解关于x的不等式组等内容,欢迎下载使用。
这是一份湖南省邵阳市三年(2020-2022)中考数学真题分类汇编-03解答题,共35页。试卷主要包含了﹣2﹣2sin60°,0﹣|﹣2|﹣tan60°,已知,在抛物线上等内容,欢迎下载使用。








