湖北省齐齐哈尔市三年（2020-2022）中考数学真题分类汇编-02填空题

这是一份湖北省齐齐哈尔市三年（2020-2022）中考数学真题分类汇编-02填空题，共18页。试卷主要包含了如图，直线l，的坐标是 　 　等内容，欢迎下载使用。
湖北省齐齐哈尔市三年（2020-2022）中考数学真题分类汇编-02填空题
一．科学记数法—表示较大的数（共2小题）
1．（2022•齐齐哈尔）据统计，2022届高校毕业生规模预计首次突破千万，约为10760000人，总量和增量均为近年之最，将10760000用科学记数法表示为 　 　．
2．（2020•齐齐哈尔）2020年初新冠肺炎疫情发生以来，近4000000名城乡社区工作者奋战在中国大地的疫情防控一线．将数据4000000用科学记数法表示为　 　．
二．科学记数法—表示较小的数（共1小题）
3．（2021•齐齐哈尔）随着电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.0000007mm2.将0.0000007用科学记数法表示为 　 　．
三．分式方程的解（共2小题）
4．（2022•齐齐哈尔）若关于x的分式方程+＝的解大于1，则m的取值范围是 　 　．
5．（2021•齐齐哈尔）若关于x的分式方程+2的解为正数，则m的取值范围是 　 　．
四．规律型：点的坐标（共3小题）
6．（2022•齐齐哈尔）如图，直线l：y＝x+与x轴相交于点A，与y轴相交于点B，过点B作BC1⊥l交x轴于点C1，过点C1作B1C1⊥x轴交l于点B1，过点B1作B1C2⊥l交x轴于点C2，过点C2作B2C2⊥x轴交l于点B2，⋯，按照如此规律操作下去，则点B2022的纵坐标是 　 　．

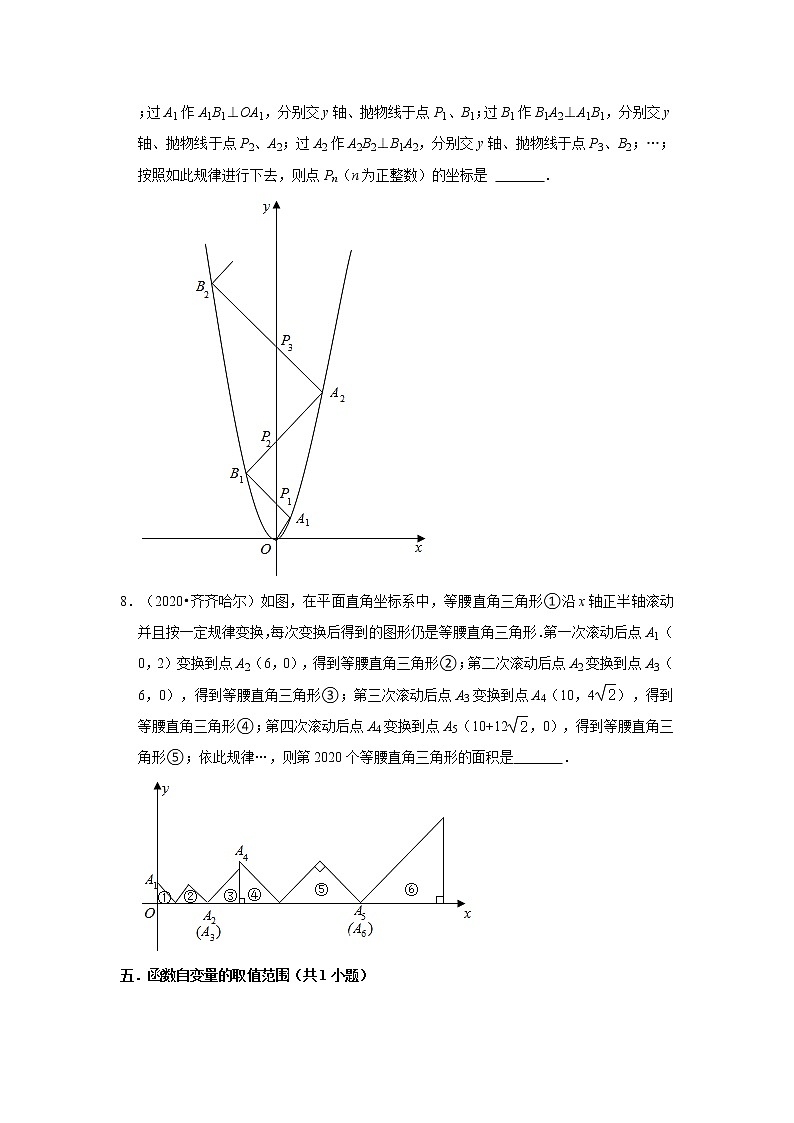
7．（2021•齐齐哈尔）如图，抛物线的解析式为y＝x2，点A1的坐标为（1，1），连接OA1；过A1作A1B1⊥OA1，分别交y轴、抛物线于点P1、B1；过B1作B1A2⊥A1B1，分别交y轴、抛物线于点P2、A2；过A2作A2B2⊥B1A2，分别交y轴、抛物线于点P3、B2；…；按照如此规律进行下去，则点Pn（n为正整数）的坐标是 　 　．

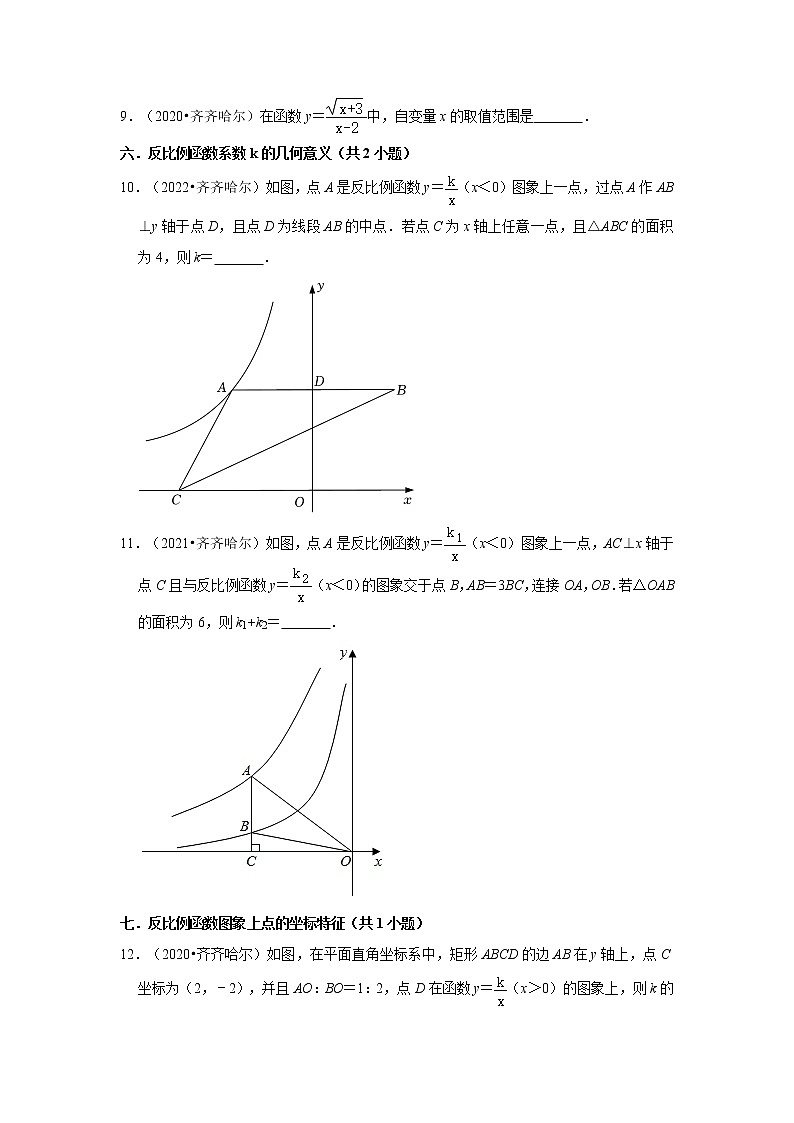
8．（2020•齐齐哈尔）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，4），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+12，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是　 　．

五．函数自变量的取值范围（共1小题）
9．（2020•齐齐哈尔）在函数y＝中，自变量x的取值范围是　 　．
六．反比例函数系数k的几何意义（共2小题）
10．（2022•齐齐哈尔）如图，点A是反比例函数y＝（x＜0）图象上一点，过点A作AB⊥y轴于点D，且点D为线段AB的中点．若点C为x轴上任意一点，且△ABC的面积为4，则k＝　 　．

11．（2021•齐齐哈尔）如图，点A是反比例函数y＝（x＜0）图象上一点，AC⊥x轴于点C且与反比例函数y＝（x＜0）的图象交于点B，AB＝3BC，连接OA，OB．若△OAB的面积为6，则k1+k2＝　 　．

七．反比例函数图象上点的坐标特征（共1小题）
12．（2020•齐齐哈尔）如图，在平面直角坐标系中，矩形ABCD的边AB在y轴上，点C坐标为（2，﹣2），并且AO：BO＝1：2，点D在函数y＝（x＞0）的图象上，则k的值为　 　．

八．全等三角形的判定（共2小题）
13．（2021•齐齐哈尔）如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是 　 　．（只需写出一个条件即可）

14．（2020•齐齐哈尔）如图，已知在△ABD和△ABC中，∠DAB＝∠CAB，点A、B、E在同一条直线上，若使△ABD≌△ABC，则还需添加的一个条件是　 　．（只填一个即可）

九．等腰三角形的性质（共1小题）
15．（2020•齐齐哈尔）等腰三角形的两条边长分别为3和4，则这个等腰三角形的周长是　 　．
一十．勾股定理（共1小题）
16．（2021•齐齐哈尔）直角三角形的两条边长分别为3和4，则这个直角三角形斜边上的高为 　 　．
一十一．菱形的判定（共1小题）
17．（2022•齐齐哈尔）如图，在四边形ABCD中，AC⊥BD，垂足为O，AB∥CD，要使四边形ABCD为菱形，应添加的条件是 　 　．（只需写出一个条件即可）

一十二．圆锥的计算（共2小题）
18．（2022•齐齐哈尔）圆锥的母线长为5cm，高为4cm，则该圆锥侧面展开图扇形的圆心角为 　 　°．
19．（2021•齐齐哈尔）圆锥的底面半径为6cm，它的侧面展开图扇形的圆心角为240°，则该圆锥的母线长为 　 　cm．
一十三．解直角三角形（共1小题）
20．（2022•齐齐哈尔）在△ABC中，AB＝3，AC＝6，∠B＝45°，则BC＝　 　．
一十四．由三视图判断几何体（共1小题）
21．（2020•齐齐哈尔）如图是一个几何体的三视图，依据图中给出的数据，计算出这个几何体的侧面积是　 　．


参考答案与试题解析
一．科学记数法—表示较大的数（共2小题）
1．（2022•齐齐哈尔）据统计，2022届高校毕业生规模预计首次突破千万，约为10760000人，总量和增量均为近年之最，将10760000用科学记数法表示为 　1.076×107　．
【解答】解：10760000＝1.076×107．
故答案为：1.076×107．
2．（2020•齐齐哈尔）2020年初新冠肺炎疫情发生以来，近4000000名城乡社区工作者奋战在中国大地的疫情防控一线．将数据4000000用科学记数法表示为　4×106　．
【解答】解：将数据4000000用科学记数法表示为4×106，
故答案为：4×106．
二．科学记数法—表示较小的数（共1小题）
3．（2021•齐齐哈尔）随着电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.0000007mm2.将0.0000007用科学记数法表示为 　7×10﹣7　．
【解答】解：0.0000007＝7×10﹣7．
故答案为：7×10﹣7．
三．分式方程的解（共2小题）
4．（2022•齐齐哈尔）若关于x的分式方程+＝的解大于1，则m的取值范围是 　m＞0且m≠1　．
【解答】解：，
给分式方程两边同时乘以最简公分母（x+2）（x﹣2），
得（x+2）+2（x﹣2）＝x+2m，
去括号，得x+2+2x﹣4＝x+2m，
解方程，得x＝m+1，
检验：当
m+1≠2，m+1≠﹣2，
即m≠1且m≠﹣3时，x＝m+1是原分式方程的解，
根据题意可得，
m+1＞1，
∴m＞0且m≠1．
故答案为：m＞0且m≠1．
5．（2021•齐齐哈尔）若关于x的分式方程+2的解为正数，则m的取值范围是 　m＜﹣2且m≠﹣3　．
【解答】解：去分母，得：
3x＝﹣m+2（x﹣1），
去括号，移项，合并同类项，得：
x＝﹣m﹣2．
∵关于x的分式方程+2的解为正数，
∴﹣m﹣2＞0．
又∵x﹣1≠0，
∴x≠1．
∴﹣m﹣2≠1．
∴，
解得：m＜﹣2且m≠﹣3．
故答案为：m＜﹣2且m≠﹣3．
四．规律型：点的坐标（共3小题）
6．（2022•齐齐哈尔）如图，直线l：y＝x+与x轴相交于点A，与y轴相交于点B，过点B作BC1⊥l交x轴于点C1，过点C1作B1C1⊥x轴交l于点B1，过点B1作B1C2⊥l交x轴于点C2，过点C2作B2C2⊥x轴交l于点B2，⋯，按照如此规律操作下去，则点B2022的纵坐标是 　（）2022　．

【解答】解：∵y＝x+与x轴相交于点A，与y轴相交于点B，
∴当x＝0时，y＝，当y＝0时，x＝﹣3，
∴A（﹣3，0），B（0，），
∴OA＝3，OB＝，
∴tan∠BAO＝，
∴∠BAO＝30°，
∵BC1⊥l，
∴∠C1BO＝∠BAO＝30°，
∴BC1＝＝2，
∵B1C1⊥x轴，
∴∠B1C1B＝30°，
∴B1C1＝＝，
同理可得，B2C2＝C1＝（）2，
依此规律，可得Bn∁n＝（）n，
当n＝2022时，B2022C2022＝（）2022，
故答案为：（）2022．
7．（2021•齐齐哈尔）如图，抛物线的解析式为y＝x2，点A1的坐标为（1，1），连接OA1；过A1作A1B1⊥OA1，分别交y轴、抛物线于点P1、B1；过B1作B1A2⊥A1B1，分别交y轴、抛物线于点P2、A2；过A2作A2B2⊥B1A2，分别交y轴、抛物线于点P3、B2；…；按照如此规律进行下去，则点Pn（n为正整数）的坐标是 　（0，n2+n）　．

【解答】解：∵点A1（1，1），
∴OA1＝，∠A1OP1＝45°，
∵A1B1⊥OA1，
∴△A1OP1是等腰直角三角形，
∴∠A1P1O＝∠B1P1P2＝45°，OP1＝2，
∴P1（0，2），
∵B1A2⊥A1B1，
∴△B1P1P2是等腰直角三角形，
设P1P2＝2a，则：点B1（﹣a，2+a），
把点B1（﹣a，2+a）代入y＝x2得：a2＝2+a，
解得：a＝2或a＝﹣1（舍），
∴P1P2＝4，
∴P2（0，6），
同理：△A2P3P2是等腰直角三角形，
设P3P2＝2b，则：点A2（b，b+6），
把点A2（b，b+6）代入y＝x2得：b2＝b+6，
解得：b＝3或b＝﹣2（舍），
∴P3P2＝6，
∴P3（0，12），
由P1（0，2），P2（0，6），P3（0，12）可推：
点Pn（0，n2+n）．
故答案为：（0，n2+n）．
8．（2020•齐齐哈尔）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，4），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+12，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是　22020　．

【解答】解：∵点A1（0，2），
∴第1个等腰直角三角形的面积＝＝2，
∵A2（6，0），
∴第2个等腰直角三角形的腰长为＝2，
∴第2个等腰直角三角形的面积＝＝4＝22，
∵A4（10，4），
∴第3个等腰直角三角形的腰长为10﹣6＝4，
∴第3个等腰直角三角形的面积＝＝8＝23，
…
则第2020个等腰直角三角形的面积是22020；
故答案为：22020（形式可以不同，正确即得分）．
五．函数自变量的取值范围（共1小题）
9．（2020•齐齐哈尔）在函数y＝中，自变量x的取值范围是　x≥﹣3且x≠2　．
【解答】解：由题可得，，
解得，
∴自变量x的取值范围是x≥﹣3且x≠2，
故答案为：x≥﹣3且x≠2．
六．反比例函数系数k的几何意义（共2小题）
10．（2022•齐齐哈尔）如图，点A是反比例函数y＝（x＜0）图象上一点，过点A作AB⊥y轴于点D，且点D为线段AB的中点．若点C为x轴上任意一点，且△ABC的面积为4，则k＝　﹣4　．

【解答】解：连接OA，如图所示：

∵AB⊥y轴，
∴AB∥OC，
∵D是AB的中点，
∴S△ABC＝2S△ADO，
∵S△ADO＝，△ABC的面积为4，
∴|k|＝4，
根据图象可知，k＜0，
∴k＝﹣4．
故答案为：﹣4．
11．（2021•齐齐哈尔）如图，点A是反比例函数y＝（x＜0）图象上一点，AC⊥x轴于点C且与反比例函数y＝（x＜0）的图象交于点B，AB＝3BC，连接OA，OB．若△OAB的面积为6，则k1+k2＝　﹣20　．

【解答】解：∵S△AOB＝AB•OC＝6，S△BOC＝BC•OC，AB＝3BC，
∴S△BOC＝2，
∴S△AOC＝2+6＝8，
又∵|k1|＝8，|k2|＝2，k1＜0，k2＜0，
∴k1＝﹣16，k2＝﹣4，
∴k1+k2＝﹣16﹣4＝﹣20，
故答案为：﹣20．
七．反比例函数图象上点的坐标特征（共1小题）
12．（2020•齐齐哈尔）如图，在平面直角坐标系中，矩形ABCD的边AB在y轴上，点C坐标为（2，﹣2），并且AO：BO＝1：2，点D在函数y＝（x＞0）的图象上，则k的值为　2　．

【解答】解：如图，∵点C坐标为（2，﹣2），
∴矩形OBCE的面积＝2×2＝4，
∵AO：BO＝1：2，
∴矩形AOED的面积＝2，
∵点D在函数y＝（x＞0）的图象上，
∴k＝2，
故答案为2．

八．全等三角形的判定（共2小题）
13．（2021•齐齐哈尔）如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是 　∠B＝∠E或∠C＝∠D或AB＝AE　．（只需写出一个条件即可）

【解答】解：∵∠1＝∠2，
∴∠1+∠BAD＝∠2+∠BAD，
即∠BAC＝∠EAD，
∵AC＝AD，
∴当添加∠B＝∠E时，可根据“AAS”判断△ABC≌△AED；
当添加∠C＝∠D时，可根据“ASA”判断△ABC≌△AED；
当添加AB＝AE时，可根据“SAS”判断△ABC≌△AED．
故答案为∠B＝∠E或∠C＝∠D或AB＝AE．
14．（2020•齐齐哈尔）如图，已知在△ABD和△ABC中，∠DAB＝∠CAB，点A、B、E在同一条直线上，若使△ABD≌△ABC，则还需添加的一个条件是　AD＝AC（∠D＝∠C或∠ABD＝∠ABC等）　．（只填一个即可）

【解答】解：∵∠DAB＝∠CAB，AB＝AB，
∴当添加AD＝AC时，可根据“SAS”判断△ABD≌△ABC；
当添加∠D＝∠C时，可根据“AAS”判断△ABD≌△ABC；
当添加∠ABD＝∠ABC时，可根据“ASA”判断△ABD≌△ABC．
故答案为AD＝AC（∠D＝∠C或∠ABD＝∠ABC等）．
九．等腰三角形的性质（共1小题）
15．（2020•齐齐哈尔）等腰三角形的两条边长分别为3和4，则这个等腰三角形的周长是　10或11　．
【解答】解：①3是腰长时，三角形的三边分别为3、3、4，
∵此时能组成三角形，
∴周长＝3+3+4＝10；
②3是底边长时，三角形的三边分别为3、4、4，
此时能组成三角形，
所以周长＝3+4+4＝11．
综上所述，这个等腰三角形的周长是10或11．
故答案为：10或11．
一十．勾股定理（共1小题）
16．（2021•齐齐哈尔）直角三角形的两条边长分别为3和4，则这个直角三角形斜边上的高为 　或　．
【解答】解：设直角三角形斜边上的高为h，
当4是直角边时，斜边长＝＝5，
则×3×4＝×5×h，
解得：h＝，
当4是斜边时，另一条直角边长＝＝，
则×3×＝×4×h，
解得：h＝，
综上所述：直角三角形斜边上的高为或，
故答案为：或．
一十一．菱形的判定（共1小题）
17．（2022•齐齐哈尔）如图，在四边形ABCD中，AC⊥BD，垂足为O，AB∥CD，要使四边形ABCD为菱形，应添加的条件是 　AB＝CD（答案不唯一）　．（只需写出一个条件即可）

【解答】解：添加的条件是AB＝CD，理由如下：
∵AB∥CD，AB＝CD，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形，
故答案为：AB＝CD（答案不唯一）．
一十二．圆锥的计算（共2小题）
18．（2022•齐齐哈尔）圆锥的母线长为5cm，高为4cm，则该圆锥侧面展开图扇形的圆心角为 　216　°．
【解答】解：圆锥的底面圆的半径为：＝3，
设圆锥侧面展开图的圆心角为n°，
则2π×3＝，
∴n＝216，
∴圆锥侧面展开图的圆心角为216°，
故答案为：216．
19．（2021•齐齐哈尔）圆锥的底面半径为6cm，它的侧面展开图扇形的圆心角为240°，则该圆锥的母线长为 　9　cm．
【解答】解：圆锥的底面周长为：2π×6＝12π（cm）；
∴圆锥侧面展开图的弧长为12πcm，
设圆锥的母线长为Rcm，
∴＝12π，
解得R＝9．
故答案为：9．
一十三．解直角三角形（共1小题）
20．（2022•齐齐哈尔）在△ABC中，AB＝3，AC＝6，∠B＝45°，则BC＝　3+3或3﹣3　．
【解答】解：①当△ABC为锐角三角形时，
过点A作AD⊥BC于点D，如图，

∵AB＝3，∠B＝45°，
∴AD＝BD＝AB•sin45°＝3，
∴CD＝＝3，
∴BC＝BD+CD＝3+3；
②当△ABC为钝角三角形时，
过点A作AD⊥BC交BC延长线于点D，如图，

∵AB＝3，∠B＝45°，
∴AD＝BD＝AB•sin45°＝3，
∴CD＝＝3，
∴BC＝BD﹣CD＝3﹣3；
综上，BC的长为3+3或3﹣3．
一十四．由三视图判断几何体（共1小题）
21．（2020•齐齐哈尔）如图是一个几何体的三视图，依据图中给出的数据，计算出这个几何体的侧面积是　65π　．

【解答】解：由三视图可知，原几何体为圆锥，
S侧＝•2πr•l＝×2π×5×13＝65π．
故答案为：65π．