重庆市涪陵区2021-2022学年八年级下学期期末数学试题(word版含答案)

2022年春八年级（下）学业质量监测试卷

数学

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

1．下列二次根式中，是最简二次根式的是（    ）

A．  B．  C．  D．

2．若二次根式在实数范围内有意义，则实数a的取值范围是（    ）

A．  B．  C．  D．

3．在学校春季运动会上，初二年级四个班各派出由16位同学组成的方阵，四个方阵中同学们身高的方差分别是：，，，，则方阵中同学身高最整齐的班级是（    ）

A．1班  B．2班  C．3班  D．4班

4．若一次函数的图象经过第一、二、三象限，则b的取值可以为（    ）

A．  B．  C．0  D．5

5．如图，在□ABCD中，对角线AC，BD相交于点O，已知，，则△的周长为（    ）

A．8  B．9  C．12  D．14 

6．下列四组线段中，不能组成直角三角形的是（    ）

A．，，  B．，，  C．  D．

7．下列不属于菱形性质的是（    ）

A．两组对边分别平行     B．两组对边分别相等 

C．每一条对角线平分一组内角   D．两条对角线相等

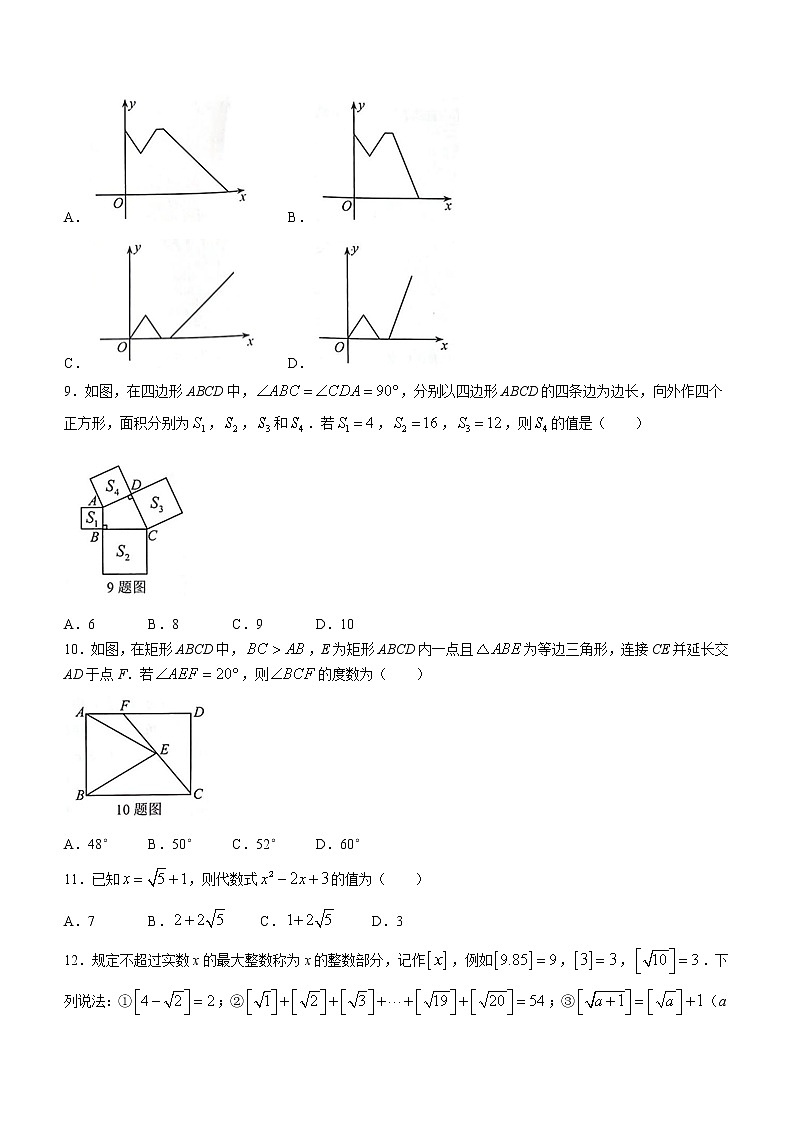
8．小明星期日上午从家步行去重庆市图书馆还书再借书（重庆市图书馆和小明家在同一直线上），小明从家出发匀速走了一会儿后发现自己要还的书没带全，于是以相同的速度匀速折返回家，在家找了一会儿，拿上所有要还的书匀速跑向重庆市图书馆，则小明离家的距离y与时间x之间的函数关系的大致图象是（    ）

A．  B．

C．  D．

9．如图，在四边形ABCD中，，分别以四边形ABCD的四条边为边长，向外作四个正方形，面积分别为，，和．若，，，则的值是（    ）

A．6  B．8  C．9  D．10

10．如图，在矩形ABCD中，，E为矩形ABCD内一点且为等边三角形，连接CE并延长交AD于点F．若，则的度数为（    ）

A．48°  B．50°  C．52°  D．60°

11．已知，则代数式的值为（    ）

A．7  B．  C．  D．3

12．规定不超过实数x的最大整数称为x的整数部分，记作，例如，，．下列说法：①；②；③（a为正整数）；④若n为正整数，且，则n的最小值为6，其中正确说法的个数是（    ）

A．1  B．2  C．3  D．4

二、填空题：（本大题4个小题，每小题4分，共16分）将每小题的答案直接填写在答题卡中对应的横线上．

13．化简______．

14．“清明时节雨纷纷，路上行人欲断魂”，提到清明，很多人会第一时间想起杜牧的这首诗．其实古诗中与清明相关的佳句还有很多，5位同学比赛在相同的时间内背诵与清明相关的古诗，最后的结果为（单位：首）：4，8，9，8，6，则这5位同学在相同的时间内背诵古诗数量的平均数是______首．

15．函数的图象如图所示，点和均在该函数图象上，则______．（用“＞”“＝”或“＜”填空）

16．如图，在正方形ABCD中，，点E，F分别为BC，CD边上的动点，连接AE，BF交于点G，连接DG，点M，N分别为CD，DG的中点，连接MN．若，则MN的最小值为______．

三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

17．计算：（1）；

（2）．

18．如图，在菱形ABCD中，E，F，G分别为AB，BC，CD边上的点，连接AF，CE，AG，若，．求证：

（1）；

（2）四边形AECG为平行四边形．

四、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．

19．在1987年11月，世界卫生组织在日本东京举行的第6届吸烟与健康国际会议上建议把每年的4月7日定为世界无烟日，并从1988年开始执行，但从1989年开始，世界无烟日改为每年的5月31日，因为第二天是国际儿童节，希望下一代免受烟草危害．在第35个世界无烟日即将到来之际，为了进一步提高居民对吸烟危害的认识 ，营造健康、清洁、无烟的社区环境，甲、乙两个社区联合组织了世界无烟日系列宣传活动，并在活动期间对甲、乙两个社区居民随机进行了问卷调查，填写了“吸烟危害健康知识调查问卷” ．现从两个社区收回的问卷中各随机抽取了20份进行整理分析（问卷满分100分，问卷得分用x表示，共分为四个等级：A．，B．，C．，D．，x均为整数），下面给出了部分信息：甲社区抽取的20份居民填写问卷的得分：55，58，62，63，65，67，69，71，73，76，76，76，78，82，85，88，88，92，93，96．乙社区抽取的20份居民填写问卷中得分C等级包含的所有数据为：73，75，77，77，77，78，78．

甲、乙社区抽取的居民填写问卷得分统计表

根据以上信息，解答下列问题：

（1）直接写出上述表中a，b，c的值；

（2）本次调查乙社区收回的问卷共有400份，估计乙社区居民填写问卷的得分为D等级的人数；

（3）根据以上数据，你认为甲、乙社区居民关于吸烟危害健康知识的认识，哪个社区居民了解得更好？请说明理由（写出一条理由即可）．

20．如图，在平面直角坐标系中，直线与x轴、y轴分别交于A，B两点．将直线沿y轴向上平移6个单位长度得到直线l，直线l与x轴、y轴分别交于C，D两点．

（1）求点C的坐标，并在同一平面直角坐标系中直接画出直线l的图象；

（2）连接BC，DA，求四边形ABCD的面积．

21．如图，城心公园的著名景点B在大门A的正北方向 ，游客可以从大门A沿正西方向行至景点C，然后沿笔直的赏花步道到达景点B；也可以从大门A沿正东方向行至景点D，然后沿笔直的临湖步道到达大门A的正北方的景点E，继续沿正北方向行至景点B（点A，B，C，D，E在同一平面内），其中米，米，米，米．

（1）求A，B两点的距离；

（2）为增强游客的浏览体验，提升公园品质，将从大门A修建一条笔直的玻璃廊桥AF与临湖步道DE交汇于点F，且玻璃廊桥AF垂直于临湖步道DE，求玻璃廊桥AF的长．

22．为大力推动学生广泛深入开展阳光体育运动，促进学生身心健康、体魄强健、全面发展，丰富全体师生课余体育生活，某中学准备购买乒乓球拍和羽毛球拍共200副，通过市场调研发现：买1副乒乓球拍和1副羽毛球拍共需160元，买5副乒乓球拍的费用和买3副羽毛球拍的费用相同．

（1）购买每副乒乓球拍和羽毛球拍分别需要多少元？

（2）若学校购买的羽毛球拍不低于80副，求购买乒乓球拍和羽毛球拍共200副的总费用w元与购买的羽毛球拍的数量a之间的函数关系式，并求出总费用至少为多少元．

23．如图，在平面直角坐标系中，一次函数的图象与x轴交于点，与一次函数的图象交于点．

（1）求一次函数的解析式；

（2）结合图象，当时，请直接写出x的取值范围；

（3）C为x轴上点A右侧一个动点，过点C作y轴的平行线，与一次函数的图象交于点D，与一次函数的图象交于点E．当时，求DE的长．

24．一个三位自然数m，若它的个位数字等于百位数字与十位数字之和，则称这个三位自然数m为“和尾数”．将“和尾数”m的个位数字去掉，得到一个两位数，把减去m的个位数字的差记为．例如：213是“和尾数”，∵，∴213是“和尾数”，．

（1）请判断809，527是否是“和尾数”？并说明理由；如果是，请求出对应的的值；

（2）若一个“和尾数”m的百位数字为x，十位数字为y，且能被13整除，求满足条件的所有“和尾数”m．

25．在□ABCD中，对角线，且，E为CD边上一动点，连接BE交AC于点F，M为线段BE上一动点，连接AM．

（1）如图1，若，，M为BF的中点，求AM的长；

（2）如图2，若M在线段BF上，，作交BE于点N，连接AN，求证：；

（3）如图3，若M在线段EF上，将△ABM沿着AM翻折至同一平面内，得到，点B的对应点为点．当，时，请直接写出的值．

2022年春八年级(下)学业质量监测试卷

数学  参考答案

一、选择题：（本大题共12个小题，每小题4分，共48分）

1～6 CABDBC  7～12 DDBBAB

二、填空题：（本大题共4个小题，每小题4分，共16分）

13．  14．   15．   16．

第16题解析：易证≌（）

∴

取中点，连接、、

∵

∴当点在线段上时，取得最小值

∴

∵点、点分别为的中点

∴，即

三、解答题：（本大题2个小题，每小题8分，共16分）

17．（1）解：原式        ……2分

              ……4分

（2）解：原式        ……2分

                 ……3分

                     ……4分

18．证明：（1）∵在菱形中，

∴．     ……1分

在和中，

∵， ……3分

∴≌（）．……4分

（2）∵在菱形中，

∴，．    ……6分

∵，

∴，

即．            ……7分

∵，，

∴四边形为平行四边形． ……8分

四、解答题：（本大题7个小题，每小题10分，共70分）

19．解：（1），，；           ……3分

（2）（人）                ……5分

答：乙社区居民填写问卷的得分为等级的人数约为人．    ……6分

（3）乙社区居民了解得更好，因为乙社区抽取的居民填写问卷得分的平均数

大于甲社区抽取的居民填写问卷得分的平均数，所以乙社区居民了解得

更好．（用中位数、众数等比较均可）           ……10分

20．解：（1）∵将直线沿轴向上平移个单位长度得到直线，

∴直线解析式为．……2分

当时，，

解得．

∴点的坐标为． ……4分

直线的图象如图所示．  ……5分

（2）对直线，

当时，，解得；

当时，．

∴点的坐标为．   ……7分

∵，

∴．           ……8分

∴

．                     ……10分

21．解：（1）由题意，，

∴在中，． ……1分

∵，，

∴（米）． ……3分

答：两点的距离为米．  ……4分

（2）∵，

∴．……5分

∴在中，．

∵，

∴．      ……7分

∵，

∴．

∴ （米）．  ……9分

答：玻璃廊桥的长为米．    ……10分

22．解：（1）设乒乓球拍每副元，羽毛球拍每副元，由题意得：

                  ，            ……2分

解得  ．               ……4分

答：乒乓球拍每副元，羽毛球拍每副元．   ……5分

（2）由题意得：

．……7分

∵，

∴随的增大而增大．

∵，

∴当时，有最小值，． ……9分

答：总费用元与购买的羽毛球拍的数量之间的函数关系式为

，总费用至少为元．                        ……10分

23．解：（1）∵一次函数的图象交于点，

            ∴，即点．      …………1分

∵一次函数的图象经过点，

∴   解得 ．

∴一次函数的表达式为．   …………… 4分

（2）当时，．      …………… 6分

（3）∵轴，

∴．

设，则，，…………… 7分

∵，

∴．

∴．      ……………8分

∴．

∴，．        ……………9分

∴．      ……………10分

24．解：（1）不是“和尾数”

∵，∴不是“和尾数”．         ……1分

是“和尾数”

∵，∴是“和尾数”，．    ……3分

（2）由题意，的个位数字为，            

∴，．   

∴．   ……5分

∵能被整除，

∴能被整除．                 ……6分

∵，，

∴．

∴．                       ……7分

∴，，．

∴所有满足条件的“和尾数”为或或．   ……10分

25．解：（1）∵，，

∴．      ……1分

∵

∴在中，．……2分

∵为的中点，

∴．           ……4分

（2）作交于点，连接．

∵，，

∴，．

∴．

∵，

∴为等腰直角三角形．

∴．

在和中，

∵，

∴≌（）．

       ∴．     ……5分

∵，

∴．

∵

∴

∴为等腰直角三角形．

∴．

∵，

∴．

∴．

在和中，

∵，

∴≌（）．

∴．

∴．        ……8分

（3）．   ……10分

解析：作于点，设

∵，，

∴，，

，，

．

∵，

∴．

∴．