初中数学湘教版八年级上册3.1 平方根完美版课件ppt

这是一份初中数学湘教版八年级上册3.1 平方根完美版课件ppt，文件包含湘教版8上数学第三章311《平方根的概念》课件pptx、湘教版8上数学第三章311《平方根的概念》课件docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

理解掌握平方根的概念，并能求一个数的平方根和算术平方根。
通过复习平方引出求一个数的平方根，并通过实例探究了平方根和算术平方根，让学生在实例中领悟开平方与平方互为逆运算。
正数、0、负数的平方根和算术平方根的情况。
培养学生比较归纳能力，分类分析问题、解决问题的能力，从实践中总结规律及解题技巧的能力。获得相关数学知识和技能，激发学生学习数学的兴趣。
理解掌握平方根的概念，并能熟练求一个数的平方根和算术平方根。
（ ）2=0.36
（ ）2=1.21
（ ）2=0.49
（ ）2=（-4）2
任何数的平方都是非负数！
某家庭在装修儿童房时需铺地垫10.8m2，刚好用去正方形的地垫30块. 你能算出每块地垫的边长是多少吗？
解：每块正方形地垫的面积是 10.8÷30=0.36(m2).
即：边长×边长=0.36.
∵ 0.62=0.36，
∴面积为0.36m2的正方形地垫的边长是0.6m.
每块的面积：10.8÷30=0.36m2
在实际问题中，有时要找一个数，使它的平方等于给定的数.
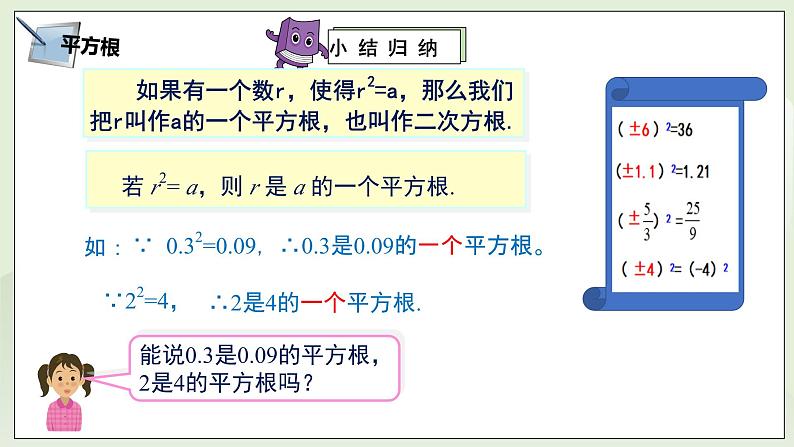
如果有一个数r，使得r2=a，那么我们把r叫作a的一个平方根，也叫作二次方根.
∵ 0.32=0.09，
∴0.3是0.09的一个平方根。
若 r2= a，则 r 是 a 的一个平方根.
能说0.3是0.09的平方根，2是4的平方根吗？
∴2是4的一个平方根.
除了0.3以外，0.09还有其它平方根吗？除以2以外，4还有其它平方根吗？
因为（-0.3）2=0.09，因此-0.3也是0.09的一个平方根；因为(-2)2= 4，因此-2也是4的一个平方根.
如果r是正数a的一个平方根，那么a的平方根有且只有两个：r与-r.
一个正数有两个平方根，它们互为相反数。
∴±0.3是0.09的一个平方根。
∴±2是4的一个平方根.
算术平方根、平方根的表示
由于同号两数相乘得正数，且02=0，即在迄今为止我们所认识的数中，任何一个数的平方都不会是负数，因此负数没有平方根.
一个正数只有一个算术平方根
开平方与平方互为逆运算，根据这种关系，可以求一个数的平方根.
+1-1+2-2+3-3
求一个非负数的平方根的运算，叫作开平方.
因此36的平方根是6与-6.
解：由于1.12=1.21，
因此1.21的平方根是1.1与-1.1.
例2 分别求下列各数的算术平方根： 100， ， 0.49.
解：由于102=100，
解： 由于0.72=0.49，
算术平方根就是正平方根
解： 由于82=64
所以64的平方根是8与-8.
解： 由于2.52=6.25
所以6.25的平方根是2.5与-2.5.
解： 由于92=81
所以81的算术平方根是9
解： 由于0.42=0.16
所以0.16的算术平方根是0.4.
3. 判断下列说法是否正确.
（4）(-4)2的平方根是-4.
(-4)2=16,因此(-4)2的平方根就是16的平方根
若 r2= a，则 r 是 a 的一个平方根.
求一个非负数的平方根的运算.
开平方与平方互为逆运算.
有两个互为相反的平方根.
正数的算术平方根是它的正的平方根.
”0”的算术平方根是0.
负数的没有算术平方根.
课作：P110 习题3.1 第1、2题家作：P111 习题3.1 第3、7题并预习课本第108~110页