



山东省2022年中考数学(五四制)一轮课件:小专题(三) 全等三角形的模型
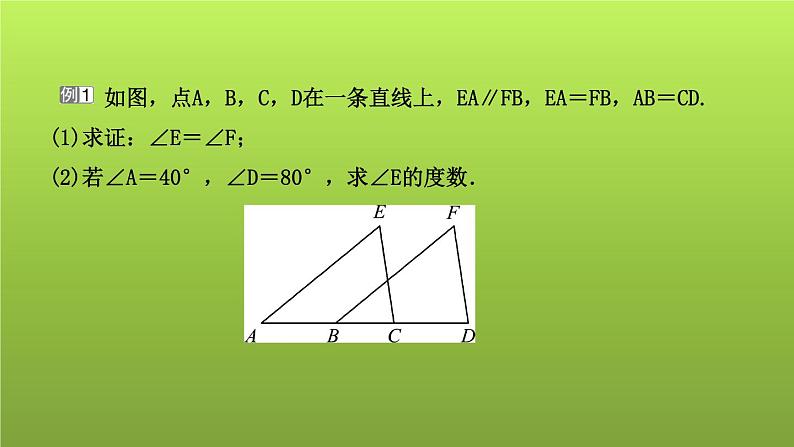
展开【模型分析】 模型特征是有一组边共线或部分重合,另两组边分别平行,常要在移动方向上加(减)公共线段,构造线段相等或利用平行线的性质找到对应角相等.
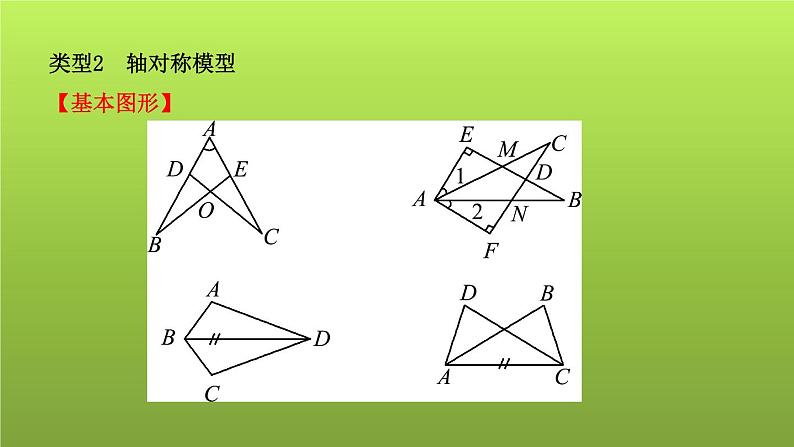
如图,点A,B,C,D在一条直线上,EA∥FB,EA=FB,AB=CD.(1)求证:∠E=∠F;(2)若∠A=40°,∠D=80°,求∠E的度数.
【思路分析】 (1)欲证明∠E=∠F,只要证明△ACE≌△BDF即可;(2)由△EAC≌△FBD 得,∠ACE=∠D=80°,从而可求出∠E的度数.
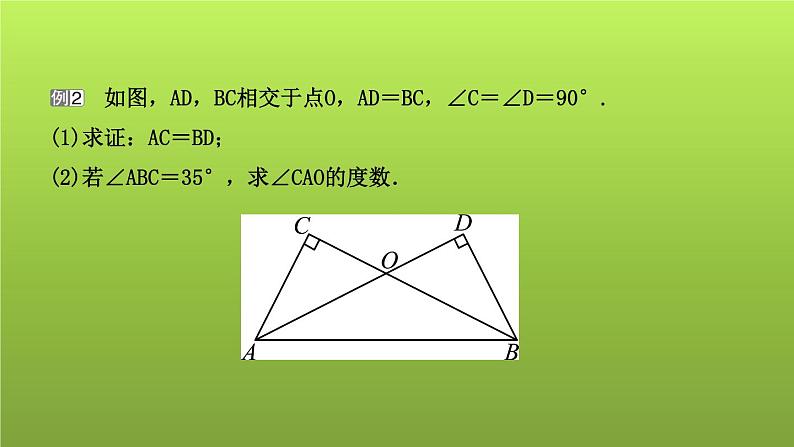
类型2 轴对称模型【基本图形】
【模型分析】 模型特征是所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.(1)求证:AC=BD;(2)若∠ABC=35°,求∠CAO的度数.
【思路分析】 (1)由“HL”可证Rt△ACB≌Rt△BDA,再根据全等三角形的性质即可得解;(2)由全等三角形的性质可得∠BAD=∠ABC=35°,再根据角的和差即可求解.
类型3 半角模型【基本图形】
【模型分析】 1.“半角模型”特征(1)共端点的等线段;(2)共顶点的倍半角;2.“半角模型”主要分为等腰直角三角形内的半角和正方形内的半角.
如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,点M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为 .
【思路分析】 将△ACN绕点A顺时针旋转,得到△ABE,由旋转得出∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,求出∠EAM=∠MAN,根据SAS推出△AEM≌△ANM,根据全等得出MN=ME,求出MN=CN+BM,解直角三角形求出DC的值,即可求出△DMN的周长为BD+DC,代入求出答案即可.
如图,在正方形ABCD中,点E,F分别在BC,AB上,且∠FDE=45°,连接DE,DF,EF,试探究EF,AF,CE之间的数量关系.
【思路分析】 利用旋转将△DAF与△DCE拼接起来,构造全等三角形,借助全等三角形的判定与性质解答即可.
解:EF=AF+CE.
类型4 旋转模型【基本图形】
【模型分析】 模型可看成是将三角形绕着某个点旋转一定角度所构成的,旋转后的图形与原图之间一般存在一对隐含的等角,通过对顶角相等或平行线性质得到或运用角的和差可得到.
如图,△ACD和△ABE均为等腰直角三角形,其中AC=AD=2,AB=AE=2,∠BAE=∠DAC=90°,点B在CD的延长线上,连接CE.(1)求△ABC的面积;(2)求tan∠CBE的值.
【思路分析】 (1)过点A作AF⊥BC于点F,根据勾股定理得出BF的长,进而利用三角形面积公式解答即可;(2)根据等腰直角三角形的性质得出AB=AE,AD=AC,利用SAS证明△BAD和△EAC全等,进而利用全等三角形的性质和三角函数解答即可.
类型5 一线三垂直型【基本图形】【模型分析】 一线:经过直角顶点的直线;三垂直:直角两边互相垂直,作过直角两边的直线互相垂直,利用“同角的余角相等”转化找等角.
如图,四边形ABCD是正方形,E是CD边上任意一点,连接AE,作BF⊥AE,DG⊥AE,垂足分别为F,G.求证:BF-DG=FG.
【思路分析】 根据正方形的性质可得AB=AD,再利用同角的余角相等求出∠BAF=∠ADG,证明△BAF和△ADG全等,根据全等三角形对应边相等可得BF=AG,再利用线段的和与差可得结论.
【规范解答】 证明:∵四边形ABCD是正方形,∴AB=AD,∠DAB=90°.∵BF⊥AE,DG⊥AE,∴∠AFB=∠AGD=∠ADG+∠DAG=90°.
中考数学专题突破---全等三角形中的常考模型 课件: 这是一份中考数学专题突破---全等三角形中的常考模型 课件,共26页。PPT课件主要包含了平移型,轴对称型,旋转型,一线三等角型,目录Contents,有公共边,有公共顶点,不共顶点,共顶点等内容,欢迎下载使用。
2023年中考数学小专题复习课件3 全等三角形的模型: 这是一份2023年中考数学小专题复习课件3 全等三角形的模型,共16页。PPT课件主要包含了规范解答等内容,欢迎下载使用。
初中数学人教版八年级上册12.1 全等三角形习题ppt课件: 这是一份初中数学人教版八年级上册12.1 全等三角形习题ppt课件,共26页。












