


山东省2022年中考数学(五四制)一轮课件:小专题(六) 轴对称——最值问题的方法
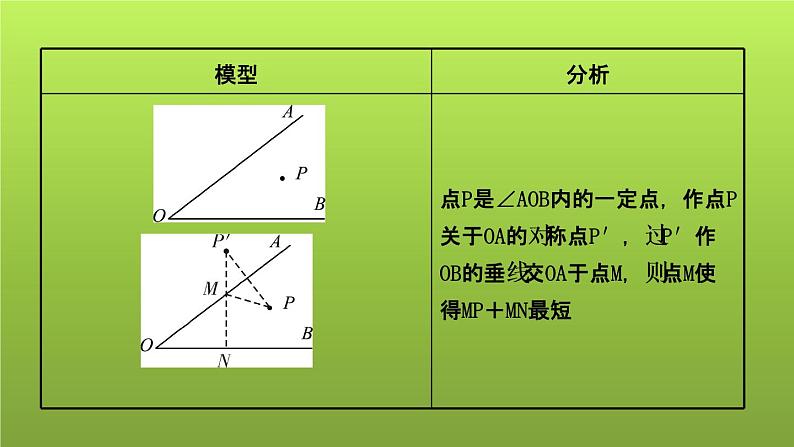
展开如图,点P是∠AOB内的一定点,在射线OA上找一点M,使得点M到点P的距离与到OB的距离之和最短.
【思路分析】 ∵点M在OA上运动,∴点M到点P关于OA的对称点的距离与到点P的距离是相等的,而要求点M到OB的距离,只需过点M作OB的垂线段即可.
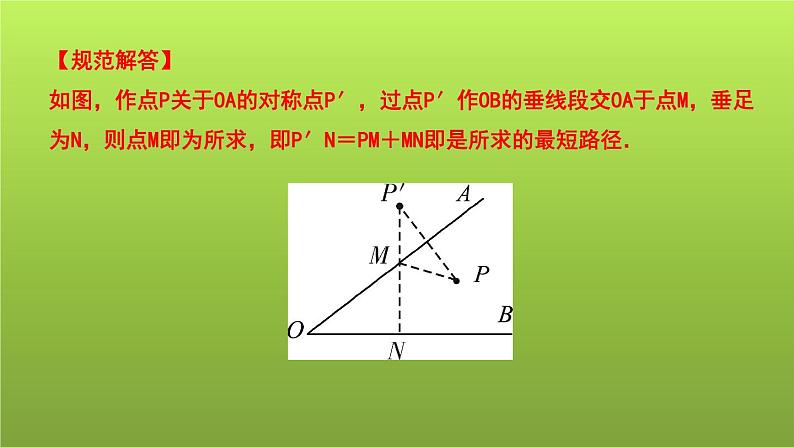
【规范解答】如图,作点P关于OA的对称点P′,过点P′作OB的垂线段交OA于点M,垂足为N,则点M即为所求,即P′N=PM+MN即是所求的最短路径.
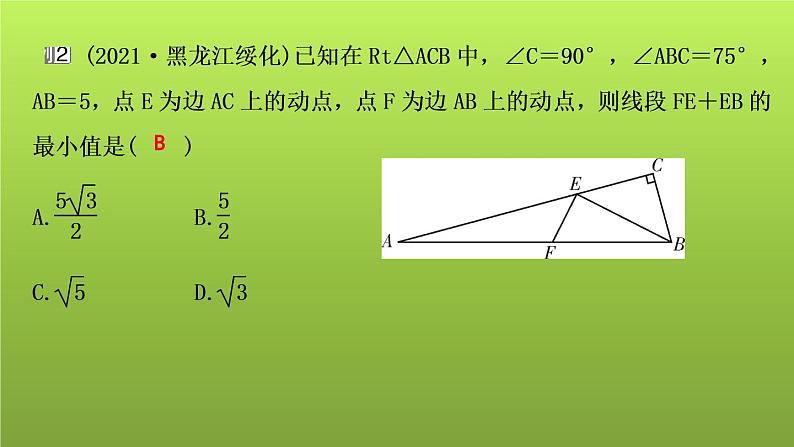
【思路分析】作F关于AC的对称点F′,延长AF′,BC交于点B′,当B,E,F′共线且与AB′垂直时,即求BD的长即可.
如图,已知△ABC为等腰直角三角形,AC=BC=4,∠BCD=15°,点P为CD上的动点,则|PA-PB|的最大值是( )A.4 B.5 C.6 D.8【思路分析】作点A关于CD的对称点A′,连接A′B交CD于点P,则点P就是使|PA-PB|的值最大的点,|PA-PB|=A′B,连接A′C,根据等腰直角三角形的性质得到∠CAB=∠ABC=45°,∠ACB=90°,根据三角形的内角和得到∠ACD=75°,于是得到∠CAA′=15°,根据轴对称的性质得到A′C=BC,∠CA′A=∠CAA′=15°,推出△A′BC是等边三角形,根据等边三角形的性质即可得到结论.
如图,在矩形ABCD中,AB=4,AD=5,连接AC,点O是AC的中点,M是AD上一点,且MD=1,点P是BC上一动点,则PM-PO的最大值为 .
【思路分析】连接MO并延长交BC于点P,则此时,PM-PO的值最大,且PM-PO的最大值为OM,根据全等三角形的性质得到AM=CP=4,OM=OP,求得PB=1,过点M作MN⊥BC于点N,得到四边形MNCD是矩形,得到MN=CD,CN=DM,根据勾股定理即可得到结论.
【思路分析】连接AP,过点A作AH⊥BC于H.说明PA=PC,再根据垂线段最短,解决问题即可.
【思路分析】平移CD使点D落在点B处,连接B′C,则点C的对应点为B′,即B′C=BD,进而得出B′(-3,4),再作点A关于x轴的对称点A′,则A′(0,-2),进而得出AC+BD的最小值为A′B′,即可求解答案.
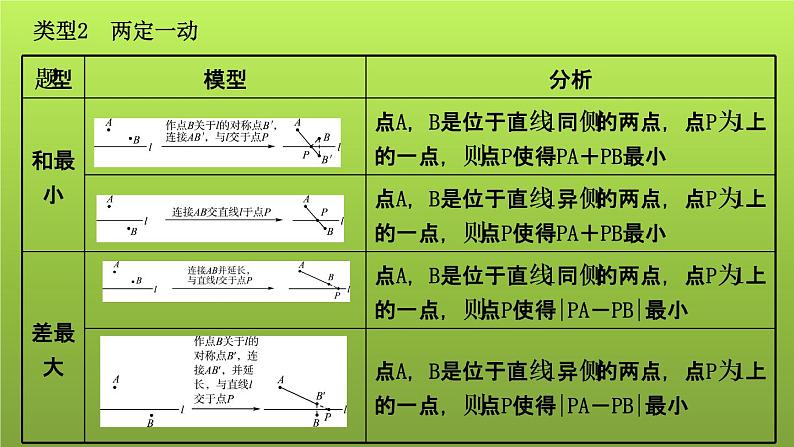
两边及其夹角分别相等的两个三角形全等
三边分别相等的两个三角形全等
中考数学复习微专题七代数最值问题模型一运用配方法求最值课件: 这是一份中考数学复习微专题七代数最值问题模型一运用配方法求最值课件,共6页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
中考数学专题突破---线段最值问题 课件: 这是一份中考数学专题突破---线段最值问题 课件,共26页。PPT课件主要包含了“两定一动“模型,“两动一定“模型,“两定一动”模型,“两动一定”模型等内容,欢迎下载使用。
中考数学专题复习:线段最值问题——“胡不归”(课件): 这是一份中考数学专题复习:线段最值问题——“胡不归”(课件),共13页。PPT课件主要包含了故事引入,学习目标,定理探究,解题步骤,典例精讲,课堂检测,课堂小结等内容,欢迎下载使用。












