广东省深圳中学2021-2022学年七年级下学期期末考试数学试题(word版含答案)

这是一份广东省深圳中学2021-2022学年七年级下学期期末考试数学试题(word版含答案)，共27页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
广东省深圳中学2021-2022学年第二学年七年级期末诊断
数学学科试题
一、选择题（本大题共10小题，共30.0分）
1．（3分）如图所示的四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，其中是轴对称图形的共有（　　）

A．1个 B．2个 C．3个 D．4个
2．（3分）石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m，这个数用科学记数法表示正确的是（　　）
A．3.4×10﹣9 B．0.34×10﹣9 C．3.4×10﹣10 D．3.4×10﹣11
3．（3分）一个三角形的两边长分别是3和7，则第三边长可能是（　　）
A．2 B．9 C．10 D．11
4．（3分）下列运算中，正确的是（　　）
A．x3•x5＝x15
B．2x+3y＝5xy
C．2x2•（3x2﹣5y）＝6x4﹣10x2y
D．（x﹣2）2＝x2﹣4
5．（3分）如图，下列说法中错误的是（　　）

A．∠GBD和∠HCE是同位角 B．∠ABD和∠ACH是同位角
C．∠FBC和∠ACE是内错角 D．∠GBC和∠BCE是同旁内角
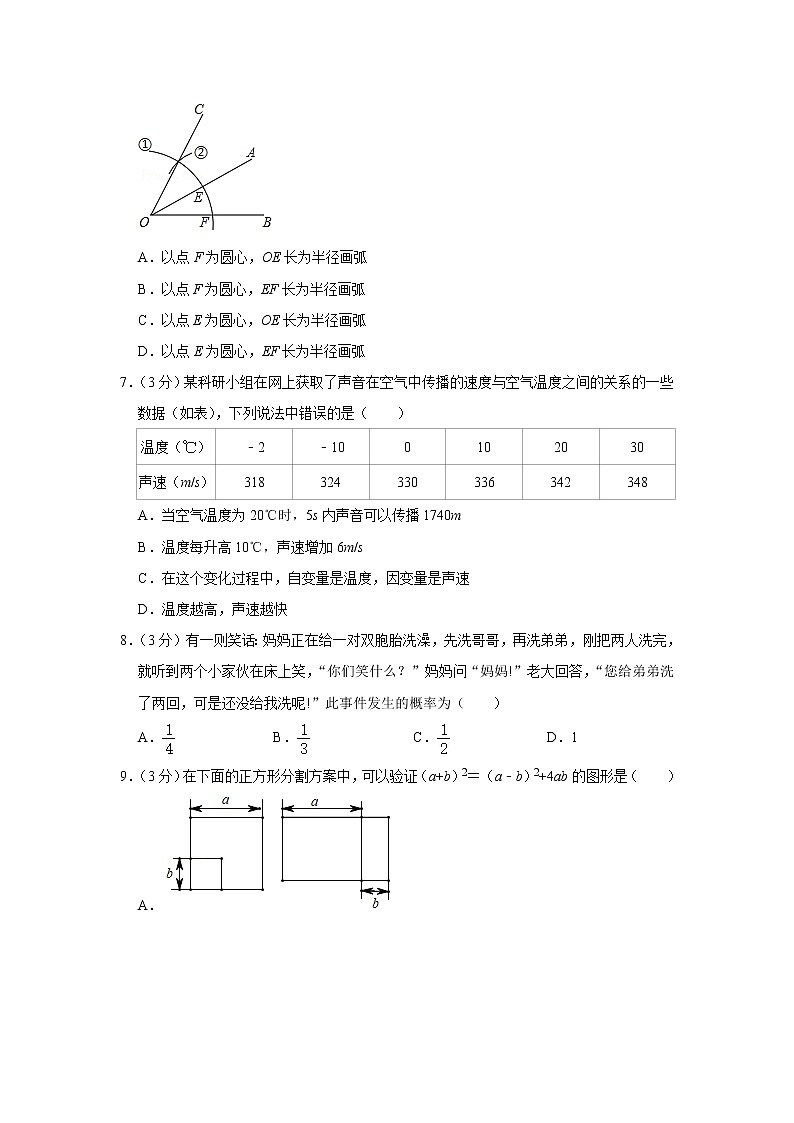
6．（3分）如图，用尺规作图作∠AOC＝∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（　　）

A．以点F为圆心，OE长为半径画弧
B．以点F为圆心，EF长为半径画弧
C．以点E为圆心，OE长为半径画弧
D．以点E为圆心，EF长为半径画弧
7．（3分）某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据（如表），下列说法中错误的是（　　）
温度（℃）
﹣2
﹣10
0
10
20
30
声速（m/s）
318
324
330
336
342
348
A．当空气温度为20℃时，5s内声音可以传播1740m
B．温度每升高10℃，声速增加6m/s
C．在这个变化过程中，自变量是温度，因变量是声速
D．温度越高，声速越快
8．（3分）有一则笑话：妈妈正在给一对双胞胎洗澡，先洗哥哥，再洗弟弟，刚把两人洗完，就听到两个小家伙在床上笑，“你们笑什么？”妈妈问“妈妈!”老大回答，“您给弟弟洗了两回，可是还没给我洗呢!”此事件发生的概率为（　　）
A． B． C． D．1
9．（3分）在下面的正方形分割方案中，可以验证（a+b）2＝（a﹣b）2+4ab的图形是（　　）
A．
B．
C．
D．
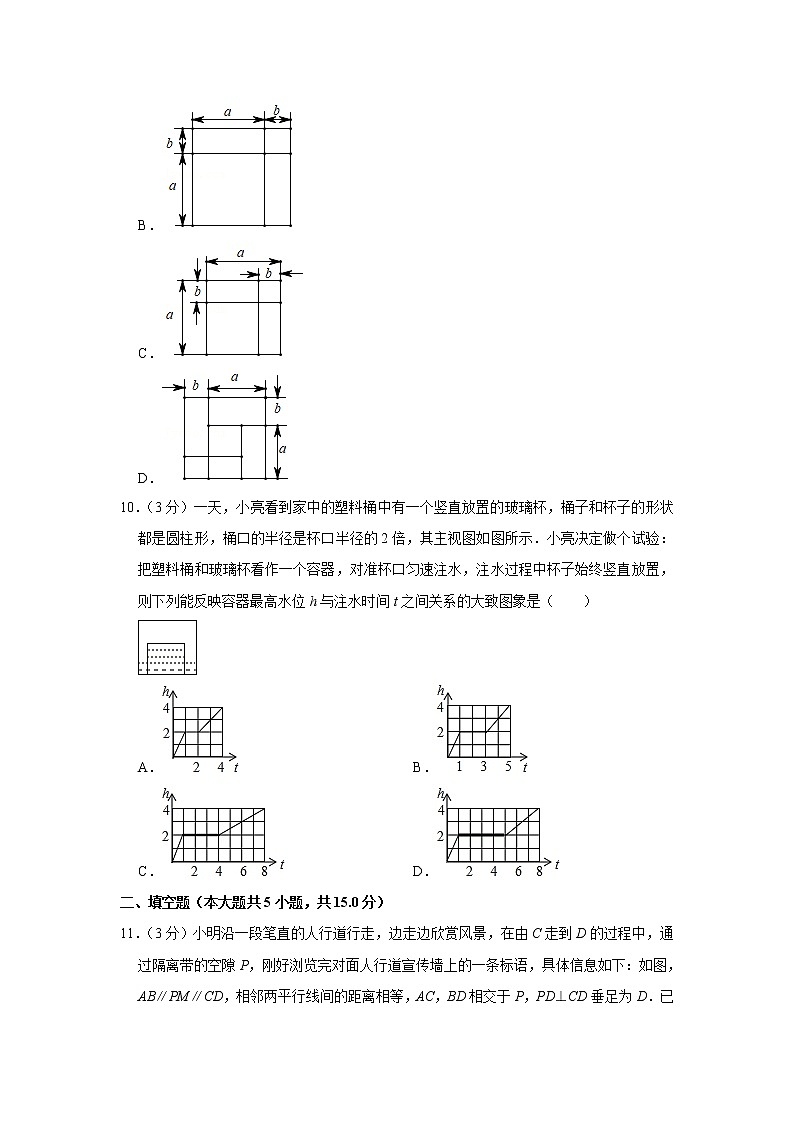
10．（3分）一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶子和杯子的形状都是圆柱形，桶口的半径是杯口半径的2倍，其主视图如图所示．小亮决定做个试验：把塑料桶和玻璃杯看作一个容器，对准杯口匀速注水，注水过程中杯子始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是（　　）

A． B．
C． D．
二、填空题（本大题共5小题，共15.0分）
11．（3分）小明沿一段笔直的人行道行走，边走边欣赏风景，在由C走到D的过程中，通过隔离带的空隙P，刚好浏览完对面人行道宣传墙上的一条标语，具体信息如下：如图，AB∥PM∥CD，相邻两平行线间的距离相等，AC，BD相交于P，PD⊥CD垂足为D．已知CD＝165米．请根据上述信息求标语AB的长度 　 　．

12．（3分）一把直尺与一块三角板如图放置，若∠1＝47°，则∠2的度数为 　 　．

13．（3分）已知m2﹣5m﹣1＝0，则＝　 　．
14．（3分）如图，是一块三角形纸板，其中AD＝DF，BE＝ED，EF＝FC，一只蚂蚁在这张纸上自由爬行，则蚂蚁踩到阴影部分的概率为 　 　．

15．（3分）如图，在△ABC中，∠ACB＝90°，AC＝5，BC＝12，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值等于　 　．

三、计算题（本大题共1小题，第1小题4分，第2小题3分，共7.0分）
16．（7分）计算：
（1）．
（2）x•x5+（﹣2x3）2﹣3x8÷x2．
四、解答题（本大题共6小题，共48.0分）
17．先化简，再求值：[（a﹣2b）2﹣（a﹣2b）（a+2b）+4b2]÷（﹣2b），其中a＝1，b＝﹣2．
18．如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点三角形ABC（三角形的顶点都在网格格点上）．
（1）在图中画出△ABC关于直线l对称的△A′B′C′（要求：点A与点A′、点B与点B′、点C与点C′相对应）；
（2）在（1）的结果下，设AB交直线l于点D，连接AB′，求四边形AB′CD的面积．

19．填空：（将下面的推理过程及依据补充完整）
已知：△ABC的高AD所在直线与高BE所在直线相交于点F，过点F作FG∥BC，交直线AB于点G．如图，若△ABC为锐角三角形，且∠ABC＝45°．
求证：①△BDF≌△ADC；②FG+DC＝AD；
①证明：∵AD，BE为高．
∴∠ADB＝∠BEC＝90°．
∵∠ABC＝45°，
∴∠BAD＝∠　 　＝45°．
∴AD＝　 　．
∵∠BEC＝90°，
∴∠CBE+∠C＝90°（ 　 　）．
又∵∠DAC+∠C＝90°，
∴∠CBE＝∠DAC（ 　 　）．
在△FDB和△CDA中，．
∴△FDB≌△CDA（ 　 　）．
②∵△FDB≌△CDA，
∴DF＝DC（ 　 　）．
∵GF∥BC，
∴∠AGF＝∠ABC＝45°（ 　 　）．
∴∠AGF＝∠　 　．
∴FA＝FG．
∴FG+DC＝FA+DF＝AD．

20．小军与小玲共同发明了一种“字母棋”，进行比胜负的游戏．她们用四种字母做成10只棋子，其中A棋1只，B棋2只，C棋3只，D棋4只．

“字母棋”的游戏规则为：
①游戏时两人各摸一只棋进行比赛称一轮比赛，先摸者摸出的棋不放回；
②A棋胜B棋、C棋；B棋胜C棋、D棋；C棋胜D棋；D棋胜A棋；
③相同棋子不分胜负．
（1）若小玲先摸，问小玲摸到C棋的概率是多少？
（2）已知小玲先摸到了C棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲胜小军的概率是多少？
（3）已知小玲先摸一只棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲希望摸到哪种棋胜小军的概率最大？
21．在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）写出A、B两地之间的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义；
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

22．【初步探索】
（1）如图1：在四边形ABCD中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 　 　；
【灵活运用】
（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；
【拓展延伸】
（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．


广东省深圳中学2021-2022学年第二学年七年级期末诊断
数学学科试题
参考答案与试题解析
一、选择题（本大题共10小题，共30.0分）
1．（3分）如图所示的四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，其中是轴对称图形的共有（　　）

A．1个 B．2个 C．3个 D．4个
【分析】结合轴对称图形的概念求解即可．
【解答】解：①不是轴对称图形，本选项错误；
②不是轴对称图形，本选项错误；
③不是轴对称图形，本选项错误；
④是轴对称图形，本选项正确．
故选：A．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可完全重合．
2．（3分）石墨烯是现在世界上最薄的纳米材料，其理论厚度仅是0.00000000034m，这个数用科学记数法表示正确的是（　　）
A．3.4×10﹣9 B．0.34×10﹣9 C．3.4×10﹣10 D．3.4×10﹣11
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】解：0.00000000034＝3.4×10﹣10，
故选：C．
【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
3．（3分）一个三角形的两边长分别是3和7，则第三边长可能是（　　）
A．2 B．9 C．10 D．11
【分析】根据三角形的三边关系定理：三角形两边之和大于第三边，三角形的两边差小于第三边可得7﹣3＜x＜7+3，再解即可．
【解答】解：设第三边长为x，由题意得：
7﹣3＜x＜7+3，
则4＜x＜10，
所以9适合，
故选：B．
【点评】此题主要考查了三角形的三边关系：第三边的范围是：大于已知的两边的差，而小于两边的和．
4．（3分）下列运算中，正确的是（　　）
A．x3•x5＝x15
B．2x+3y＝5xy
C．2x2•（3x2﹣5y）＝6x4﹣10x2y
D．（x﹣2）2＝x2﹣4
【分析】根据同底数幂的乘法法则，合并同类项，单项式乘多项式的法则，完全平方公式分析选项即可知道答案．
【解答】解：A．x3•x5＝x8，原计算错误，故此选项不符合题意；
B．2x和3y不是同类项，不能合并，原计算错误，故此选项不符合题意；
C．2x2•（3x2﹣5y）＝6x4﹣10x2y，原计算正确，故此选项符合题意；
D．（x﹣2）2＝x2﹣4x+4，原计算错误，故此选项不符合题意；
故选：C．
【点评】本题考查同底数幂的乘法法则，合并同类项，完全平方公式，单项式乘多项式的法则，解题的关键是掌握同底数幂的乘法法则，合并同类项，完全平方公式，单项式乘多项式的法则．
5．（3分）如图，下列说法中错误的是（　　）

A．∠GBD和∠HCE是同位角 B．∠ABD和∠ACH是同位角
C．∠FBC和∠ACE是内错角 D．∠GBC和∠BCE是同旁内角
【分析】根据同位角、同旁内角、内错角的定义结合图形判断．
【解答】解：A、∠GBD和∠HCE不符合同位角的定义，故本选项正确；
B、∠ABD和∠ACH是同位角，故本选项错误；
C、∠FBC和∠ACE是内错角，故本选项错误；
D、∠GBC和∠BCE是同旁内角故本选项错误；
故选：A．
【点评】本题考查了同位角、同旁内角、内错角的定义，属于基础题，正确且熟练掌握同位角、同旁内角、内错角的定义和形状，是解题的关键．
6．（3分）如图，用尺规作图作∠AOC＝∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，那么第二步的作图痕迹②的作法是（　　）

A．以点F为圆心，OE长为半径画弧
B．以点F为圆心，EF长为半径画弧
C．以点E为圆心，OE长为半径画弧
D．以点E为圆心，EF长为半径画弧
【分析】根据作一个角等于已知角的作法即可得出结论．
【解答】解：用尺规作图作∠AOC＝∠AOB的第一步是以点O为圆心，以任意长为半径画弧①，分别交OA、OB于点E、F，
第二步的作图痕迹②的作法是以点E为圆心，EF长为半径画弧．
故选：D．
【点评】本题考查的是作图﹣基本作图，熟知作一个角等于已知角的步骤是解答此题的关键．
7．（3分）某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据（如表），下列说法中错误的是（　　）
温度（℃）
﹣2
﹣10
0
10
20
30
声速（m/s）
318
324
330
336
342
348
A．当空气温度为20℃时，5s内声音可以传播1740m
B．温度每升高10℃，声速增加6m/s
C．在这个变化过程中，自变量是温度，因变量是声速
D．温度越高，声速越快
【分析】根据自变量、因变量的含义，以及声音在空气中传播的速度与空气温度关系逐一判断即可．
【解答】解：A、∵当空气温度为20℃时，声速为342m/s，
∴5s内声音可以传播342×5＝1710（m），
∴选项A错误；
B、∵324﹣318＝6（m/s），330﹣324＝6（m/s），336﹣330＝6（m/s），342﹣336＝6（m/s），348﹣342＝6（m/s），
∴当温度每升高10℃，声速增加6m/s，
∴选项B正确；
C、∵在这个变化中，自变量是温度，因变量是声速，
∴选项C正确；
D、∵根据数据表，可得温度越高，声速越快，
∴选项D正确．
故选：A．
【点评】此题主要考查了自变量、因变量的含义和判断．熟练掌握自变量、因变量的含义是解题的关键．
8．（3分）有一则笑话：妈妈正在给一对双胞胎洗澡，先洗哥哥，再洗弟弟，刚把两人洗完，就听到两个小家伙在床上笑，“你们笑什么？”妈妈问“妈妈!”老大回答，“您给弟弟洗了两回，可是还没给我洗呢!”此事件发生的概率为（　　）
A． B． C． D．1
【分析】根据概率是指某件事发生的可能性为多少解答即可．
【解答】解：此事件发生的概率，
故选：A．
【点评】本题考查了概率的意义，正确理解概率的含义是解决本题的关键．
9．（3分）在下面的正方形分割方案中，可以验证（a+b）2＝（a﹣b）2+4ab的图形是（　　）
A．
B．
C．
D．
【分析】根据图形进行列式表示图形的面积即可．
【解答】解：∵由选项A可得a2﹣b2＝（a+b）（a﹣b），
∴选项A不符合题意；
∵由选项B可得（a+b）2＝a2+2ab+b2，
∴选项B不符合题意；
∵由选项C可得（a﹣b）2＝a2﹣2ab+b2．
∴选项C不符合题意；
∵由选项D可得（a+b）2＝（a﹣b）2+4ab，
∴选项D符合题意；
故选：D．
【点评】此题考查了乘法公式几何意义的几何意义，关键是能根据图形准确列出整式．
10．（3分）一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶子和杯子的形状都是圆柱形，桶口的半径是杯口半径的2倍，其主视图如图所示．小亮决定做个试验：把塑料桶和玻璃杯看作一个容器，对准杯口匀速注水，注水过程中杯子始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是（　　）

A． B．
C． D．
【分析】根据将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内，现用一注水管沿大容器内壁匀速注水，即可求出小水杯内水面的高度h（cm）与注水时间t（min）的函数图象．
【解答】解：一注水管向小玻璃杯内注水，水面在逐渐升高，当小杯中水满时，开始向大桶内流，这时水位高度不变，
因为杯子和桶底面半径比是1：2，则底面积的比为1：4，在高度相同情况下体积比为1：4，杯子内水的体积与杯子外水的体积比是1：3，所以高度不变时，杯外注水时间是杯内注水时间的3倍，当桶水面高度与小杯一样后，再继续注水，水面高度在升高，升高的比开始慢．
故选：C．
【点评】此题主要考查了函数图象，关键是问题的过程，能够通过图象得到函数是随自变量的增大，知道函数值是增大还是减小．
二、填空题（本大题共5小题，共15.0分）
11．（3分）小明沿一段笔直的人行道行走，边走边欣赏风景，在由C走到D的过程中，通过隔离带的空隙P，刚好浏览完对面人行道宣传墙上的一条标语，具体信息如下：如图，AB∥PM∥CD，相邻两平行线间的距离相等，AC，BD相交于P，PD⊥CD垂足为D．已知CD＝165米．请根据上述信息求标语AB的长度 　165米　．

【分析】证明△ABP≌△CDP，即可解决问题．
【解答】解：∵AB∥PM∥CD，PD⊥CD，
∴PB⊥AB，
∴∠ABP＝∠CDP＝90°，
根据题意可知：相邻两平行线间的距离相等，
∴BP＝DP，
在△ABP和△CDP中，
，
∴△ABP≌△CDP（ASA），
∴AB＝CD＝165米．
故答案为：165米．
【点评】本题考查了全等三角形的判定与性质，平行线之间的距离，解决本题的关键是得到△ABP≌△CDP．
12．（3分）一把直尺与一块三角板如图放置，若∠1＝47°，则∠2的度数为 　137°　．

【分析】根据三角形外角定理求出∠3，然后根据两直线平行，同位角相等求解即可．
【解答】解：如图，

∵∠1＝47°，
∴∠3＝∠1+90°＝47°+90°＝137°，
∵直尺的两边互相平行，
∴∠2＝∠3＝137°，
故答案为：137°．
【点评】本题考查了平行线的性质，三角形外角定理，准确识图是解题的关键．
13．（3分）已知m2﹣5m﹣1＝0，则＝　28　．
【分析】由已知条件可以得到m﹣＝5，根据完全平方公式求出m2+的值是27，把所求多项式整理成m2﹣5m+m2+，然后代入数据计算即可．
【解答】解：∵m2﹣5m﹣1＝0，
两边同时除以m得，m﹣＝5，
两边平方，得：
m2﹣2m•+＝25，
∴m2+＝27，
∵2m2﹣5m+＝m2﹣5m+m2+，
＝1+27，
＝28．
故答案为：28．
【点评】本题主要考查完全平方公式，巧妙运用乘积二倍项不含字母点的特点，把多项式整理成已知条件和完全平方式的平方项是解本题的关键，要求同学们在平时的学习中要多动脑，多观察，多总结．
14．（3分）如图，是一块三角形纸板，其中AD＝DF，BE＝ED，EF＝FC，一只蚂蚁在这张纸上自由爬行，则蚂蚁踩到阴影部分的概率为 　　．

【分析】利用等底同高的三角形面积相等的概念，将△ABC分为7个面积相同的三角形，中间阴影部分的三角形的面积是△ABC的，所以蚂蚁踩到阴影部分的概率是．
【解答】解：连接AE，BF，CD，
∵AD＝DF，BE＝ED，EF＝FC，利用三角形中线的性质可得，
∴S△ADC＝S△CDF，S△AED＝S△ABE，S△BEF＝S△EFD，S△EBF＝S△BFC，S△ABD＝S△BDF，S△AEF＝S△AFC，
∴△ABC被分为7个面积相同的三角形，中间阴影部分的三角形的面积是△ABC的，
所以蚂蚁踩到阴影部分的概率是，
故答案为：．

【点评】此题主要考查了三角形中线的性质以及几何概率等知识，利用三角形中线的性质得出面积相等的三角形是解题关键．
15．（3分）如图，在△ABC中，∠ACB＝90°，AC＝5，BC＝12，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值等于　　．

【分析】利用轴对称求最短路径，通过轴对称把问题转化为两点之间线段最短及垂线段最短，再利用三角形相似求解．
【解答】解：
过点C作CG⊥AD于点H，并延长交AB于点G，
则∠AHC＝∠AHG＝90°，
∵AD平分∠CAB，
∴∠CAD＝∠BAD，
∵又AH＝AH，
∴△ACH≌△AGH（ASA），
∴CH＝GH，
∴点C与点G关于AD 对称，
所以CE+EF＝DE+EF，
根据两点之间线段最短及垂线段最短知：
当E，F，G共线且GF⊥AC 时，CE+EF最小，
∵△ACH≌△AGH，
∴AG＝AC＝5，
根据勾股定理得：AB＝13，
∵∠CAB＝∠CAB，∠AFG＝∠ACB＝90°，
∴△AFG≈△ACB，
∴＝，即＝，
解得：FG＝．
故答案为：．
【点评】本题考查了最短路径问题，通过轴对称把问题转化为两点之间线段最短及垂线段最短得转化思想是解题得关键．
三、计算题（本大题共1小题，第1小题4分，第2小题3分，共7.0分）
16．（7分）计算：
（1）．
（2）x•x5+（﹣2x3）2﹣3x8÷x2．
【分析】（1）先化简各式，然后再进行计算即可解答；
（2）先算乘方，再算乘除，后算加减，即可解答．
【解答】解：（1）
＝1+1﹣3+×16
＝1+1﹣3+1
＝0；
（2）x•x5+（﹣2x3）2﹣3x8÷x2
＝x6+4x6﹣3x6
＝2x6．
【点评】本题考查了整式的除法，零指数幂，负整数指数幂，绝对值，同底数幂的乘法，幂的乘方与积的乘方，熟练掌握它们的运算法则是解题的关键．
四、解答题（本大题共6小题，共48.0分）
17．先化简，再求值：[（a﹣2b）2﹣（a﹣2b）（a+2b）+4b2]÷（﹣2b），其中a＝1，b＝﹣2．
【分析】先根据平方差公式和完全平方公式进行计算，再合并同类项，算除法，最后代入求出答案即可．
【解答】解：[（a﹣2b）2﹣（a﹣2b）（a+2b）+4b2]÷（﹣2b）
＝（a2﹣4ab+4b2﹣a2+4b2+4b2）÷（﹣2b）
＝（﹣4ab+12b2）÷（﹣2b）
＝2a﹣6b，
当a＝1，b＝﹣2时，原式＝2×1﹣6×（﹣2）＝2+12＝14．
【点评】本题考查了整式的化简求值，能正确根据整式的运算法则进行化简是解此题的关键，注意运算顺序．
18．如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点三角形ABC（三角形的顶点都在网格格点上）．
（1）在图中画出△ABC关于直线l对称的△A′B′C′（要求：点A与点A′、点B与点B′、点C与点C′相对应）；
（2）在（1）的结果下，设AB交直线l于点D，连接AB′，求四边形AB′CD的面积．

【分析】（1）依据轴对称的性质，即可得到△ABC关于直线l对称的△A′B′C′；
（2）依据割补法进行计算，即可得到四边形AB′CD的面积．
【解答】解：（1）如图所示，△A1B1C1即为所求；

（2）四边形AB′CD的面积为：
4×6﹣×1×1﹣×3×5﹣×1×4＝24﹣0.5﹣7.5﹣2＝14．
【点评】本题主要考查作图﹣轴对称变换，解题的关键是熟练掌握轴对称的定义和性质．
19．填空：（将下面的推理过程及依据补充完整）
已知：△ABC的高AD所在直线与高BE所在直线相交于点F，过点F作FG∥BC，交直线AB于点G．如图，若△ABC为锐角三角形，且∠ABC＝45°．
求证：①△BDF≌△ADC；②FG+DC＝AD；
①证明：∵AD，BE为高．
∴∠ADB＝∠BEC＝90°．
∵∠ABC＝45°，
∴∠BAD＝∠　ABD　＝45°．
∴AD＝　BD　．
∵∠BEC＝90°，
∴∠CBE+∠C＝90°（ 　三角形的内角和定理　）．
又∵∠DAC+∠C＝90°，
∴∠CBE＝∠DAC（ 　同角的余角相等　）．
在△FDB和△CDA中，．
∴△FDB≌△CDA（ 　ASA　）．
②∵△FDB≌△CDA，
∴DF＝DC（ 　全等三角形的对应边相等　）．
∵GF∥BC，
∴∠AGF＝∠ABC＝45°（ 　两直线平行，同位角相等　）．
∴∠AGF＝∠　FAG　．
∴FA＝FG．
∴FG+DC＝FA+DF＝AD．

【分析】①在△ABD中，∠ABC＝45°，AD⊥BC，可证BD＝AD，∠BDF＝∠ADC；在△ADC中，可证得∠AFE＝∠ACD，再根据对顶角相等可得∠ACD＝∠BFD；最后运用AAS，可证明△BDF≌△ADC；
②由△BDF≌△ADC可证得DF＝DC，根据AD＝AF+FD，可得AD＝AF+DC；再由GF∥BD，∠ABC＝45°，可证得AF＝GF，最后得出FG+DC＝AD．
【解答】①证明：∵AD，BE为高．
∴∠ADB＝∠BEC＝90°．
∵∠ABC＝45°，
∴∠BAD＝∠ABD＝45°．
∴AD＝BD．
∵∠BEC＝90°，
∴∠CBE+∠C＝90°（三角形的内角和定理）．
又∵∠DAC+∠C＝90°，
∴∠CBE＝∠DAC（同角的余角相等）．
在△FDB和△CDA中，
．
∴△FDB≌△CDA（ASA）．
②∵△FDB≌△CDA，
∴DF＝DC（全等三角形的对应边相等）．
∵GF∥BC，
∴∠AGF＝∠ABC＝45°（两直线平行，同位角相等）．
∴∠AGF＝∠FAG．
∴FA＝FG．
∴FG+DC＝FA+DF＝AD，
故答案为：ABD，BD，三角形的内角和定理，同角的余角相等，ASA，全等三角形的对应边相等，两直线平行，同位角相等，FAG．

【点评】本题主要考查了三角形全等的判定和性质的运用，解题时注意：利用三角形全等证明线段相等是经常使用的重要方法．
20．小军与小玲共同发明了一种“字母棋”，进行比胜负的游戏．她们用四种字母做成10只棋子，其中A棋1只，B棋2只，C棋3只，D棋4只．

“字母棋”的游戏规则为：
①游戏时两人各摸一只棋进行比赛称一轮比赛，先摸者摸出的棋不放回；
②A棋胜B棋、C棋；B棋胜C棋、D棋；C棋胜D棋；D棋胜A棋；
③相同棋子不分胜负．
（1）若小玲先摸，问小玲摸到C棋的概率是多少？
（2）已知小玲先摸到了C棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲胜小军的概率是多少？
（3）已知小玲先摸一只棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲希望摸到哪种棋胜小军的概率最大？
【分析】本题考查概率问题中的公平性问题，解决本题的关键是计算出各种情况的概率，然后比较即可．概率相等则公平，否则不公平．
【解答】解：（1）小玲摸到C棋的概率等于；
（2）小玲在这一轮中胜小军的概率是．
（3）①若小玲摸到A棋，小玲胜小军的概率是；
②若小玲摸到B棋，小玲胜小军的概率是；
③若小玲摸到C棋，小玲胜小军的概率是；④若小玲摸到D棋，小玲胜小军的概率是．
由此可见，小玲希望摸到B棋，小玲胜小军的概率最大．
【点评】【命题意图】情景简单，背景公平．通过摸棋游戏这个活动考查学生对概率知识的理解，第（3）小题则是需要学生对多种情形进行分析、比较方可得出答案，要求学生有严谨的思维．用到的知识点为：概率＝所求情况数与总情况数之比．
21．在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）写出A、B两地之间的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义；
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

【分析】（1）x＝0时甲的y值即为A、B两地的距离；
（2）根据图象求出甲、乙两人的速度，再利用相遇问题求出相遇时间，然后求出乙的路程即可得到点M的坐标以及实际意义；
（3）分相遇前和相遇后两种情况求出x的值，再求出最后两人都到达B地前两人相距3千米的时间，然后写出两个取值范围即可．
【解答】解：（1）x＝0时，甲距离B地30千米，
所以，A、B两地的距离为30千米；

（2）由图可知，甲的速度：30÷2＝15千米/时，
乙的速度：30÷1＝30千米/时，
30÷（15+30）＝，
×30＝20千米，
所以，点M的坐标为（，20），表示小时后两车相遇，此时距离B地20千米；

（3）设x小时时，甲、乙两人相距3km，
①若是相遇前，则15x+30x＝30﹣3，
解得x＝，
②若是相遇后，则15x+30x＝30+3，
解得x＝，
③若是到达B地前，则15x﹣30（x﹣1）＝3，
解得x＝，
所以，当≤x≤或≤x≤2时，甲、乙两人能够用无线对讲机保持联系．
【点评】本题考查了一次函数的应用，主要利用了路程、速度、时间三者之间的关系，难点在于（3）要分情况讨论．
22．【初步探索】
（1）如图1：在四边形ABCD中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF＝BE+FD，探究图中∠BAE、∠FAD、∠EAF之间的数量关系．
小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 　∠BAE+∠FAD＝∠EAF　；
【灵活运用】
（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；
【拓展延伸】
（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．

【分析】（1）延长FD到点G，使DG＝BE，连接AG，可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF，据此得出结论；
（2）延长FD到点G，使DG＝BE，连接AG，先判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；
（3）在DC延长线上取一点G，使得DG＝BE，连接AG，先判定△ADG≌△ABE，再判定△AEF≌△AGF，得出∠FAE＝∠FAG，最后根据∠FAE+∠FAG+∠GAE＝360°，推导得到2∠FAE+∠DAB＝360°，即可得出结论．
【解答】解：（1）∠BAE+∠FAD＝∠EAF．理由：
如图1，延长FD到点G，使DG＝BE，连接AG，
根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，
再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．
故答案为：∠BAE+∠FAD＝∠EAF；

（2）仍成立，理由：
如图2，延长FD到点G，使DG＝BE，连接AG，
∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，
∴∠B＝∠ADG，
又∵AB＝AD，
∴△ABE≌△ADG（SAS），
∴∠BAE＝∠DAG，AE＝AG，
∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，
∴△AEF≌△AGF（SSS），
∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；

（3）∠EAF＝180°﹣∠DAB．
证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，
∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，
∴∠ADC＝∠ABE，
又∵AB＝AD，
∴△ADG≌△ABE（SAS），
∴AG＝AE，∠DAG＝∠BAE，
∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，
∴△AEF≌△AGF（SSS），
∴∠FAE＝∠FAG，
∵∠FAE+∠FAG+∠GAE＝360°，
∴2∠FAE+（∠GAB+∠BAE）＝360°，
∴2∠FAE+（∠GAB+∠DAG）＝360°，
即2∠FAE+∠DAB＝360°，
∴∠EAF＝180°﹣∠DAB．



【点评】本题属于三角形综合题，主要考查了全等三角形的判定以及全等三角形的性质的综合应用，解决问题的关键是作辅助线构造全等三角形，根据全等三角形的对应角相等进行推导变形．解题时注意：同角的补角相等．