数学必修 第二册8.6 空间直线、平面的垂直教案配套课件ppt

这是一份数学必修 第二册8.6 空间直线、平面的垂直教案配套课件ppt，共25页。PPT课件主要包含了学习目标，新课导入，新课讲解，知识拓展，两条相交直线，线线垂直⇒线面垂直，例题讲解，练习巩固，例题总结，新知讲解等内容，欢迎下载使用。
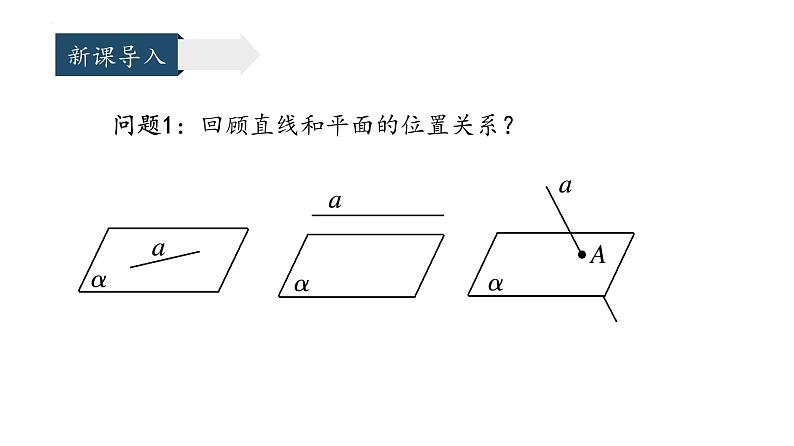
问题1：回顾直线和平面的位置关系？
问题2：在日常生活中，我们对直线与平面垂直有很多感性认识，比如旗杆与地面的位置关系，还有书脊与桌面的垂直关系，给我们以直线与平面垂直的形象，那什么叫做直线与平面垂直呢？
问题3：能否把直观的形象数学化？用确切的数学语言刻画直线与平面垂直
画法：通常把直线画成与表示平面的平行四边形的一边垂直
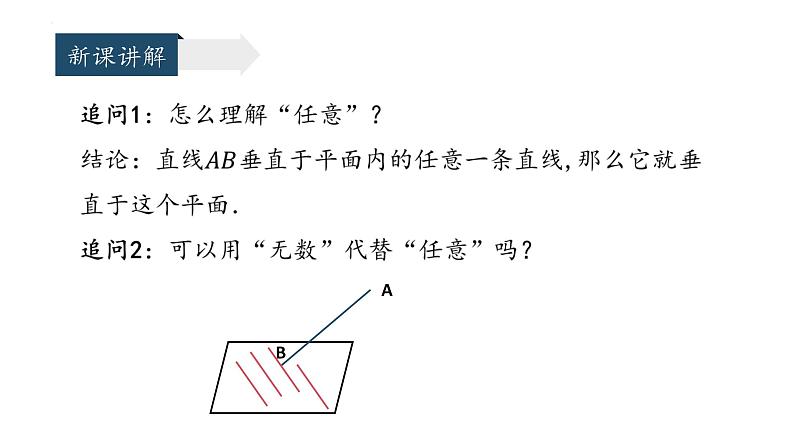
问题4：在同一平面内，过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间，过一点垂直于已知平面的直线有几条?为什么?
过一点有且只有一条直线与已知直线垂直
点到平面距离的定义： 过一点作垂直于已知平面的直线，则该点与垂足间的线段，叫做这个点到该平面的垂线段，垂线段的长度叫做这个点到该平面的距离。
直线与平面垂直的判定定理
问题6：两条相交直线可以确定一个平面,两条平行直线也可以确定一个平面,那么定理中的“两条相交直线”可以改为“两条平行直线”或是“无数条直线”呢?
例1、求证：如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面
证明：(1) 因为SA＝SC，D是AC的中点 所以SD⊥AC.在Rt△ABC中，AD＝BD 由已知SA＝SB 所以△ADS≌△BDS 所以SD⊥BD.又AC∩BD＝D，AC，BD⊂平面ABC 所以SD⊥平面ABC
利用线面垂直的判定定理证明线面垂直的步骤(1)在这个平面内找两条直线，使它们和这条直线垂直(2)确定这个平面内的两条直线是相交的直线(3)根据判定定理得出结论
求斜线与平面所成角的步骤：(1)作图：作(或找)出斜线在平面内的射影，作射影要过斜线上一点作平面的垂线，再过垂足和斜足作直线，注意斜线上点的选取以及垂足的位置要与问题中已知量有关，才能便于计算(2)证明：证明某平面角就是斜线与平面所成的角(3)计算：通常在垂线段、斜线和射影所组成的直角三角形中计算
1、直线与平面垂直的定义2、线面垂直的判定定理3、直线和平面所成的角4、直线与平面垂直的证明与求直线和平面所成的角的方法