湖南省衡阳市2022年中考数学试卷解析版

这是一份湖南省衡阳市2022年中考数学试卷解析版，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

湖南省衡阳市2022年中考数学试卷
一、选择题（本大题共12小题，每小题3分，满分36分，）
1．－2的绝对值是（　　）
A．－2 B．2 C．12 D．−12
【答案】B
【知识点】绝对值及有理数的绝对值
【解析】【解答】解：-2的绝对值是2.
故答案为：B.
【分析】根据负数的绝对值等于它的相反数，可求出其结果.
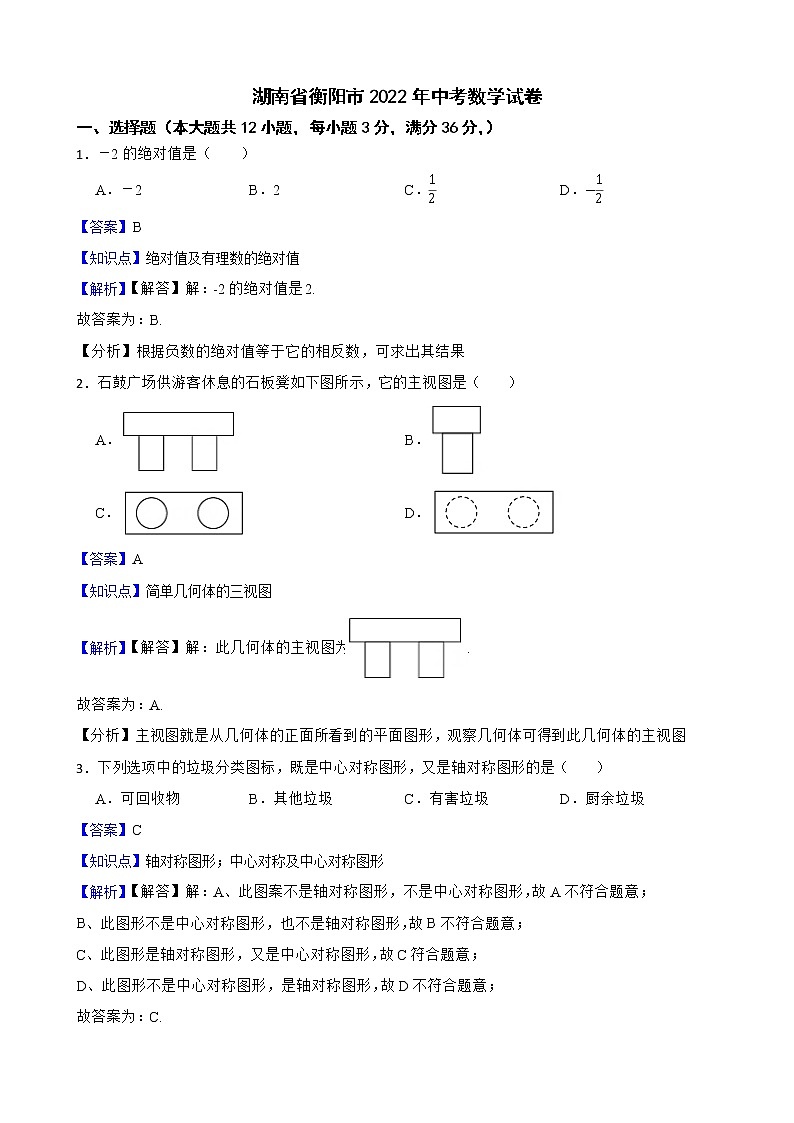
2．石鼓广场供游客休息的石板凳如下图所示，它的主视图是（　　）
A． B．
C． D．
【答案】A
【知识点】简单几何体的三视图
【解析】【解答】解：此几何体的主视图为.
故答案为：A.
【分析】主视图就是从几何体的正面所看到的平面图形，观察几何体可得到此几何体的主视图.
3．下列选项中的垃圾分类图标，既是中心对称图形，又是轴对称图形的是（　　）
A．可回收物 B．其他垃圾 C．有害垃圾 D．厨余垃圾
【答案】C
【知识点】轴对称图形；中心对称及中心对称图形
【解析】【解答】解：A、此图案不是轴对称图形，不是中心对称图形，故A不符合题意；
B、此图形不是中心对称图形，也不是轴对称图形，故B不符合题意；
C、此图形是轴对称图形，又是中心对称图形，故C符合题意；
D、此图形不是中心对称图形，是轴对称图形，故D不符合题意；
故答案为：C.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合，轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合，再对各选项逐一判断.
4．为有效防控新冠疫情，国家大力倡导全国人民免费接种疫苗.截止至2022年5月底，我国疫苗接种高达339000万剂次，数据339000万用科学记数法可表示为a×109的形式，则a的值是（　　）
A．0.339 B．3.39 C．33.9 D．339
【答案】B
【知识点】科学记数法—表示绝对值较大的数
【解析】【解答】解：339000万=3.39×109.
∴a=3.39.
故答案为：B.
【分析】根据科学记数法的表示形式为：a×10n，其中1≤|a|＜10，此题是绝对值较大的数，因此n=整数数位-1.
5．下列运算正确的是（　　）
A．a2+a3=a5 B．a3⋅a4=a12 C．(a3)4=a7 D．a3÷a2=a
【答案】D
【知识点】同底数幂的乘法；同底数幂的除法；合并同类项法则及应用；幂的乘方
【解析】【解答】解：A、a2+a3不能合并，故A不符合题意；
B、a3·a4=a7，故B不符合题意；
C、（a3）4=a12，故C不符合题意；
D、a3÷a2=a，故D符合题意；
故答案为：D.
【分析】只有同类项才能合并，可对A作出判断；利用同底数幂相乘，底数不变，指数相加，可对B作出判断；利用幂的乘方，底数不变，指数相乘，可对C作出判断；利用同底数幂相除，底数不变，指数相减，可对D作出判断.
6．下列说法正确的是（　　）
A．“任意画一个三角形，其内角和为 180DU3 ”是必然事件
B．调查全国中学生的视力情况，适合采用普查的方式
C．抽样调查的样本容量越小，对总体的估计就越准确
D．十字路口的交通信号灯有红、黄、绿三种颜色，所以开车经过十字路口时，恰好遇到黄灯的概率是 13
【答案】A
【知识点】全面调查与抽样调查；事件发生的可能性；简单事件概率的计算
【解析】【解答】解：A、任意画一个三角形，其内角和为180°，是必然事件，故A符合题意；
B、 调查全国中学生的视力情况，适合采用抽样调查的方式 ，故B不符合题意；
C、抽样调查的样本容量越大，对总体的估计就越准确，故C不符合题意；
D、十字路口的交通信号灯有红、黄、绿三种颜色，三种信号灯持续的时间一般不相同，故D不符合题意；
故答案为：A.
【分析】利用三角形的内角和为180°，可对A作出判断；利用抽样调查的定义，可对B作出判断；利用抽样调查的样本容量越大，对总体的估计就越准确，可对C作出判断；根据三种信号灯持续的时间一般不相同，可对D作出判断.
7．如果二次根式 a−1 有意义，那么实数a的取值范围是（　　）
A．a>1 B．a≥1 C．a<1 D．a≤1
【答案】B
【知识点】二次根式有意义的条件
【解析】【解答】解：由题意得
a-1≥0
解之：a≥1.
故答案为：B.
【分析】利用二次根式有意义的条件：被开方数是非负数，可得到关于a的不等式，然后求出不等式的解集.
8．为贯彻落实教育部《关于全面加强新时代大中小学劳动教育的意见》精神，把劳动教育纳入人才培养全过程，某校组织学生周末赴劳动教育实践基地开展锄地、除草、剪枝、捉鱼、采摘五项实践活动，已知五个项目参与人数（单位：人）分别是：35，38，39，42，42，则这组数据的众数和中位数分别是（　　）
A．38，39 B．35，38 C．42，39 D．42，35
【答案】C
【知识点】中位数；众数
【解析】【解答】解：排序为：35，38，39，42，42，
42出现了2次，是出现次数最多的数，
∴这组数据的众数为42；
最中间的数是39，
∴这组数据的中位数是39.
故答案为：C.
【分析】求中位数的方法是：把数据先按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，即可得出答案.
9．不等式组 x+2≥12x A．
B．
C．
D．
【答案】A
【知识点】在数轴上表示不等式组的解集；解一元一次不等式组
【解析】【解答】解： x+2≥1①2x 由①得x≥-1
由②得x＜3
∴不等式组的解集为-1≤x＜3，
故答案为：A.
【分析】分别求出不等式组中的每一个不等式的解集，再确定出不等式组的解集，再观察各选项，可得答案.
10．下列命题为假命题的是（　　）
A．对角线相等的平行四边形是矩形
B．对角线互相垂直的平行四边形是菱形
C．有一个内角是直角的平行四边形是正方形
D．有一组邻边相等的矩形是正方形
【答案】C
【知识点】菱形的判定；矩形的判定；正方形的判定；真命题与假命题
【解析】【解答】解：A、对角线相等的平行四边形是矩形，此命题是真命题，故A不符合题意；
B、对角线互相垂直的平行四边形是菱形，此命题是真命题，故B不符合题意；
C、有一个内角是直角的平行四边形是矩形，原命题是假命题，故C符合题意；
D、有一组邻边相等的矩形是正方形，此命题是真命题，故D不符合题意；
故答案为：C.
【分析】利用矩形的判定定理，可对A作出判断；利用菱形的判定定理，可对B作出判断利用正方形的判定定理，可对C，D作出判断.
11．在设计人体雕像时，使雕像上部（腰部以上）与下部（腰部以下）的高度比，等于下部与全部的高度比，可以增加视觉美感.如图，按此比例设计一座高度为2m 的雷锋雕像，那么该雕像的下部设计高度约是（　　）（结果精确到 0.01m .参考数据： 2≈1.414 ， 3≈1.732 ， 5≈2.236 ）
A．0.73m B．1.24m C．1.37m D．1.42m
【答案】B
【知识点】相似三角形的应用
【解析】【解答】解：设该雕像的下部设计高度约是xm，则上部的高度为（2-x）m，
∵使雕像上部（腰部以上）与下部（腰部以下）的高度比，等于下部与全部的高度比，
∴2-xx=x2
解之：x1=5-1≈1.24，x2=-5-1（舍去）
经检验，x1是方程的根，
故答案为：B.
【解答】设该雕像的下部设计高度约是xm，则上部的高度为（2-x）m，根据雕像上部（腰部以上）与下部（腰部以下）的高度比，等于下部与全部的高度比，建立关于x的方程，解方程求出符合题意的x的值.
12．如图，在四边形 ABCD 中， ∠B=90° ， AC=6 ， AB∥CD ， AC 平分 ∠DAB .设 AB=x ， AD=y ，则 y 关于 x 的函数关系用图象大致可以表示为（　　）
A． B．
C． D．
【答案】D
【知识点】反比例函数的实际应用；等腰三角形的性质；相似三角形的判定与性质
【解析】【解答】∵AB∥CD ，∴∠ACD=∠BAC ，
∵AC 平分 ∠DAB ，∴∠BAC=∠CAD ，
∴∠ACD=∠CAD ，则 CD=AD=y ，即 △ACD 为等腰三角形，
过 D 点做 DE⊥AC 于点 E .
则 DE 垂直平分 AC ， AE=CE=12AC=3 ， ∠AED=90° ，
∵∠BAC=∠CAD ， ∠B=∠AED=90° ，
∴△ABC∽△AED ，
∴ACAD=ABAE ，∴6y=x3 ，
∴y=18x ，
∵在 △ABC 中， AB ∴x<6 ，
故 y 关于 x 的函数图象是D.
故答案为：D.
【分析】利用平行线的性质和角平分线的定义可证得∠ACD=∠CAD，利用等角对等边可证得CD=AD=y，过点D作DE⊥AC于点E，由等腰三角形的性质，可推出DE垂直平分AC，可求出AE的长；再证明是△ABC∽△AED，利用相似三角形的对应边成比例，可得到关于x，y的方程，然后将方程转化为函数解析式，可知此函数是反比例函数且x＜6，观察各选项中的图象，可得到符合题意的选项.
二、填空题（本大题共6个小题，每小题3分，满分18分.）
13．因式分解： x2+2x+1=　 　.
【答案】(x+1)2
【知识点】因式分解﹣运用公式法
【解析】【解答】解： x2+2x+1=(x+1)2 .
故答案为： (x+1)2 .
【分析】利用完全平方公式分解即可.
14．计算：2×8= 　 　.
【答案】4
【知识点】二次根式的乘除法
【解析】【解答】解：原式=2×8=16=4．
故答案为：4
【分析】原式利用二次根式的乘法法则计算，将结果化为最简二次根式即可．
15．计算： 2aa+2+4a+2=　 　.
【答案】2
【知识点】分式的加减法
【解析】【解答】解：原式=2a+4a+2=2a+2a+2=2.
故答案为：2.
【分析】利用同分母分式相加，分母不变，把分子相加，再约分化简.
16．如图，在 △ABC 中，分别以点 A 和点 B 为圆心，大于 12AB 的长为半径作圆弧，两弧相交于点 M 和点 N ，作直线 MN 交 CB 于点 D ，连接 AD .若 AC=8 ， BC=15 ，则 △ACD 的周长为　 　.
【答案】23
【知识点】线段垂直平分线的性质
【解析】【解答】解：由作图可知MN垂直平分AB，
∴AD=BD，
∵△ACD的周长为AC+AD+CD=AC+BD+CD=AC+BC=8+15=23.
故答案为：23.
【分析】利用作图可知MN垂直平分AB，利用线段垂直平分线的性质可证得AD=BD，由此可得到△ACD的周长就是AC+BC，代入计算可求出△ACD的周长.
17．如图，用一个半径为6cm的定滑轮拉动重物上升，滑轮旋转了 120°，假设绳索粗细不计，且与轮滑之间没有滑动，则重物上升了　 　 cm .（结果保留 π）
【答案】4π
【知识点】弧长的计算
【解析】【解答】解：由题意可知物体上升的距离就是半径为6cm，圆心角为120°的弧长，
∴120π×6180=4π
故答案为：4π.
【分析】由题意可知物体上升的距离就是半径为6cm，圆心角为120°的弧长，再利用弧长公式进行计算.
18．回雁峰座落于衡阳雁峰公园，为衡山七十二峰之首.王安石曾赋诗联“万里衡阳雁，寻常到此回”.峰前开辟的雁峰广场中心建有大雁雕塑，为衡阳市城徽.某课外实践小组为测量大雁雕塑的高度，利用测角仪及皮尺测得以下数据：如图， AE=10m ， ∠BDG=30° ， ∠BFG=60° .已知测角仪 DA 的高度为 1.5m ，则大雁雕塑 BC 的高度约为　 　m .（结果精确到 0.1m .参考数据： 3≈1.732 ）
【答案】10.2
【知识点】等腰三角形的性质；解直角三角形的应用
【解析】【解答】∵∠BDG=30° 且 ∠BFG=60° ，
∴∠DBF=∠BFG−∠BDG=30° ，
∴∠DBF=∠BDG ，
即 BF=DF=AE=10m .
∴BG=BF⋅sin60°=53m≈8.66m ，
∴BC=BG+GC=BG+DA=8.66+1.5≈10.2m ，
故答案为 10.2m .
【分析】利用已知条件可证得∠DBF=∠BDG，利用等角对等边可证得BF=DF，可求出BF的长；再利用解直角三角形求出BG的长；然后根据BC=BG+CG，可求出BC的长.
三、解答题（本大题共8个小题，19~20题每题6分，21~24题每题8分，25题10分，26题12分，满分66分..）
19．先化简，再求值. (a+b)(a−b)+b(2a+b) ，其中 a=1 ， b=−2 .
【答案】解：原式 =a2−b2+2ab+b2=a2+2ab ，
将 a=1 ， b=−2 代入式中得：
原式 =12+2×1×(−2)=1−4=−3
【知识点】利用整式的混合运算化简求值
【解析】【分析】利用平方差公式和单项式乘以多项式的法则，先去括号，再合并同类项；然后将a，b的值代入化简后的代数式求值即可.
20．如图，在 △ABC 中， AB=AC ， D 、 E 是 BC 边上的点，且 BD=CE ，求证： AD=AE .
【答案】证明：∵AB=AC ，
∴△ABC 为等腰三角形，
∴∠B=∠C ，
又∵BD=CE ，
∴在 △ABD 和 △ACE 中， AB=AC∠B=∠CBD=CE ，
∴△ABD≌△ACE(SAS) ，
∴AD=AE .
【知识点】等腰三角形的性质；三角形全等的判定（SAS）
【解析】【分析】利用等边对等角可证得∠B=∠C，再利用SAS证明△AD≌△ACE，利用全等三角形的对应边相等，可证得结论.
21．为落实“双减提质”，进一步深化“数学提升工程”，提升学生数学核心素养，某学校拟开展“双减”背景下的初中数学活动型作业成果展示现场会，为了解学生最喜爱的项目，现随机抽取若干名学生进行调查，并将调查结果绘制成如下两幅不完整的统计图：
根据以上信息，解答下列问题：
（1）参与此次抽样调查的学生人数是▲ 人，补全统计图①（要求在条形图上方注明人数）；
（2）图②中扇形 C 的圆心角度数为　 　度；
（3）若参加成果展示活动的学生共有1200人，估计其中最喜爱“测量”项目的学生人数是多少；
（4）计划在 A ， B ， C ， D ， E 五项活动中随机选取两项作为直播项目，请用列表或画树状图的方法，求恰好选中 B ， E 这两项活动的概率.
【答案】（1）解：18；补全统计图如下：
（2）90
（3）解：最喜爱“测量”项目的学生人数是： 30120×1200=300 人
（4）解：列表如下：

A
B
C
D
E
A
——
AB
AC
AD
AE
B
BA
——
BC
BD
BE
C
CA
CB
——
CD
CE
D
DA
DB
DC
——
DE
E
EA
EB
EC
ED
——
或者树状图如下：
所以，选中 B 、 E 这两项活动的概率为： P(选中BE)=220×100%=10% .
【知识点】用样本估计总体；扇形统计图；条形统计图；列表法与树状图法
【解析】【解答】解：（1）因为参与 B 活动的人数为36人，占总人数 30% ，所以总人数 =3630%=120 人，
则参与 E 活动的人数为： 120−30−36−30−6=18 人；
（2）扇形 C 的圆心角为： 30120×360°=90° ；
【分析】（1）参与此次抽样调查的学生人数=B组的人数÷B组的人数所占的百分比，列式计算可求出结果；再求出E组的人数；然后补全条形统计图.
（2）扇形C的圆心角的度数=360°×C的人数所占的百分比，列式计算.
（3）用1200×最喜爱“测量”项目的学生人数所占的百分比，列式计算即可.
（4）由题意可知此事件是抽取不放回，列表，可得到所有等可能的结果数及恰好选中B，E 这两项活动的情况数，然后利用概率公式进行计算.
22．冰墩墩（Bing Dwen Dwen）、雪容融（Shuey Rhon Rhon）分别是2022年北京冬奥会、冬残奥会的吉样物.冬奥会来临之际，冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶，决定从该网店进货并销售，第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个，已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元，销售时每个冰墩墩玩偶可获利28元，每个雪容融玩偶可获利20元.
（1）求两种玩偶的进货价分别是多少？
（2）第二次小雅进货时，网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个，应如何设计进货方案才能获得最大利润，最大利润是多少元？
【答案】（1）解：设冰墩墩进价为 x 元，雪容融进价为 y 元.
得 x+y=13615x+5y=1400 ，解得 x=72y=64 ，
∴冰墩墩进价为72元，雪容融进价为64元.
（2）解：设冰墩墩进货 a 个，雪容融进货 (40−a) 个，设利润为 w ，
得关于利润解析式 w=28a+20(40−a)=8a+800 ，
∵a>0 ，所以利润随 a 增大而增大，
又因为冰墩墩进货量不能超过雪容融进货量的1.5倍，
得 a≤32(40−a) ，解得 a≤24 .
∴当 a 取24时利润取得最大值为992.
【知识点】一次函数的实际应用；二元一次方程组的实际应用-销售问题
【解析】【分析】（1）抓住关键已知条件：第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个，已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元，这里包含两个等量关系；再设未知数，列方程组，然后求出方程组的解.
（2）利用总利润=每一个冰墩墩的利润×其数量+每一个雪容融的利润×其数量，可得到W与a之间的函数解析式，再利用二次函数的性质及a的取值范围，可得到进货方案及最大利润.
23．如图，反比例函数 y=mx 的图象与一次函数 y=kx+b 的图象相交于 A(3，1) ， B(−1，n) 两点.
（1）求反比例函数和一次函数的关系式；
（2）设直线 AB 交 y 轴于点 C ，点 M ， N 分别在反比例函数和一次函数图象上，若四边形 OCNM 是平行四边形，求点 M 的坐标.
【答案】（1）解：∵点A在反比例函数图象上，
∴m=1×3=3，
∴反比例函数解析式为y=3x；
∵点B在反比例函数图象上，
∴-n=3
解之：n=3
∴点B（-1，3），
∵点A，B在一次函数图象上，
∴3k+b=1-k+b=3
解之：k=1b=-2
∴一次函数解析式为y=x-2.
（2）解：由题 OC=2 ，且四边形 OCNM 为平行四边形，且 OC 固定，
∴M ， N 横坐标相同，设 M(t，3t) ， N(t，t−2) ，
∵OC=MN 即 3t−(t−2)=2 ，解得 t=±3 ，
∴M(3，3) 或 (−3，−3)
【知识点】待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题；平行四边形的判定
【解析】【分析】（1）将点A的坐标代入反比例函数解析式，可求出m的值，可得到反比例函数解析式；再将点B的坐标代入反比例函数解析式，可求出n的值，可得到点B的坐标；然后将点A，B的坐标代入一次函数解析式，可得到关于k，b的方程组，解方程组求出k，b的值，由此可得到一次函数解析式.
（2）由题意可知OC=2，再利用平行四边形的性质，可知点M，N的横坐标相同，因此设 M(t，3t) ， N(t，t−2) ，由OC=MN，可得到关于t的方程，解方程求出t的值，即可得到点M的坐标.
24．如图， AB 为 ⊙O 的直径，过圆上一点 D 作 ⊙O 的切线 CD 交 BA 的延长线与点 C ，过点 O 作 OE∥AD 交 CD 于点 E ，连接 BE .
（1）直线 BE 与 ⊙O 相切吗？并说明理由；
（2）若 CA=2 ， CD=4 ，求 DE 的长.
【答案】（1）解：证明：连接 OD .
∵CD 为 ⊙O 切线，∴∠ODC=∠ODE=90° ，
又∵OE∥AD ，∴∠DAO=∠EOB ， ∠ADO=∠EOD ，
且 ∠ADO=∠DAO ，∴∠EOD=∠EOB ，
在 △ODE 与 △OBE 中；
∵OD=OB∠EOD=∠EOBOE=OE ，
∴△ODE≌△OBE ，
∴∠OBE=∠ODE=90° ，
∴直线 BE 与 ⊙O 相切.
（2）解：设半径为 r ；
则： r2+42=(2+r)2 ，得 r=3 ；
在直角三角形 CBE 中， BC2+BE2=CE2 ，
(2+3+3)2+DE2=(4+DE)2 ，解得 DE=6 .
【知识点】勾股定理；切线的判定与性质；三角形全等的判定（SAS）
【解析】【分析】（1）连接OD，利用切线的性质可证得∠ODC=∠ODE=90°，可得到OE∥AD，利用平行线的性质及等边对等角可证得∠DAO=∠EOB，∠ADO=∠EOD，∠ADO=∠DAO，可推出∠EOD=∠EOB；再利用SAS证明△ODE≌△OBE，利用全等三角形的性质可得到∠OBE=90°，然后利用切线的判定定理可证得结论.
（2）设圆的半径为r，利用勾股定理建立关于r的方程，解方程求出r的值；在Rt△CBE中，利用勾股定理可得到关于DE的方程，解方程求出DE的长.
25．如图，已知抛物线 y=x2−x−2 交 x 轴于 A 、 B 两点，将该抛物线位于 x 轴下方的部分沿 x 轴翻折，其余部分不变，得到的新图象记为“图象 W ”，图象 W 交 y 轴于点 C .
（1）写出图象 W 位于线段 AB 上方部分对应的函数关系式；
（2）若直线 y=−x+b 与图象 W 有三个交点，请结合图象，直接写出 b 的值；
（3）P 为 x 轴正半轴上一动点，过点 P 作 PM∥y 轴交直线 BC 于点 M ，交图象 W 于点 N ，是否存在这样的点 P ，使 △CMN 与 △OBC 相似？若存在，求出所有符合条件的点 P 的坐标；若不存在，请说明理由.
【答案】（1）解：由翻折可知： C(0，2) .
令 x2−x−2=0 ，解得： x1=−1 ， x2=2 ，
所以， A(−1，0) ， B(2，0) ，
设图象 W 的解析式为 y=a(x+1)(x−2) ，代入 C(0，2) ，解得 a=−1 ，
所以解析式为 y=−x2+x+2(−1≤x≤2)
（2）解：如图

当直线y=-x+b过点C时，b=2；
当直线y=-x+b在x轴上方与抛物线W相切时
∴-x+b=-x2+x+2
整理得x2-2x-2+b=0
b2-4ac=0即4-4（-2+b）=0
解之：b=3.
∴b=2 或 b=3
（3）解：如图1，当 CN∥OB 时， △OBC∽△NMC ，此时， P(1，0) ；
如图2，当 CN∥OB 时， △OBC∽△NMC ，
此时， N 点纵坐标为2， x2−x−2=2 ，解得 x1=1+172 ， x2=1−172 （舍）；
所以 P(1+172，0) ；
如图3，当 ∠NCM=90° 时， △OBC∽△CMN ，此时，直线 CN 的解析式：
y=x+2 ；联立方程组： y=x+2y=x2−x−2 ，解得 x1=1+5 ， x2=1−5 （舍），所以 P(1+5，0) .
因此，综上所述： P 点坐标为 (1，0) 或 (1+172，0) 或 (1+5，0) .
【知识点】二次函数图象的几何变换；相似三角形的判定与性质；二次函数与一次函数的综合应用
【解析】【分析】（1）利用函数解析式可求出点C的坐标，由y=0可得到关于x的方程，解方程求出x的值，可得到点A，B的坐标；利用二次函数的交点式设W的函数解析式为y=a（x+1）（x-2），将点C的坐标代入，可求出a的值，即可得到函数解析式.
（2）分情况讨论：当直线y=-x+b经过点C时，此直线与图象W有三个交点，将点C的坐标代入可求出b的值；当直线y=-x+b位于x轴上方与抛物线W相切时，将两函数联立方程组，可得到关于x的一元二次方程，根据b2-4ac=0，可得到关于b的方程，解方程求出b的值.
（3）分情况讨论：当CN∥OB时可证得△OBC∽△NMC，利用PN∥y轴，可得到点P的坐标；当CN∥OB时，易证△CMN∽△BOC，由y=2，可求出x的值，可得到点P的坐标；当∠NCM=90°时，△OBC∽△CMN，可求出直线CN的函数解析式，将其函数解析式与抛物线联立方程组，解方程组求出x的值，可得到点P的坐标；综上所述，可得到符合题意的点P的坐标.
26．如图，在菱形 ABCD 中， AB=4 ， ∠BAD=60° ，点 P 从点 A 出发，沿线段 AD 以每秒1个单位长度的速度向终点 D 运动，过点 P 作 PQ⊥AB 于点 Q ，作 PM⊥AD 交直线 AB 于点 M ，交直线 BC 于点 F ，设 △PQM 与菱形 ABCD 重叠部分图形的面积为 S （平方单位），点 P 运动时间为 t （秒）.
（1）当点 M 与点 B 重合时，求 t 的值；
（2）当 t 为何值时， △APQ 与 △BMF 全等；
（3）求 S 与 t 的函数关系式；
（4）以线段 PQ 为边，在 PQ 右侧作等边三角形 PQE ，当 2≤t≤4 时，求点 E 运动路径的长.
【答案】（1）解： M 与 B 重合时，

∵∠A=60° ，
∴PA=12AB=2 ，
∴t=2 .
（2）解：①当 0≤t≤2 时，
∵AM=2t ，∴BM=4−2t ，
∵△APQ≌△BMF ，∴AP=BM ，
∴t=4−2t ，∴t=43 .
②当 2 ∵AM=2t ，∴BM=2t−4 ，
∵△APQ≌△BMF ，∴AP=BM ，
∴t=2t−4 ，∴t=4 .
∴t=4 或 t=43 .
（3）解：①当 0≤t≤2 时，

PQ=32t ，∴MQ=32t ，
∴S=S△PQM=338t2 .
②当 2
∵BF=t−2 ， MF=3(t−2) ，
∴S△BFM=32(t−2)2 ，
∴S=S△PQM−S△BFM=−38t2+23t−23 ，
∴S=338t2，0≤t≤2−38t2+23t−23，2 （4）解：连接 AE .
∵△PQE 为正三角形，∴PE=32t ，
在 Rt△APE 中， tan∠PAE=PEPA=32tt=32 ，
∴∠PAE 为定值.
∴E 的运动轨迹为直线，
AE=AP2+PE2=72t ，
当 t=2 时 AE=7 ，
当 t=4 时 AE=27 ，
∴E 的运动路径长为 27−7=7
【知识点】解直角三角形；四边形的综合；四边形-动点问题
【解析】【分析】（1）当点M与点B重合时，利用30°角所对的直角边等于斜边的一半，可求出PA的长，即可得到t的值.
（2）分情况讨论：当0≤t≤2时，利用点的运动方向和速度，可表示出AM，BM的长，利用全等三角形的对应边相等，可证得AP=BM，由此可得到关于t的方程，解方程求出t的值；当2＜t≤4时，可表示出AM，BM的长，利用全等三角形的对应边相等，可得到AP=AM，由此可得到关于t的方程，解方程求出t的值；综上所述可得到t的值.
（3）当0≤t≤2时，利用解直角三角形表示出PQ，MQ的长，再利用三角形的面积公式可得到S与t的函数解析式；当2＜t≤4时，利用解直角三角形可表示出BF，MF的长；利用三角形的面积公式可得到S与t之间的函数解析式；综上所述可得到S与t的函数解析式.
（4）连接AE，利用等边三角形的性质及解直角三角形表示出PE的长，在Rt△APE中利用解直角三角形可得到∠PAE的正切值，可得到∠PAE是定值；从而可得到点E的运动轨迹是直线，利用勾股定理表示出AE的长；再分别求出当t=2和t=4时的AE的长.