2021年下期初三数学竞赛试题

2021下期初三数学竞赛试题

（时量：90分钟   满分：100）

一、选择题（每题4分，共40分.将答案填在表格内）

一、选择题：（每题4分，共40分）

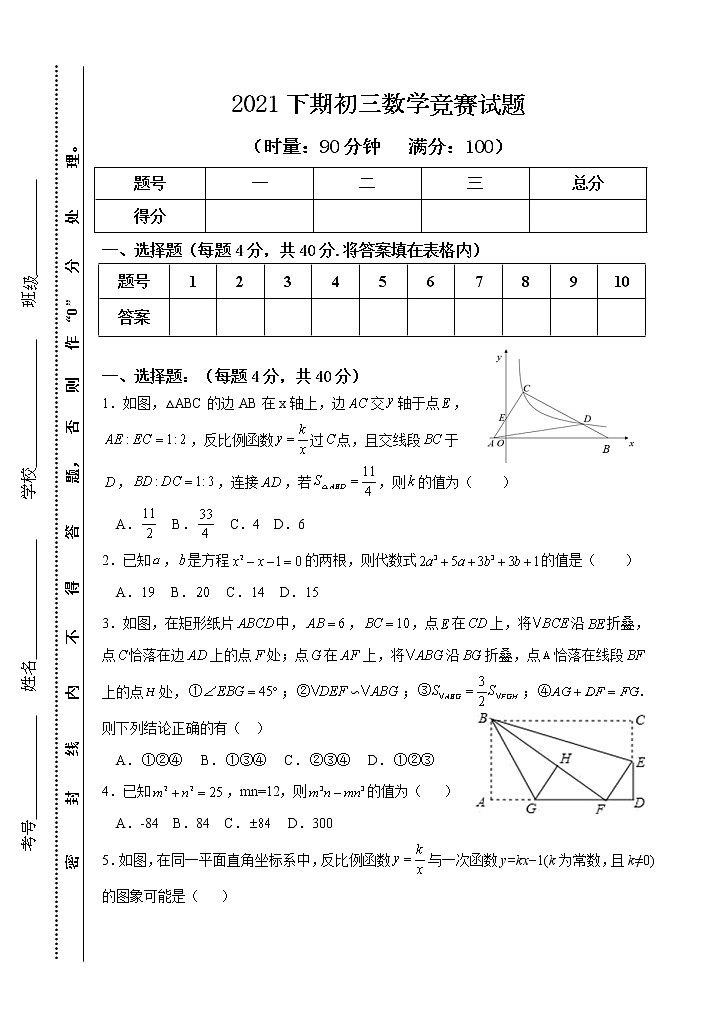
1．如图，△ABC的边AB在x轴上，边交轴于点，

，反比例函数过点，且交线段于

，，连接，若，则的值为（    ）

A．  B．  C．4  D．6

2．已知，是方程的两根，则代数式的值是（    ）

A．  B．  C．  D．

3．如图，在矩形纸片中，，，点在上，将沿折叠，点恰落在边上的点处；点在上，将沿折叠，点恰落在线段上的点处，；∽；；则下列结论正确的有（  ）

A．  B．  C．  D．

4．已知，mn=12，则的值为（   ）

A．-84  B．84  C．  D．300

5．如图，在同一平面直角坐标系中，反比例函数与一次函数y=kx−1(k为常数，且k≠0)的图象可能是（   ）

A． B． C． D．

6．如图，已知AD∥BC，AC与BD相交于点O，点G是BD的中点，过G作GE∥BC交AC于点E，如果AD=1，BC=3，GE：BC等于（      ）

A．1：2  B．1：3  C．1：4  D．2：3

7．若，则的值是（    ）

A．1  B．  C．3  D．无法确定

8．若实数满足方程，那么的值为（    ）

A．-2或4  B．4  C．-2  D．2或-4

9．在中，，为上一动点，

若，，则的最小值为（    ）

A．5  B．10  C．  D．

10．在平面直角坐标系中，点A的坐标为（﹣3，4），那么下列说法正确的是（　　）

A．点A与点C（3，﹣4）关于x轴对称

B．点A与点B（﹣3，﹣4）关于y轴对称

C．点A与点F（3，﹣4）关于原点对称

D．点A与点E（3，4）关于第二象限的平分线对

二、填空题：（每题4分，共20分）

11．如图，直角三角形的直角顶点在坐标原点，∠OAB=30°，

若点A在反比例函数（x>0）的图象上，则经过点B的反比例函数解析式为______．

12．若a，b，c为等腰三角形的三边长且a＝2，其中b，c

是方程x2﹣3x+m＝0的两根．则m＝__________________

13．如图，某测量工作人员的眼睛A与标杆顶端F，铁塔顶

端E在一条直线上，已知此人眼睛距离地面的高为1.6m，标杆

高为3.2m，且BC=1m，CD=5m，则铁塔的高DE=________________m

14．已知是方程的一个根，

θ是三角形的一个内角，那么cosθ的值为________．

15．如图，平行于BC的直线DE把ABC分成面积相等

的两部分，DE＝2，则BC的值为__________．

三、解答题（共4个大题，共40分，解答时要求必要的演算过程或推理步骤）

16．(本题10分)随着全球疫情的扩散，疫苗需求仍存在较大缺口，某制药企业及时引进一条疫苗生产线生产新冠疫苗，开工第一天生产疫苗10000盒，第三天生产疫苗12100盒，若每天增长的百分率相同．

（1）求每天增长的百分率．

（2）经调查发现，1条生产线的最大产能是15000盒/天，若每增加1条生产线，则每条生产线的产能将减少500盒/天，现该厂要保证每天生产疫苗105000盒，在增加产能的同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

17．(本题10分)如图，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知△ABC的边BC长60厘米，高AH为40厘米，矩形DEFG相邻两边DE：EF＝2：3．求矩形DEFG的边DE、EF的长．

18．(本题10分)如图，直线y＝ax＋b与x轴交于点A（4，0），与y轴交于点B（0，﹣2），与反比例函数y＝（x＞0）的图象交于点C（6，m）．

（1）求直线和反比例函数的表达式；

（2）结合图象，请直接写出不等式≥ax＋b的解集；

（3）连接OC，在x轴上找一点P，使S△POC＝2S△AOC，请求出点P的坐标．

19．(本题10分)如果三角形的两个内角α与β满足2α+β=n°，那么我们称这样的三角形为“准n°三角形”．

（1）若△ABC是“准90°三角形”，∠C＞90°，∠A=60°，则∠B=　   　°；

（2）如图①，在△ABC中，∠ACB=120°，AC=4，BC=8．D是BC上一点且△ABD是“准60°三角形”，请求出BD的长．

（3）如图②，在四边形ABCD中，AB=5，CD=6，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准90°三角形”，则对角线AC=                　

宁远县2021下期初三数学竞赛试题答案

1．C；2．D；3．B；4．C；5．B；6．B；7．C；8．B；9．B；10．C

11．；12．或2；13．11.2；14．；15．2

16．解：（1）设每天增长的百分率为，

依题意得：，解得：，（不合题意，舍去）．

答：每天增长的百分率为．

（2）设增加条生产线，则每条生产线的产量为盒/天，

依题意得：，整理得：，

解得：，．又∵要节省投入，∴．

答：应该增加9条生产线．

17．解：

如图，记，的交点为 设，

则，， 四边形为矩形，

，，，，，

，，，

，．

18．解：（1）∵直线经过点和，∴可得方程组

解得∴直线的表达式为．

∵直线与反比例函数y＝（x＞0）的图象交于点，

∴．∴．∴．∴k=6．

∴反比例函数的表达式为．

（2）求不等式的解集相当于从图象上看x取何值时，反比例函数的图象不低于直线的图象．

所以从图象上看，当时，反比例函数的图象不低于直线的图象．

所以不等式的解集是．

（3）∵，，∴OA=4．∴．

∵，∴．

∵点P在x轴上，∴设．∴．

∵，∴．∴，．∴或．

19．解：(1) ∵由“准n°三角形”的定义知：2α+β=n°　∴准90°三角形有：

又∵　∴∠B=15°　故答案为：15                                        

(2)∵△ABD是“准60°三角形”

∴2∠B+∠BAD=60°或∠B+2∠BAD=60°

①当2∠B+∠BAD=60°时，如下图：

∵∠ACB=120°　∴∠B+∠BAC=60°

∴∠B=∠CAD

又∵∠C=∠C　∴△CAD∽△CBA 

∴=　　又∵AC=4，BC=8　∴CD=2  　∴BD=6  

②当∠B+2∠BAD=60°时，作DE⊥AB于E，作DF⊥AC延长线于点F，作AH⊥BC延长线于H，如下图：

∵∠B+2∠BAD=60°，∠B+∠BAC=60°

∴∠BAD=∠CAD　　∴DE=DF

设DC=2a

∵∠ACB=120°

∴在Rt△DCF中, ∠DCF=60°

∴DF=a

∵在Rt△ACH中, ∠ACH=60°，AC=4　　∴∠CAH=30°　　∴CH=2　∴AH=

∵DE⊥AB，AH⊥BC　∴∠BED=∠BHA=90°

又∵∠DBE=∠ABH　　∴△BED∽△BHA  ∴=

在中，

∴　又∵　∴

又∵　∴　∴a=　∴BD=

综上所述，BD=6或BD=

（3）将沿BC翻折得到，如下图：

∴CF=CD=6，∠BCF=∠BCD，∠CBF=∠CBD

∵，∠BCD+∠CBD=90°

∴∠ABD+∠DBC+∠CBF=180°

∴A、B、F三点共线　∴∠FAC+∠ACF=

∴　　∴

∴∠FCB=∠FAC　　

又∵　　∴　∴

∴

∵AF=AB+BF　

设BF=x,则AF=5+x　则　　化简得: 　　

解得：（舍），，即BF=4

在中，AF=9,CF=6

由勾股定理得：AC=

∵

∴