浙江省宁波市三年（2020-2022）小升初数学卷真题分题型分层汇编-19解答题（基础提升）

这是一份浙江省宁波市三年（2020-2022）小升初数学卷真题分题型分层汇编-19解答题（基础提升），共27页。试卷主要包含了5～37，5厘米，5÷2，56+4等内容，欢迎下载使用。
浙江省宁波市三年（2020-2022）小升初数学卷真题分题型分层汇编
19解答题（基础提升）
一、 根据方向和距离确定物体的位置（共1小题）
1. （2022•鄞州区）今年暑假，小艺一家准备从宁波去衢州旅游，小艺从某地图上查到宁波到衢州的信息如图。
（1）从图中可以知道：衢州在宁波的 　 　偏 　 　　 　°方向，直线距离是 　 　千米。
（2）爸爸告诉小艺：一般来说，实际开车距离比图上的直线距离大约要多30%～40%，请你帮小艺算一算：如果汽车平均每小时行80千米，宁波到衢州至少需要多少小时？

二、 比例尺应用题（共1小题）
2. （2021•海曙区）按要求完成。
A.两个年段开展“小发明”制作。五年级段制作了120件，六年级段比五年级段多做了，六年级段比五年级段多做几件？
B.一个机械零件图纸中的比例尺是5：1，这个零件在图纸上的高度是120毫米，实际的高度是多少？
C.百胜鞋城1月和2月共代销了120双鞋，1月和2月的销售比为1：5，那么，1月的销售量是多少？
（1）上述3题中，不能用“120×”来解决的是 　 　。（填字母）
（2）请你把不能用“120×”来解决的问题解答出来。
三、 单式折线统计图（共1小题）
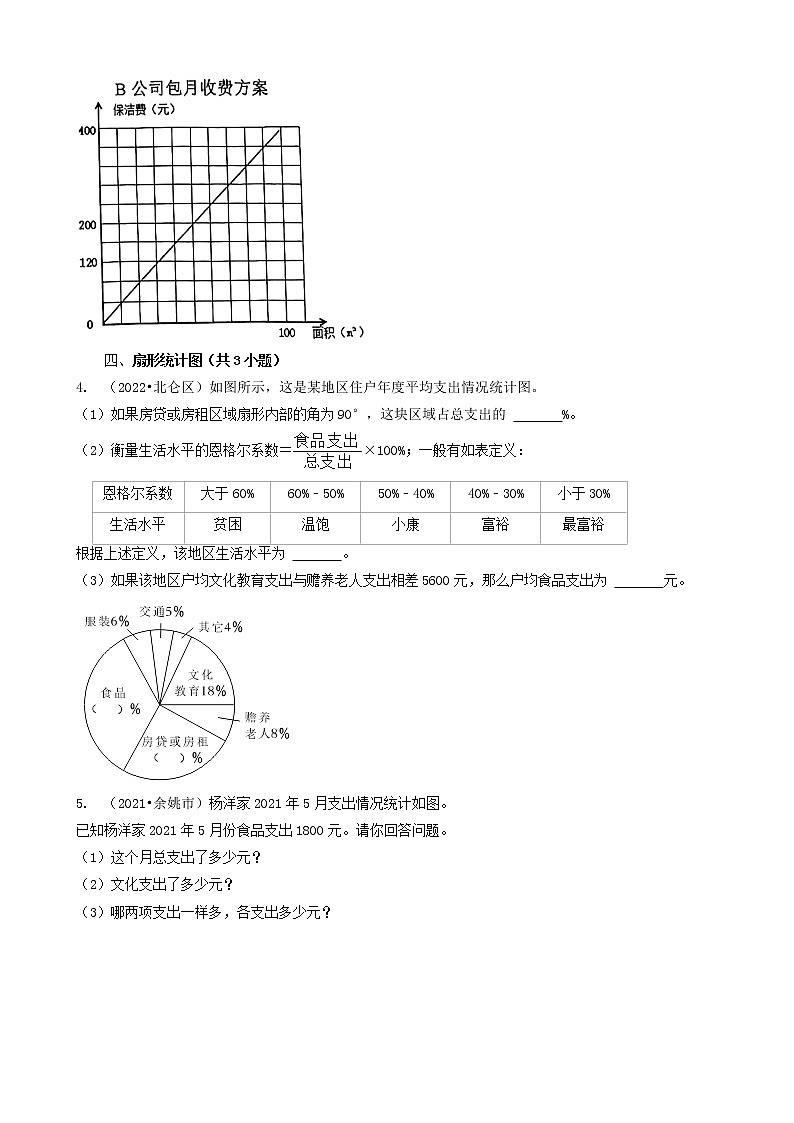
3. （2022•镇海区）新城小学为了使各功能教室更加整洁，公开招聘保洁公司。A、B两家公司各推出了下面的功能教室日常保洁包月收费方案：
A公司包月收费方案
（1）保洁面积不超过1000m2时，每月收取保洁费用4000元。
（2）保洁面积超过1000m2时，在每月收取4000元保洁费的基础上，超过部分每平方米再收取2元保洁费。
新城小学大约有1200m2的功能教室需要保洁，选择哪家公司保洁，包月费用更节省？

四、 扇形统计图（共3小题）
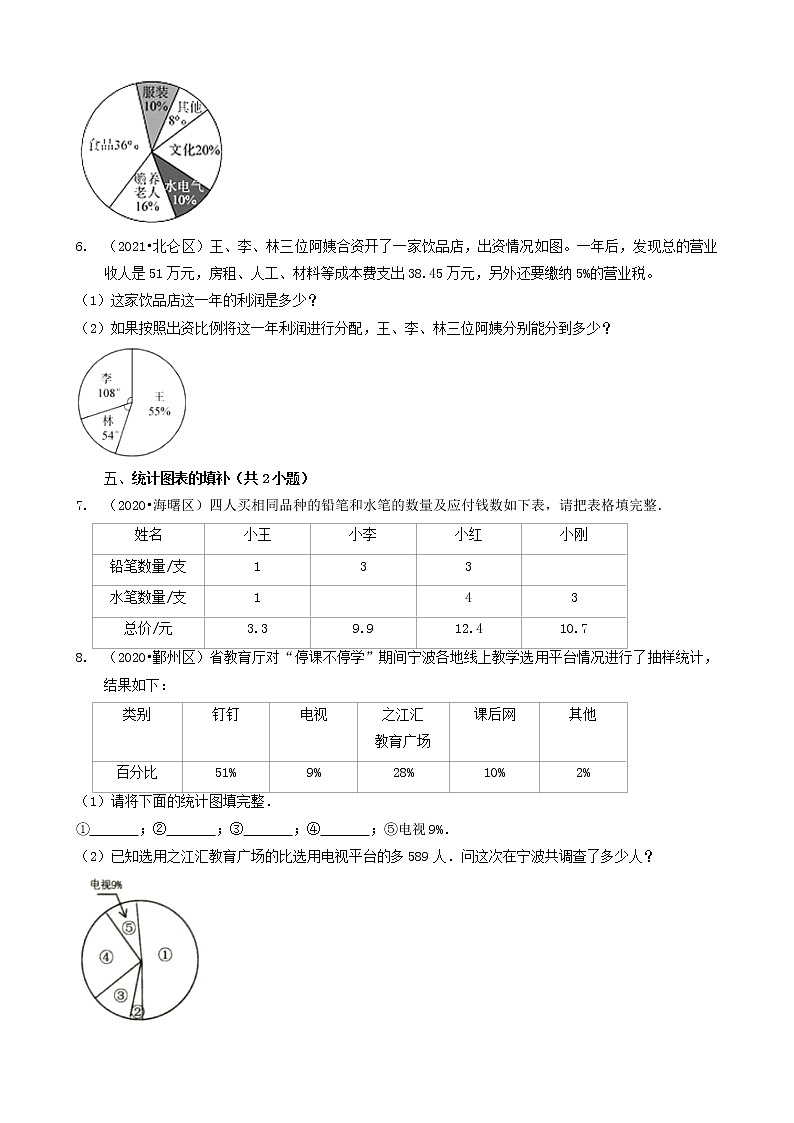
4. （2022•北仑区）如图所示，这是某地区住户年度平均支出情况统计图。
（1）如果房贷或房租区域扇形内部的角为90°，这块区域占总支出的 　 　%。
（2）衡量生活水平的恩格尔系数＝×100%；一般有如表定义：
恩格尔系数
大于60%
60%﹣50%
50%﹣40%
40%﹣30%
小于30%
生活水平
贫困
温饱
小康
富裕
最富裕
根据上述定义，该地区生活水平为 　 　。
（3）如果该地区户均文化教育支出与赡养老人支出相差5600元，那么户均食品支出为 　 　元。

5. （2021•余姚市）杨洋家2021年5月支出情况统计如图。
已知杨洋家2021年5月份食品支出1800元。请你回答问题。
（1）这个月总支出了多少元？
（2）文化支出了多少元？
（3）哪两项支出一样多，各支出多少元？

6. （2021•北仑区）王、李、林三位阿姨合资开了一家饮品店，出资情况如图。一年后，发现总的营业收人是51万元，房租、人工、材料等成本费支出38.45万元，另外还要缴纳5%的营业税。
（1）这家饮品店这一年的利润是多少？
（2）如果按照出资比例将这一年利润进行分配，王、李、林三位阿姨分别能分到多少？

五、 统计图表的填补（共2小题）
7. （2020•海曙区）四人买相同品种的铅笔和水笔的数量及应付钱数如下表，请把表格填完整．
姓名
小王
小李
小红
小刚
铅笔数量/支
1
3
3

水笔数量/支
1

4
3
总价/元
3.3
9.9
12.4
10.7
8. （2020•鄞州区）省教育厅对“停课不停学”期间宁波各地线上教学选用平台情况进行了抽样统计，结果如下：
类别
钉钉
电视
之江汇
教育广场
课后网
其他
百分比
51%
9%
28%
10%
2%
（1）请将下面的统计图填完整．
①　 　；②　 　；③　 　；④　 　；⑤电视9%．
（2）已知选用之江汇教育广场的比选用电视平台的多589人．问这次在宁波共调查了多少人？

六、 从统计图表中获取信息（共3小题）
9. （2022•鄞州区）实验小学开展丰富多彩的劳动教育实践活动。张明将他们年级参加活动的情况绘制成了两幅统计图：

（1）将条形统计图补充完整。
（2）手工编织的占全部人数的 　 　%。
（3）校园保洁的人数比餐饮制作的人数少 　 　%。
（4）关于劳动教育实践活动，你想说些什么？
10. （2021•宁波）下面是一位病人人院后体温记录统计图。

（1）护士每隔 　 　小时给病人测一次体温。
（2）病人体温下降的最快的6小时是从6月 　 　日 　 　时开始的6小时，这6小时体温下降了 　 　摄氏度。
（3）如果体温正常后24小时可以出院，这位病人6月 　 　日 　 　时已具备出院条件。（人的正常体温参考值：36.5～37.5）
（4）如果病人体温达到或超过38摄氏度属于高烧，则这位病人入院以来，高烧持续了 　 　小时。
11. （2021•海曙区）菁菁购买了一个观赏鱼缸，鱼缸的上部安装了一根甲进水管，底部安装了一根乙出水管。为了清洗空鱼缸，上午10时20分，菁菁先打开甲进水管，进水管以每分钟30立方分米的流量向鱼缸里注水。一段时间后她又打开了乙出水管，同步放水。如图显示了鱼缸中水位随着时间变化的情况。
（1）下列是三种规格的鱼缸。
名称
型号
规格（长×宽×缸高）
观赏鱼缸
①
600×450×450mm
②
1000×500×500mm
③
2500×200×300mm
请你从以上信息中推测出菁菁买的是 　 　号鱼缸，并写出推理过程。
（2）如果满缸的水只让乙管出水，多少分钟能够把水全部放完？

七、 分数的巧算（共1小题）
12. （2021•余姚市）先在如图画一画，再计算：++＝
根据你发现的规律，接着画，直接写出得数：
1﹣﹣﹣﹣﹣﹣﹣﹣＝

八、 最优化问题（共1小题）
13. （2021•北仑区）聪聪一家三口一起去电影院看了一场电影《流浪地球》，票价共节省了60元，你知道聪聪一家看的是哪个场次的电影吗？说明理由。
片名
《流浪地球》
票价
每张80元
优惠
办法
上午场
买二送一
下午场
七五折
九、 三角形的内角和（共1小题）
14. （2021•余姚市）观察右图：三角形ABC，延长BC，到D。
（1）发现：∠4＝∠1+∠2他的理由是（在横线上补充完整）：
因为∠4＝180°﹣　 　
而∠1+∠2＝　 　
所以∠4＝∠1+∠2
（2）照这规律，延长三角形一条边，在图上画出一个与∠2十∠3的和相等的角，标为∠5。

十、 圆与组合图形（共1小题）
15. （2020•海曙区）如图圆的直径是4cm，请在圆中画出互相垂直的两条直径，再依次连接圆上的四个点成一个正方形，最后计算出所画正方形的面积．

十一、 长方形、正方形的面积（共1小题）
16. （2021•余姚市）如图四个完全一样的直角三角形，和中心一个小正方形，正好拼成一个大正方形。
（1）如果直角三角形三条边分别是3、4，5厘米，分别求出小、大两个正方形的面积是多少？
（2）如果三角形两条直角边分别是3、7厘米，分别求出小、大两个正方形的面积是多少？

十二、 三角形的周长和面积（共1小题）
17. （2022•江北区）如图一个圆形钟面，圆的周长是314cm。
（1）点A在圆心O的 　 　偏 　 　　 　°的位置上，距离是 　 　cm。
（2）如果点A绕圆心O沿弧线逆时针移动90°后就能到达点B，点B在圆心O的 　 　偏 　 　　 　°的位置上。
（3）请你在图中标出点B的位置，并将O、A、B三点连成一个三角形，列式计算这个三角形的面积。

十三、 组合图形的面积（共6小题）
18. （2022•镇海区）求出如图中阴影部分的面积。

19. （2022•北仑区）求如图阴影部分的面积。（单位：cm）


20. （2021•宁波）如图中，两个正方形的边长分别是6cm和4cm，求阴影部分的面积。

21. （2021•鄞州区）算一算：如图是美术课上小亮设计的一个花瓶图案，这幅图案的周长和面积分别是多少？（小方格的边长是1cm）

22. （2022•慈溪市）计算长方形ABDC绕点D顺时针旋转45°时，CD边扫过的面积。

23. （2021•镇海区）求如图阴影部分的面积。（单位：厘米）

十四、 长方体和正方体的表面积（共1小题）
24. （2020•海曙区）一个纸盒，正好能装进两个完全一样的小长方体，小长方体如图所示，那么这个纸盒的表面积可能是多少平方分米？请画出其中一种示意图并列式计算．（纸盒的厚度忽略不计）

十五、 长方体和正方体的体积（共1小题）
25. （2020•海曙区）有一种酸奶，采用长方体塑封纸盒密封包装．量出外包装长8cm，宽5cm，高13cm，请从数学角度分析该酸奶是否存在虚假说明．

十六、 圆柱的侧面积、表面积和体积（共2小题）
26. （2022•江北区）如图一个装有水的圆柱形容器，现将一个底面半径为5cm，高9cm的圆锥放入容器中，完全浸没在水中，容器的水面比原来升高了多少cm？

27. （2020•鄞州区）长方形绕轴旋转一周，算一算所成图形的体积和表面积．

十七、 圆、圆环的周长（共1小题）
28. （2021•海曙区）如图中圆的周长是25.12厘米，圆的面积与长方形的面积正好相等，则图中阴影部分的周长是多少厘米？（π取3.14）

十八、 圆、圆环的面积（共1小题）
29. （2020•慈溪市）如图正方形AOBC中，点O是圆心，求阴影部分的面积．（单位：厘米）

十九、 组合图形的体积（共2小题）
30. （2022•北仑区）有一种陀螺（如图），上半部分是圆柱，下半部分是圆锥。经过测试，当圆柱的体积与圆锥的体积之比为4：1时，陀螺会转得又稳又快。已知圆锥的底面直径是4厘米，高是1.5厘米。请你算一算，这个陀螺的体积是多少时才能使陀螺转得又稳又快？（π取3.14）

31. （2022•鄞州区）求图形的体积（单位：厘米）。

32. （2021•宁波）如图一个组合体，求它的体积有很多种方法，请在下面推荐的三种方法中选一种你喜欢的，列式解答。
方法1：直接用体积计算公式“底面积×高”。
方法2：看成一个大长方体割去一个小长方体。
方法3：沿中间切开分成左右两个长方体，再把右边的那个移到左上方，正好拼成一个大长方体。
我选择的是第 　 　种方法，解答如下：


二十、 探索某些实物体积的测量方法（共1小题）
33. （2022•镇海区）小东利用两种方法测量石块的体积：

（1）这两种方法相同的地方是：　 　。
（2）请选择你喜欢的一种方法计算这块石块的体积。
参考答案与试题解析
一、 根据方向和距离确定物体的位置（共1小题）
1． （2022•鄞州区）今年暑假，小艺一家准备从宁波去衢州旅游，小艺从某地图上查到宁波到衢州的信息如图。
（1）从图中可以知道：衢州在宁波的 　西　偏 　南　　25　°方向，直线距离是 　240　千米。
（2）爸爸告诉小艺：一般来说，实际开车距离比图上的直线距离大约要多30%～40%，请你帮小艺算一算：如果汽车平均每小时行80千米，宁波到衢州至少需要多少小时？

【解答】解：（1）6×40＝240（千米）
宁波在衢州的东偏北25°方向240千米处，则衢州在宁波的西偏南25°方向，直线距离是240千米。
（2）240×（1+30%）
＝240×1.3
＝312（千米）
312÷80≈4（小时）
答：宁波到衢州至少需要约4小时。
故答案为：西，南25，240。
二、 比例尺应用题（共1小题）
2． （2021•海曙区）按要求完成。
A.两个年段开展“小发明”制作。五年级段制作了120件，六年级段比五年级段多做了，六年级段比五年级段多做几件？
B.一个机械零件图纸中的比例尺是5：1，这个零件在图纸上的高度是120毫米，实际的高度是多少？
C.百胜鞋城1月和2月共代销了120双鞋，1月和2月的销售比为1：5，那么，1月的销售量是多少？
（1）上述3题中，不能用“120×”来解决的是 　C　。（填字母）
（2）请你把不能用“120×”来解决的问题解答出来。
【解答】解：（1）上述3题中，不能用“120×”来解决的是C。
（2）120÷（5+1）×1
＝20×1
＝20（双）
答：1月的销售量是20双。
故答案为：C。
三、 单式折线统计图（共1小题）
3． （2022•镇海区）新城小学为了使各功能教室更加整洁，公开招聘保洁公司。A、B两家公司各推出了下面的功能教室日常保洁包月收费方案：
A公司包月收费方案
（1）保洁面积不超过1000m2时，每月收取保洁费用4000元。
（2）保洁面积超过1000m2时，在每月收取4000元保洁费的基础上，超过部分每平方米再收取2元保洁费。
新城小学大约有1200m2的功能教室需要保洁，选择哪家公司保洁，包月费用更节省？

【解答】解：A公司：因为保洁面积超过1000m2，所以用方案（2）计费。
4000+（1200﹣1000）×2＝4400（元）
B公司：400÷100＝4
1200×4＝4800（元）
4400元＜4800元
答：选择A公司包月费用更节省。
四、 扇形统计图（共3小题）
4． （2022•北仑区）如图所示，这是某地区住户年度平均支出情况统计图。
（1）如果房贷或房租区域扇形内部的角为90°，这块区域占总支出的 　34　%。
（2）衡量生活水平的恩格尔系数＝×100%；一般有如表定义：
恩格尔系数
大于60%
60%﹣50%
50%﹣40%
40%﹣30%
小于30%
生活水平
贫困
温饱
小康
富裕
最富裕
根据上述定义，该地区生活水平为 　富裕　。
（3）如果该地区户均文化教育支出与赡养老人支出相差5600元，那么户均食品支出为 　19040　元。

【解答】解：（1）90°÷360°
＝0.25
＝25%
答：这块区域占总支出的25%。
（2）1﹣（25%+8%+18%+4%+6%+5%）
＝1﹣66%
＝34%
40%＞34%＞30%
答：该地区生活水平为富裕。
（3）5600÷（18%﹣8%）×34%
＝5600÷0.1×0.34
＝56000×0.34
＝19040（元）
答：户均食品支出为19040元。
故答案为：34；富裕；19040。
5． （2021•余姚市）杨洋家2021年5月支出情况统计如图。
已知杨洋家2021年5月份食品支出1800元。请你回答问题。
（1）这个月总支出了多少元？
（2）文化支出了多少元？
（3）哪两项支出一样多，各支出多少元？

【解答】解：（1）1800÷36%＝5000（元）
答：这个月总支出了5000元。
（2）5000×20%＝1000（元）
答：文化支出了1000元。
（3）服装和水电气支出一样多
5000×10%＝500（元）
答：服装和水电气支出一样多，各500元。
6． （2021•北仑区）王、李、林三位阿姨合资开了一家饮品店，出资情况如图。一年后，发现总的营业收人是51万元，房租、人工、材料等成本费支出38.45万元，另外还要缴纳5%的营业税。
（1）这家饮品店这一年的利润是多少？
（2）如果按照出资比例将这一年利润进行分配，王、李、林三位阿姨分别能分到多少？

【解答】解：（1）51﹣38.45﹣51×5%
＝51﹣38.45﹣2.55
＝10（万元）
答：这家饮品店这一年的利润是10万元。
（2）10×55%＝5.5（万元）
10×＝3（万元）
10×＝1.5（万元）
答：王阿姨分别能分到5.5万元，李阿姨分别能分到3万元，林阿姨分别能分到1.5万元。
五、 统计图表的填补（共2小题）
7． （2020•海曙区）四人买相同品种的铅笔和水笔的数量及应付钱数如下表，请把表格填完整．
姓名
小王
小李
小红
小刚
铅笔数量/支
1
3
3

水笔数量/支
1

4
3
总价/元
3.3
9.9
12.4
10.7
【解答】解：12.4﹣3.3×3＝2.5（元）
3.3﹣2.5＝0.8（元）
（9.9﹣0.8×3）÷2.5
＝（9.9﹣2.4）÷2.5
＝7.5÷2.5
＝3（支）
（10.7﹣3×2.5）÷0.8
＝（10.7﹣7.5）÷0.8
＝3.2÷0.8
＝4（支）
填表如下：
姓名
小王
小李
小红
小刚
铅笔数量/支
1
3
3
4
水笔数量/支
1
3
4
3
总价/元
3.3
9.9
12.4
10.7
8． （2020•鄞州区）省教育厅对“停课不停学”期间宁波各地线上教学选用平台情况进行了抽样统计，结果如下：
类别
钉钉
电视
之江汇
教育广场
课后网
其他
百分比
51%
9%
28%
10%
2%
（1）请将下面的统计图填完整．
①　钉钉51%　；②　其他2%　；③　课后网10%　；④　之江汇教育广场28%　；⑤电视9%．
（2）已知选用之江汇教育广场的比选用电视平台的多589人．问这次在宁波共调查了多少人？

【解答】解：（1①钉钉51%；②其他2%；③课后网10%；④之江汇教育广场28%；⑤（2）589÷（28%﹣9%）
＝589÷0.19
＝3100（人）
答：这次在宁波共调查了3100人．
故答案为：①钉钉51%；②其他2%；③课后网10%；④之江汇教育广场28%；⑤
六、 从统计图表中获取信息（共3小题）
9． （2022•鄞州区）实验小学开展丰富多彩的劳动教育实践活动。张明将他们年级参加活动的情况绘制成了两幅统计图：

（1）将条形统计图补充完整。
（2）手工编织的占全部人数的 　20　%。
（3）校园保洁的人数比餐饮制作的人数少 　25　%。
（4）关于劳动教育实践活动，你想说些什么？
【解答】解：（1）40÷40%
＝40÷0.4
＝100（人）
100﹣（40+20+30）
＝100﹣90
＝10（人）
作图如下：

（2）20÷100＝20%
答：手工编织的占全部人数的20%。
（3）（40﹣30）÷40
＝10÷40
＝0.25
＝25%
答：校园保洁的人数比餐饮制作的人数少25%。
（4）答案不唯一。关于劳动教育实践活动，我想说加强劳动教育和实践活动，能够培养学生的动手操作能力，以及与同学们的合作能力。
故答案为：20；25。
10． （2021•宁波）下面是一位病人人院后体温记录统计图。

（1）护士每隔 　6　小时给病人测一次体温。
（2）病人体温下降的最快的6小时是从6月 　1　日 　6　时开始的6小时，这6小时体温下降了 　1.5　摄氏度。
（3）如果体温正常后24小时可以出院，这位病人6月 　3　日 　24　时已具备出院条件。（人的正常体温参考值：36.5～37.5）
（4）如果病人体温达到或超过38摄氏度属于高烧，则这位病人入院以来，高烧持续了 　24　小时。
【解答】解：（1）护士每隔6小时给病人测一次体温。
（2）39.5﹣38＝1.5（摄氏度）
答：病人体温下降的最快的6小时是从6月1日6时开始的6小时，这6小时体温下降了1.5摄氏度。
（3）如果体温正常后24小时可以出院，这位病人6月3日24时已具备出院条件。
（4）如果病人体温达到或超过38摄氏度属于高烧，则这位病人入院以来，高烧持续了24小时。
故答案为：6；1；6；1.5；3，24，24。
11． （2021•海曙区）菁菁购买了一个观赏鱼缸，鱼缸的上部安装了一根甲进水管，底部安装了一根乙出水管。为了清洗空鱼缸，上午10时20分，菁菁先打开甲进水管，进水管以每分钟30立方分米的流量向鱼缸里注水。一段时间后她又打开了乙出水管，同步放水。如图显示了鱼缸中水位随着时间变化的情况。


（1）下列是三种规格的鱼缸。
名称
型号
规格（长×宽×缸高）
观赏鱼缸
①
600×450×450mm
②
1000×500×500mm
③
2500×200×300mm
请你从以上信息中推测出菁菁买的是 　②　号鱼缸，并写出推理过程。
（2）如果满缸的水只让乙管出水，多少分钟能够把水全部放完？

【解答】解：（1）30立方分米＝30000立方厘米
鱼缸底面积应为：30000×5÷30＝5000（平方厘米）＝500000平方毫米
鱼缸①底面积：600×450＝270000（平方毫米）
鱼缸②底面积：1000×500＝500000（平方毫米）
鱼缸③底面积：2500×200＝500000（平方毫米）
只看底面积②、③号鱼缸都可能，但从统计图看，10：30水位达到40厘米，鱼缸③高度为300毫米，即30厘米，水位不可能达到40厘米的水位，所以菁菁买的是②号鱼缸。
（2）500毫米＝50厘米
50÷[30÷5﹣（40﹣30）÷5]
＝50÷[6﹣10÷5]
＝50÷[6﹣2]
＝50÷4
＝12.5（分钟）
答：12.5分钟能够把水全部放完。
故答案为：②。
七、 分数的巧算（共1小题）
12． （2021•余姚市）先在如图画一画，再计算：++＝
根据你发现的规律，接着画，直接写出得数：
1﹣﹣﹣﹣﹣﹣﹣﹣＝

【解答】解：如图：

+++＝

1﹣﹣﹣﹣﹣﹣﹣
＝1﹣（++++++）
＝1﹣
＝
八、 最优化问题（共1小题）
13． （2021•北仑区）聪聪一家三口一起去电影院看了一场电影《流浪地球》，票价共节省了60元，你知道聪聪一家看的是哪个场次的电影吗？说明理由。
片名
《流浪地球》
票价
每张80元
优惠
办法
上午场
买二送一
下午场
七五折
【解答】解：上午场：
买二送一，三口人可以节省了一个人的票钱，
1×80＝80（元）
下午场：
80×（1﹣75%）×3
＝80×25%×3
＝20×3
＝60（元）
60＝60
答：聪聪一家看的是下午场的电影。
九、 三角形的内角和（共1小题）
14． （2021•余姚市）观察右图：三角形ABC，延长BC，到D。
（1）发现：∠4＝∠1+∠2他的理由是（在横线上补充完整）：
因为∠4＝180°﹣　180°﹣∠3　
而∠1+∠2＝　180°﹣∠3　
所以∠4＝∠1+∠2
（2）照这规律，延长三角形一条边，在图上画出一个与∠2十∠3的和相等的角，标为∠5。

【解答】解：（1）因为∠4＝180°﹣∠3
而∠1+∠2＝180°﹣∠3
所以∠1+∠2＝∠4。
（2）延长CA到E，将∠BAE标为∠5或延长BA到E，将∠CAE标为∠5。如图：

故答案为：180°﹣∠3，180°﹣∠3。
十、 圆与组合图形（共1小题）
15． （2020•海曙区）如图圆的直径是4cm，请在圆中画出互相垂直的两条直径，再依次连接圆上的四个点成一个正方形，最后计算出所画正方形的面积．

【解答】解：圆的半径为：4÷2＝2（厘米）
在圆中画出互相垂直的两条直径，再依次连接圆上的四个点成一个正方形如下图所示：

可见，这个正方形是由四个小三角形组成的，且小三角形的面积两条直角边已知，
正方形的面积：4×（2×2÷2）＝8（平方厘米），
答：这个正方形的面积是8平方厘米．
十一、 长方形、正方形的面积（共1小题）
16． （2021•余姚市）如图四个完全一样的直角三角形，和中心一个小正方形，正好拼成一个大正方形。
（1）如果直角三角形三条边分别是3、4，5厘米，分别求出小、大两个正方形的面积是多少？
（2）如果三角形两条直角边分别是3、7厘米，分别求出小、大两个正方形的面积是多少？

【解答】解：（1）小正方形的面积：
（4﹣3）×（4﹣3）
＝1×1
＝1（平方厘米）
大正方形的面积：
5×5＝25（平方厘米）
答：小正方形的面积是1平方厘米，大正方形的面积是25平方厘米。
（2）小正方形的面积：
（7﹣3）×（7﹣3）
＝4×4
＝16（平方厘米）
大正方形的面积：
16+7×3÷2×4
＝16+10.5×4
＝16+42
＝58（平方厘米）
答：小正方形的面积是16平方厘米，大正方形的面积是58平方厘米。
十二、 三角形的周长和面积（共1小题）
17． （2022•江北区）如图一个圆形钟面，圆的周长是314cm。
（1）点A在圆心O的 　北　偏 　东　　30　°的位置上，距离是 　50　cm。
（2）如果点A绕圆心O沿弧线逆时针移动90°后就能到达点B，点B在圆心O的 　北　偏 　西　　60　°的位置上。
（3）请你在图中标出点B的位置，并将O、A、B三点连成一个三角形，列式计算这个三角形的面积。

【解答】解：（1）360÷12＝30°
314÷3.14＝100（cm）
100÷2＝50（cm）
点点A在圆心O的北偏30°的位置上，距离是50cm。
（2）点A绕圆心O沿弧线逆时针移动90°后就能到达点B，指针指向“10”，12到10有2个大格，30°×2＝60°，所以点B在圆心O的北偏西60°的位置上。
（3）
连接O、A、B，AO＝BO＝r，∠AOB＝90°，所以三角形AOB是等腰直角三角形。
50×50÷2
＝2500÷2
＝1250（cm2）
答：这个三角形的面积是1250cm2。
故答案为：北，东，30，50；北，西，60。
十三、 组合图形的面积（共6小题）
18． （2022•镇海区）求出如图中阴影部分的面积。

【解答】解：如图：

8×8÷2÷2
＝64÷2÷2
＝32÷2
＝16（平方分米）
答：阴影部分的面积是16平方分米。
19． （2022•北仑区）求如图阴影部分的面积。（单位：cm）


【解答】解：8÷2＝4（厘米）
×42×3.14＝12.56（平方厘米）
4×4÷2＝8（平方厘米）
12.56﹣8＝4.56（平方厘米）
82×3.14×45÷360＝25.12（平方厘米）
25.12﹣12.56﹣8＝4.56（平方厘米）
4.56+4.56＝9.12（平方厘米）
答：阴影部分面积是9.12平方厘米。
20． （2021•宁波）如图中，两个正方形的边长分别是6cm和4cm，求阴影部分的面积。

【解答】解：3.14×6²×+（4+6）×4÷2﹣（6+4）×4÷2
＝28.26+20﹣20
＝28.26（平方厘米）
答：阴影部分的面积是28.26平方厘米。
21． （2021•鄞州区）算一算：如图是美术课上小亮设计的一个花瓶图案，这幅图案的周长和面积分别是多少？（小方格的边长是1cm）

【解答】解：3.14×2×2+4×2
＝12.56+8
＝20.56（cm）

4×4＝16（cm²）
答：这幅图案的周长是20.56cm，面积是16cm²。
22． 50．（2022•慈溪市）计算长方形ABDC绕点D顺时针旋转45°时，CD边扫过的面积。

【解答】解：CD边扫过的面积即阴影部分面积
圆心角：45÷360＝
阴影面积：×402×π＝628（cm2）
答：CD边扫过的面积628平方厘米。
23． 51．（2021•镇海区）求如图阴影部分的面积。（单位：厘米）

【解答】解：3.14×8×8×﹣8×8÷2
＝50.24﹣32
＝18.24（平方厘米）
答：阴影面积是18.24平方厘米。
十四、 长方体和正方体的表面积（共1小题）
24． （2020•海曙区）一个纸盒，正好能装进两个完全一样的小长方体，小长方体如图所示，那么这个纸盒的表面积可能是多少平方分米？请画出其中一种示意图并列式计算．（纸盒的厚度忽略不计）

【解答】解：如图：

（4×4+4×3+4×3）×2
＝（16+12+12）×2
＝40×2
＝80（平方分米）
（4×2+4×6×2×6）×2
＝（8+24+12）×2
＝44×2
＝88（平方分米）
（8×2+8×3+2×3）×2
＝（16+24+6）×2
＝46×2
＝92（平方分米）
答：这个纸盒的表面积可能是80平方分米、88平方分米、92平方分米．
十五、 长方体和正方体的体积（共1小题）
25． （2020•海曙区）有一种酸奶，采用长方体塑封纸盒密封包装．量出外包装长8cm，宽5cm，高13cm，请从数学角度分析该酸奶是否存在虚假说明．

【解答】解：550毫升＝550立方厘米
8×5×13
＝40×13
＝520（立方厘米）
520立方厘米＜550立方厘米
答：该酸奶存在虚假说明．
十六、 圆柱的侧面积、表面积和体积（共1小题）
26． （2022•江北区）如图一个装有水的圆柱形容器，现将一个底面半径为5cm，高9cm的圆锥放入容器中，完全浸没在水中，容器的水面比原来升高了多少cm？

【解答】解：×3.14×52×9÷[3.14×（20÷2）2]
＝×3.14×25×9÷[3.14×102]
＝235.5÷[3.14×100]
＝235.5÷314
＝0.75（cm）
答：容器的水面比原来升高了0.75cm。
27． 52．（2020•鄞州区）长方形绕轴旋转一周，算一算所成图形的体积和表面积．

【解答】解：以长为轴旋转一周所形成圆柱的底面半径是10厘米，高是20厘米；
体积是：3.14×102×20
＝314×20
＝6280（立方厘米）
表面积是：3.14×102×2+3.14×10×2×20
＝628+1256
＝1884（平方厘米）
答：所成图形的体积是6280立方厘米，表面积是1884平方厘米．
十七、 圆、圆环的周长（共1小题）
28． 48．（2021•海曙区）如图中圆的周长是25.12厘米，圆的面积与长方形的面积正好相等，则图中阴影部分的周长是多少厘米？（π取3.14）

【解答】解：25.12÷3.14÷2＝4（厘米）
3.14×42
＝3.14×16
＝50.24（平方厘米）
50.24÷4＝12.56（厘米）
12.56×2+25.12×
＝25.12+6.28
＝31.4（厘米）
答：阴影部分的周长是31.4厘米。
十八、 圆、圆环的面积（共1小题）
29． 49．（2020•慈溪市）如图正方形AOBC中，点O是圆心，求阴影部分的面积．（单位：厘米）

【解答】解：方法1：（4+4×2）×4÷2﹣4×4÷2﹣×3.14×42
＝24﹣8﹣12.56
＝3.44（平方厘米）
方法2：4×4﹣×3.14×42
＝16﹣12.56
＝3.44（平方厘米）
答：阴影部分的面积是3.44平方厘米．
十九、 组合图形的体积（共2小题）
30． （2022•北仑区）有一种陀螺（如图），上半部分是圆柱，下半部分是圆锥。经过测试，当圆柱的体积与圆锥的体积之比为4：1时，陀螺会转得又稳又快。已知圆锥的底面直径是4厘米，高是1.5厘米。请你算一算，这个陀螺的体积是多少时才能使陀螺转得又稳又快？（π取3.14）

【解答】解：3.14×（4÷2）2×1.5÷
＝3.14×4×1.5÷
＝6.28×5
＝31.4（立方厘米）
答：这个陀螺的体积是31.4立方厘米时才能使陀螺转得又稳又快。
31． （2022•鄞州区）求图形的体积（单位：厘米）。

【解答】解：3.14×22×10×+10×6×2
＝3.14×4×10×+60×2
＝94.2+120
＝214.2（立方厘米）
答：它的体积是214.2立方厘米。
32． （2021•宁波）如图一个组合体，求它的体积有很多种方法，请在下面推荐的三种方法中选一种你喜欢的，列式解答。
方法1：直接用体积计算公式“底面积×高”。
方法2：看成一个大长方体割去一个小长方体。
方法3：沿中间切开分成左右两个长方体，再把右边的那个移到左上方，正好拼成一个大长方体。
我选择的是第 　3　种方法，解答如下：

【解答】解：120×（60﹣30）×（30+15）
＝120×30×45
＝3600×45
＝162000（立方厘米）
答：它的体积是162000立方厘米。
故答案为：3。
二十、 探索某些实物体积的测量方法（共1小题）
33． （2022•镇海区）小东利用两种方法测量石块的体积：

（1）这两种方法相同的地方是：　转化法　。
（2）请选择你喜欢的一种方法计算这块石块的体积。
【解答】解：（1）这两种方法相同的地方是：转化法。
（2）3.14×（8÷2）2×（8﹣6）
＝3.14×16×2
＝100.48（立方厘米）
答：这块石头的体积是100.48立方厘米。
故答案为：转化法，100.48立方厘米。