2021学年3.2 立方根精品ppt课件

这是一份2021学年3.2 立方根精品ppt课件，文件包含湘教版8上数学第三章321《立方根》课件pptx、湘教版8上数学第三章321《立方根》教案docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。
理解掌握立方根的概念，能利用立方根的概念求一个数的立方根，并能用计算器求一个数立方根。
通过平方根和立方引出立方根，然后学习了立方根的概念及求法，并用计算器求一个数的立方根。
开立方与立方的关系，立方根与平方根的区别。
培养学生观察比较能力，逆向思维能力，从实践中总结规律及解题技巧的能力。获得相关数学知识和技能，激发学生学习数学的兴趣。
理解掌握立方根的概念及求法，并能用计算器求一个无理数的近似值。
1、已知:2m+2的平方根是±4，3m+n+1的平方根是±5，求m+2n的值.
∴m+2n=7+2×3=13
∴a+6=0, b2-2b-3=0
∴a=-6, b2-2b=3
∴2b2-4b-a=2(b2-2b)-a=2×3-(-6)=12
解：∵32＜11＜42
∴a-b=3-4=-1
求一个开不尽方的算术平方根的整数部分，只需看被开方数处于哪两个连续自然数的平方之间。
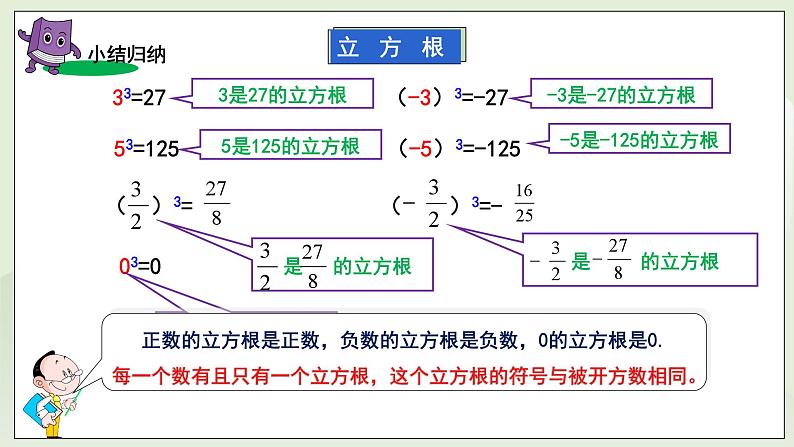
（ ）3=-27
（ ）3=27
（ ）3=125
（ ）3=-125
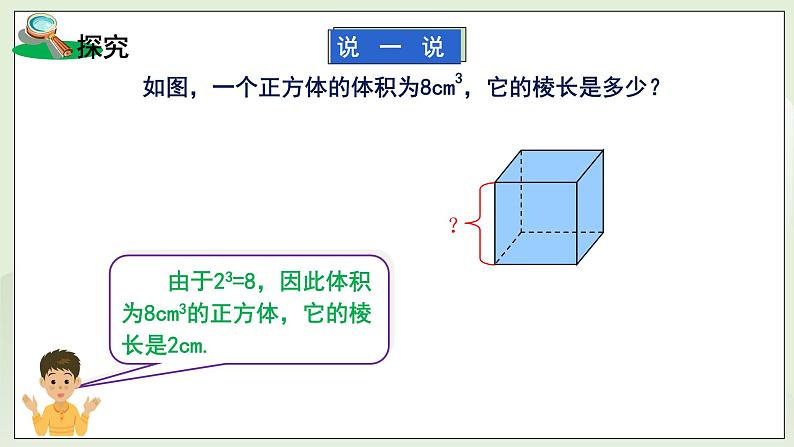
如图，一个正方体的体积为8cm3，它的棱长是多少？
由于23=8，因此体积为8cm3的正方体，它的棱长是2cm.
如果一个数b，使得b3=a，那么我们把b叫作a的一个立方根，也叫作三次方根.
一个正数有几个立方根？0的立方根是多少？负数有立方根吗？
-5是-125的立方根
求一个数的立方根的运算，叫作开立方.
开立方与立方也互为逆运算，根据这种关系，可以求一个数的立方根.
27-27125-125
一般地，在迄今为止我们所认识的数中，每一个数有且只有一个立方根；
利用计算器可以求一个数的立方根或立方根的近似值.
1、一个正数有一个正的立方根
3、一个负数有一个负的立方根
任何数都有且只有一个立方根,但只有非负数有平方根.且正数有两个互为相反的平方根,0的平方根是0.
例2 用计算器求下列各数的立方根: 343， -1.331.
实际上，许多有理数的立方根都是无理数，
但我们可以用有理数来近似地表示它们.
开不尽方的立方根也是无理数！
显示：1.25992105
1. 求下列各数的立方根： 1， ， -0.125 .
2. 用计算器求下列各数的立方根： -1000， 216， -3.375 .
3. 用计算器求下列各数的近似值（精确到0.001）
如果b3=a，那么b叫作a的一个立方根.
每一个数有且只有一个立方根，这个立方根的符号与被开方数相同。
开不尽方的立方根也是无理数.
课作：P114 习题3.2 第3、4题家作：P114 习题3.2 第1、2、5、6、7题并预习课本第116~118页