
苏科版初中数学八年级上册期中测试卷(标准难度)(含答案解析)
展开苏科版初中数学八年级上册期中测试卷
考试范围:第一.二.三章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
- 如图已知,,,则判定和全等的依据是( )
A. B. C. D.
- 如图,已知线段米,于点,米,射线于,点从点向运动,每秒走米,点从点向运动,每秒走米,、同时从出发,则出发秒后,在线段上有一点,使与全等,则的值为( )
A. B. C. 或 D. 或
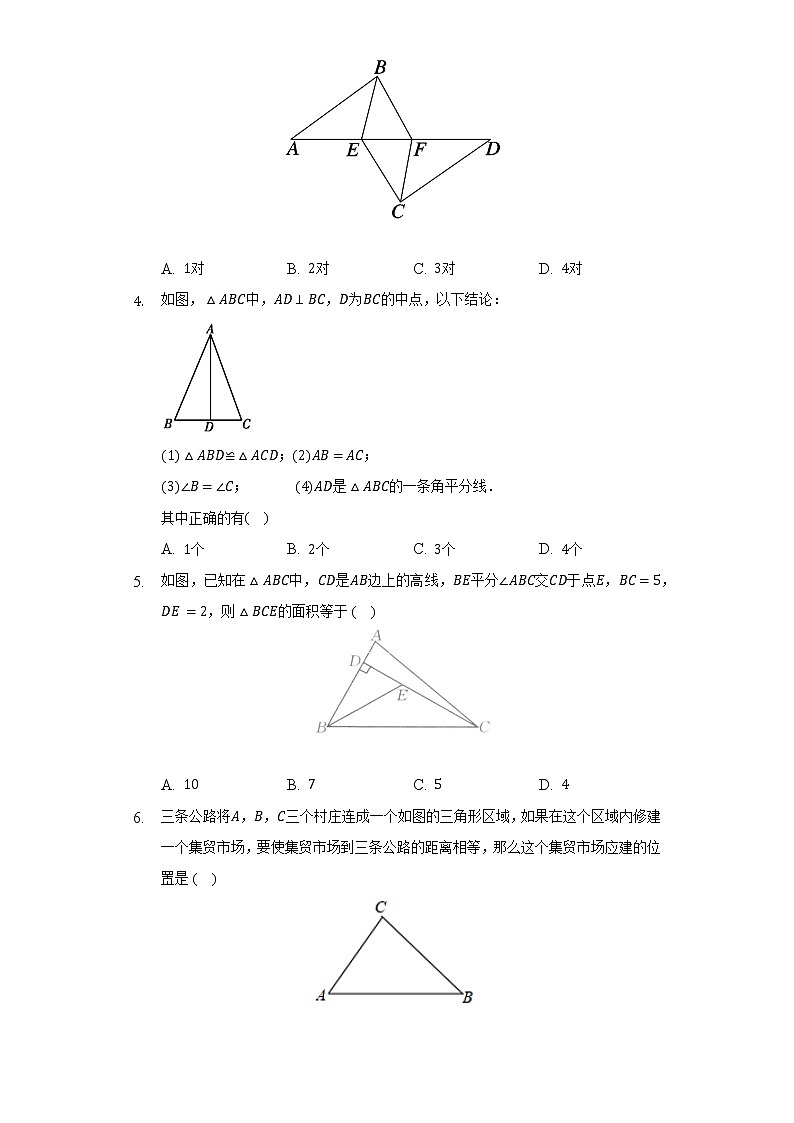
- 如图,已知,,,则图中的全等三角形有( )
A. 对 B. 对 C. 对 D. 对
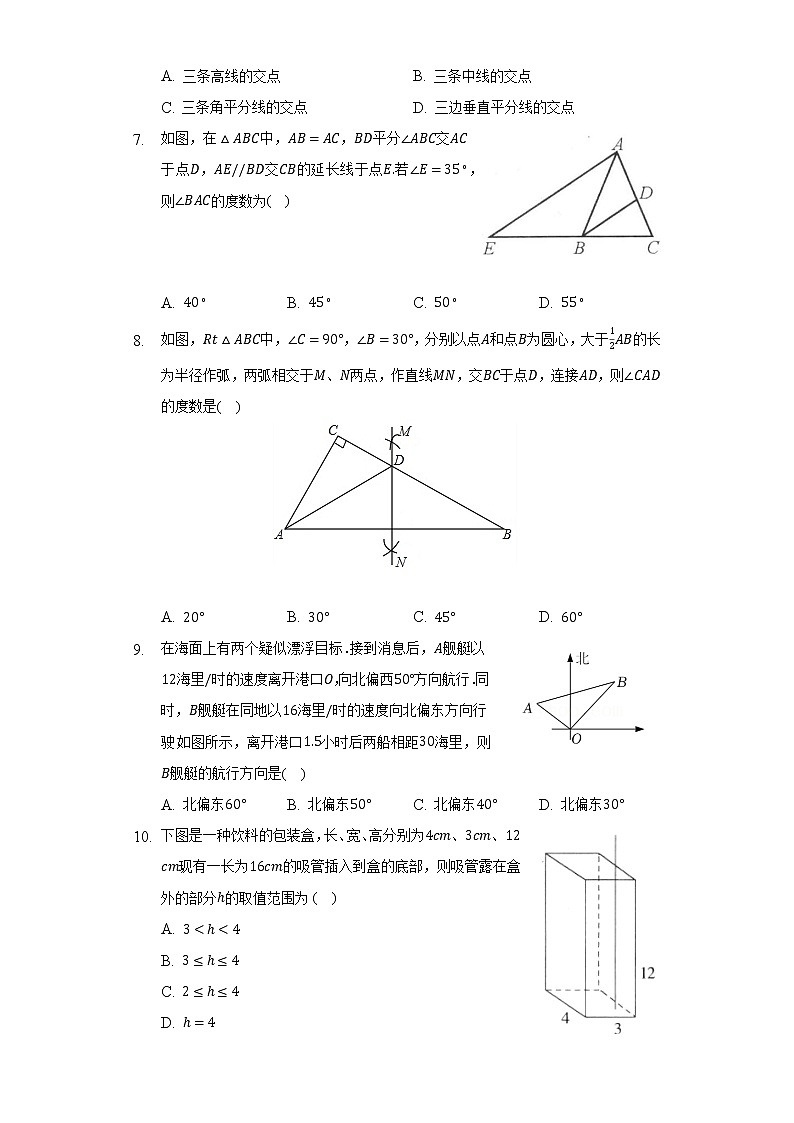
- 如图,中,,为的中点,以下结论:
≌;;
; 是的一条角平分线.
其中正确的有( )
A. 个 B. 个 C. 个 D. 个
- 如图,已知在中,是边上的高线,平分交于点,,,则的面积等于( )
A. B. C. D.
- 三条公路将,,三个村庄连成一个如图的三角形区域,如果在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,那么这个集贸市场应建的位置是( )
A. 三条高线的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
- 如图,在中,,平分交于点,交的延长线于点若,则的度数为( )
A. B. C. D.
- 如图,中,,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于、两点,作直线,交于点,连接,则的度数是( )
A. B. C. D.
- 在海面上有两个疑似漂浮目标.接到消息后,舰艇以海里时的速度离开港口,向北偏西方向航行.同时,舰艇在同地以海里时的速度向北偏东方向行驶,如图所示,离开港口小时后两船相距海里,则舰艇的航行方向是( )
A. 北偏东 B. 北偏东 C. 北偏东 D. 北偏东
- 下图是一种饮料的包装盒,长、宽、高分别为、、,现有一长为的吸管插入到盒的底部,则吸管露在盒外的部分的取值范围为( )
A.
B.
C.
D.
- 如图,在中,,以为圆心,任意长为半径画弧,分别交,于点,,再分别以,为圆心,大于长为半径画弧,两弧交于点,作射线,交于点已知,,则的长为( )
A. B. C. D.
- 如图是高空秋千的示意图,小明从起始位置点处绕着点经过最低点最终荡到最高点处,若,点与点的高度差米,水平距离米,则点与点的高度差为米.( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
- 已知:如图,在中,,,,动点从点出发沿射线以的速度移动,设运动的时间为秒.______时为直角三角形.
- 如图,已知≌,,且,,点在上,则的度数为 .
- 如图,,,于,于,,,则为________.
- 如图,在中,是的垂直平分线.若,的周长为,则的周长为______.
三、解答题(本大题共9小题,共72.0分)
- 如图,已知,,在线段上,与交于点,且,求证:≌.
- 如图,,,,,与交于点.
求证:;
求的度数.
- 如图,,,点在边上,,和相交于点试说明:≌.
- 如图,在的正方形网格中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”.是一个格点三角形,请你在图中分别画出一个与成轴对称的格点三角形,并将所画三角形涂上阴影.
- 如图,在中,,点,,分别在,,边上,且,.
求证:是等腰三角形;
当时,求的度数.
- 如图,中,,若和分别垂直平分和.
求的度数.
若周长为,长为,求的长.
- 如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出米,然后把风筝线沿直线向后拉开米,发现风筝线末端刚好接触地面如图为示意图请你帮小旭求出风筝距离地面的高度.
- 八年级班的小明和小亮同学学了“勾股定理”之后,为了测得图中风筝的高度,他们进行了如下操作:
测得的长为米注:;
根据手中剩余线的长度计算出风筝线的长为米;
牵线放风筝的小明身高米.
求风筝的高度.
过点作,垂足为,求、.
- 如图所示,折叠长方形一边,点落在边的点处,已知,,
求与的长;
求的长.
答案和解析
1.【答案】
【解析】,,
.
在和中,
故选D.
2.【答案】
【解析】解:当≌时,,即,
解得:;
当≌时,米,
此时所用时间为秒,米,不合题意,舍去;
综上,出发秒后,在线段上有一点,使与全等.
故选B.
分两种情况考虑:当≌时与当≌时,根据全等三角形的性质即可确定出时间.
此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法以及分类讨论是解本题的关键.
3.【答案】
【解析】
【分析】
本题主要考查全等三角形的判定,常用的判定方法有,,,,等.做题时要根据已知结合判定方法,由易到难,循序渐进地找寻,做到不重不漏.
分别利用,,来判定≌,≌,≌.
【解答】
解:,
,
,,
≌,
,,
,
,
≌,
,
,
,
即,
≌,
全等三角形共有三对.
故选C.
4.【答案】
【解析】
【分析】
本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即、、、,及全等三角形性质的运用.
先运用证明≌,再得≌ACD正确;AC正确;C正确;是的角平分线.
【解答】
解:、、,
≌ACD正确;
AC正确;
C正确;
是的角平分线.
故选D.
5.【答案】
【解析】
【分析】
此题主要考查角平分线的性质定理和三角形面积公式,根据角平分线上一点,到这个角两边的距离相等,可知三角形中边上的高为长,进而根据三角形面积公式计算即可.
【解答】
解:作,垂足为,
是边上的高线,平分,交于点,
,
,
.
故选C.
6.【答案】
【解析】
【分析】
根据角平分线上的点到角的两边的距离相等解答即可。
【解答】
解:在这个区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,根据角平分线的性质,集贸市场应建在、、的角平分线的交点处。
故选C。
7.【答案】
【解析】略
8.【答案】
【解析】解:在中,,,
,
由作图可知为的中垂线,
,
,
,
故选:.
根据三角形内角和定理求得,由中垂线性质知,即,从而得出答案.
本题主要考查作图基本作图,线段垂直平分线的概念及其性质,熟练掌握中垂线的作图和性质是解题的关键.
9.【答案】
【解析】
【分析】
本题考查的是勾股定理的逆定理的应用和方位角的知识,根据题意判断出是直角三角形是解决问题的关键.
根据勾股定理的逆定理判断是直角三角形,求出的度数即可.
【解答】
解:
由题意得,海里,海里,
又海里,
,即
,
,
,
则舰艇的航行方向是北偏东,
故选:.
10.【答案】
【解析】解:当吸管放进包装盒且垂直于包装盒底面时露在盒外的长度最长,最长为.
露出部分最短时,包装盒内的吸管与底面对角线和高正好组成直角三角形,
底面对角线长为,高为设包装盒里吸管长为,则,
所以,
所以露在包装盒外的吸管的长度最短为.
则吸管露在盒外的部分的取值范围为
故选:.
11.【答案】
【解析】
【分析】
此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确得出的长是解题关键.
直接利用基本作图方法得出是的平分线,进而结合全等三角形的判定与性质得出,再利用勾股定理得出的长.
【解答】
解:过点作于点,
由作图方法可得出是的平分线,
,,
,
在和中,,
≌,
,
在中,,,
,
设,则,
故在中,
,
即,
解得:,
即的长为:.
故选:.
12.【答案】
【解析】解:作于,于,
,
,
,
在与中,
,
≌,
米,
设米,
在中,,即,
解得.
则米.
故选:.
13.【答案】或
【解析】解:在中,,
,
由题意知,
当为直角时,点与点重合,,即,;
当为直角时,,,,
在中,
,
在中,,
即:,
解得:,
故当为直角三角形时,或,
故答案为:或
当为直角三角形时,分两种情况:当为直角时,当为直角时,分别求出此时的值即可.
本题考查了勾股定理,解答本题的关键是掌握勾股定理,以及分情况讨论,注意不要漏解.
14.【答案】
【解析】解:≌,
,,
,
,
,
,
.
,
.
故答案为:.
先由≌,根据全等三角形的性质得出,,由,得出,等量代换得到,那么,于是由三角形内角和定理求出,于是.
本题考查了全等三角形的性质,平行线的判定与性质,三角形内角和定理,求出是解题的关键.
15.【答案】
【解析】
【分析】
本题考查了三角形的面积,全等三角形的判定与性质,易得,从而利用证得,得到,,从而得到,然后利用三角形面积公式计算即可.
【解答】
解:,
,
于,
,
,
又,,
,
,,
,
.
16.【答案】
【解析】
【分析】
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线的性质是解题的关键.
由线段的垂直平分线的性质可得,,从而可得答案.
【解答】
解:是的垂直平分线,,
,,
,
的周长.
故答案为.
17.【答案】证明:,
,即,
,
与都为直角三角形,
在和中,
≌.
【解析】此题考查了直角三角形全等的判定,解题关键是由通过等量代换得到.
由通过等量代换得到,结合,根据直角三角形全等的判定的方法即可证明.
18.【答案】解:,,
,
,
在和中,
,
≌,
;
如图,,
,
≌,
,
,
,
.
【解析】本题考查全等三角形的判定和性质,三角形内角和定理,三角形外角定理,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
先证明,再证明≌便可得;
由全等三角形得,由,推出,可得.
19.【答案】解:因为,,,,
所以.
因为,
所以.
所以.
在和中,
所以≌.
【解析】略
20.【答案】解:答案不唯一,如图所示.
【解析】根据对称图形关于某直线对称,找出不同的对称轴,画出不同的图形,对称轴可以随意确定,因为只要根据你确定的对称轴去画另一半对称图形,那这两个图形一定是轴对称图形.
本题主要考查的是利用轴对称设计图案,掌握轴对称图形的性质是解题的解题的关键.
21.【答案】证明:,
.
在和中,
≌.
是等腰三角形.
解:,
.
又≌,
.
.
【解析】本题主要考查等腰三角形的判定和性质,全等三角形的判定和性质.
要证明是等腰三角形,可先证的边、所在的两个三角形和全等,根据已知条件,得,易用得,进而得到结论;
由、得,由全等三角形的性质得到,所以,即可得解.
22.【答案】解:设,,,
和分别垂直平分和,
,,
,,
,
,
即,,
,
;
的周长为,
,
,,
,
即,
,
,
.
【解析】设,,,根据线段垂直平分线的性质得:,,由等腰三角形的性质得:,,再由三角形内角和定理相加可得结论;
根据周长为,列等式为,由等量代换得,可得的长.
本题主要考查线段垂直平分线的性质,三角形的周长和内角和定理等知识,关键在于根据题意推出,,正确的进行等量代换.
23.【答案】解:设,则,
由图可得,,,
中,,
即,
解得,
答:风筝距离地面的高度为米.
【解析】本题主要考查了勾股定理的应用,在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.设,则,依据勾股定理即可得到方程,进而得出风筝距离地面的高度.
24.【答案】解:在中,由勾股定理,得.
米
米;
由
得米,
在中,,
即米.
【解析】本题考查了勾股定理的应用,熟悉勾股定理,能从实际问题中抽象出勾股定理是解题的关键.
利用勾股定理求出的长,再加上的长度,即可求出的高度;
根据三角形的面积和勾股定理即可得到结论.
25.【答案】解:折叠后的图形是,
,.
,
.
又,在中,根据勾股定理,得
,
,
;
设的长为,则.
在中,根据勾股定理,得:,
,
即,
化简,得,
,
故EC的长为.
【解析】本题主要考查了勾股定理,折叠问题,解题时常设要求的线段长为,然后根据折叠的性质用含的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.
由图形翻折变换的性质可知,,在中利用勾股定理即可求解,再由厘米可得出的长度;
将的长设为,得出,在中,根据勾股定理列出方程求解即可.
苏科版初中数学八年级上册期末测试卷(标准难度)(含答案解析): 这是一份苏科版初中数学八年级上册期末测试卷(标准难度)(含答案解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
苏科版初中数学九年级上册期中测试卷(标准难度)(含答案解析): 这是一份苏科版初中数学九年级上册期中测试卷(标准难度)(含答案解析),共21页。试卷主要包含了二章等内容,欢迎下载使用。
苏科版初中数学八年级上册期中测试卷(标准难度)(含答案解析): 这是一份苏科版初中数学八年级上册期中测试卷(标准难度)(含答案解析),共21页。












