沪科版九年级上册第22章 相似形综合与测试单元测试同步练习题

这是一份沪科版九年级上册第22章 相似形综合与测试单元测试同步练习题，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共12小题，共36.0分）
如果a：b=3：2，且b是a、c的比例中项，那么b：c等于( )
A. 4：3B. 3：4C. 2：3D. 3：2
如图：AB//CD//EF，AD：DF=3：1，BE=12，那么CE的长为( )
A. 3
B. 4
C. 5
D. 6
如图，点P在△ABC的边AC上，若要判定△ABP∽△ACB，则下列添加的条件不正确的是( )
A. ∠ABP=∠CB. ∠APB=∠ABC
C. APAB=ABACD. ABBP=ACAB
如图，在△ABC中，∠ABC=90°，以点A为圆心，以AB的长为半径作弧交AC于点D，连接BD，再分别以点B，D为圆心，大于12BD的长为半径作弧，两弧交于点P，作射线AP交BC于点E，连接DE，则下列结论正确的是( )
A. DE垂直平分ACB. △ABE∽△CBA
C. BD2=BC⋅BED. CE⋅AB=BE⋅CA
如图，已知△ACD∽△ADB，AC=4，AD=2，则AB的长为( )
A. 1
B. 2
C. 3
D. 4
已知△ABC∽△DEF，ABDE=12，若BC=2，则EF=( )
A. 4B. 6C. 8D. 16
如图，△ABC与△DEF位似，点O为位似中心，相似比为2：3.若△ABC的周长为4，则△DEF的周长是( )
A. 4B. 6C. 9D. 16
如图，在直角坐标系中，△OAB的顶点为O(0,0)，A(4,3)，B(3,0).以点O为位似中心，在第三象限内作与△OAB的位似比为13的位似图形△OCD，则点C坐标( )
A. (−1,−1)B. (−43,−1)C. (−1,−43)D. (−2,−1)
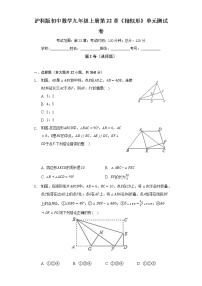
如图，某“综合与实践”小组为测量河两岸A，P两点间的距离，在点A所在岸边的平地上取点B，C，D，使A，B，C在同一条直线上，且AC⊥AP；使CD⊥AC且P，B，D三点在同一条直线上．若测得AB=10m，BC=2m，CD=6m，则A，P两点间的距离为( )
A. 60mB. 40mC. 30mD. 20m
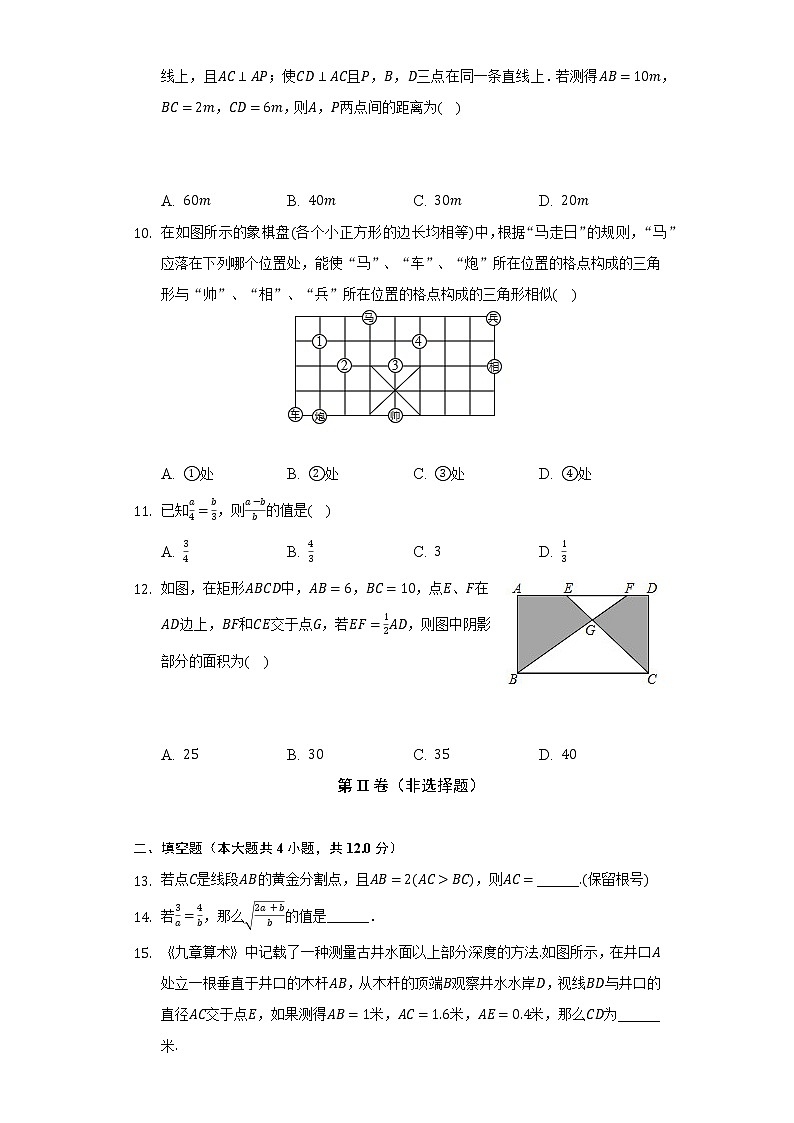
在如图所示的象棋盘(各个小正方形的边长均相等)中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似( )
A. ①处B. ②处C. ③处D. ④处
已知a4=b3，则a−bb的值是( )
A. 34B. 43C. 3D. 13
如图，在矩形ABCD中，AB=6，BC=10，点E、F在AD边上，BF和CE交于点G，若EF=12AD，则图中阴影部分的面积为( )
A. 25B. 30C. 35D. 40
第II卷（非选择题）
二、填空题（本大题共4小题，共12.0分）
若点C是线段AB的黄金分割点，且AB=2(AC>BC)，则AC=______.(保留根号)
若3a=4b，那么2a+bb的值是______．
《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示，在井口A处立一根垂直于井口的木杆AB，从木杆的顶端B观察井水水岸D，视线BD与井口的直径AC交于点E，如果测得AB=1米，AC=1.6米，AE=0.4米，那么CD为______ 米.
如图是一位同学用激光笔测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，若AB⊥BD，CD⊥BD，测得AB=1.5m，BP=2m，PD=6m，则该古城墙的高度CD是______m.
三、解答题（本大题共9小题，共72.0分）
若k=a−2bc=b−2ca=c−2ab，且a+b+c≠0，求k的值．
已知：如图，点D、E、F分别在△ABC的边AB、AC、BC上，DF//AC，BD=2AD，AE=2EC．
(1)如果AB=2AC，求证：四边形ADFE是菱形；
(2)如果AB=2AC，且BC=1，联结DE，求DE的长．
如图，在四边形ABCD中，点E是对角线AC上一点，且ABAC=AEAD=BECD．
(1)若∠DAE=22°，求∠BAD的度数；
(2)判断△ADE与△ACB是否相似，并说明理由．
如图，在△ABC中，AB=AC，点P在BC上．
(1)求作：△PCD，使点D在AC上，且△PCD∽△ABP；(要求：尺规作图，保留作图痕迹，不写作法)
(2)在(1)的条件下，若∠APC=2∠ABC.求证：PD//AB．
如图，已知正方形ABCD，以AB为边在正方形外作等边△ABE，过点E作EF⊥AB与边AB、CD分别交于点F、点G，点O在线段EG上，且DO=CD．
(1)求证：AE//DO；
(2)联结AO、DE，DE分别交AO、AB于点M、Q，求证：EQAD=EFDM．
已知：如图，在矩形ABCD中，点E在边AD的延长线上，DE=DC，联结BE，分别交边DC、对角线AC于点F、G，AD=FD．
(1)求证：AC⊥BE；
(2)求证：CFDF=ACBE．
如图、在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(4,1)，B(2,3)，C(1,2)．
(1)画出与△ABC关于y轴对称的△A1B1C1；
(2)以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2：1，并写出点B2的坐标．
小豪为了测量某塔高度，把镜子放在离塔(AB)50m的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到塔尖A，再测得DE=2.4m，小豪目高CD=1.68m，求塔的高度AB．
雨过天晴，小李急忙跑到室外呼吸新鲜空气，广场上E处有一处积水，如图，若小李站在D处距积水2米，他正好从水面上看到距他约10米的前方一棵树的顶端A的影子已知点D、E、B在同一直线上，AB⊥BD，CD⊥BD，小李的眼睛到地面的距离CD为1.6米，求树AB的高．(∠CED=AEB，积水水面大小忽略不计)
答案和解析
1.【答案】D
【解析】
【分析】
根据比例中项的概念可得a：b=b：c，则可求得b：c的值．
本题考查了比例中项的概念．在线段a，b，c中，若b2=ac，则b是a，c的比例中项．
【解答】
解：∵a：b=3：2，b是a和c的比例中项，
即a：b=b：c，
∴b：c=3：2．
故选D．
2.【答案】A
【解析】解：∵AB//CD//EF，
∴BCCE=ADDF=3，
∴BC=3CE，
∴CE=14BE=14×12=3，
故选：A．
根据平行线分线段成比例定理得到比例式，再根据AD：DF=3：1，BE=12，可计算出CE的长．
本题考查了平行线分线段成比例定理，关键是掌握：三条平行线截两条直线，所得的对应线段成比例．
3.【答案】D
【解析】解：在△ABP和△ACB中，∠BAP=∠CAB，
A、当∠ABP=∠C时，满足两组角对应相等，可判断△ABP∽△ACB，故A不符合题意；
B、当∠APB=∠ABC时，满足两组角对应相等，可判断△ABP∽△ACB，故B不符合题意；
C、当APAB=ABAC时，满足两边对应成比例且夹角相等，可判断△ABP∽△ACB，故C不符合题意；
D、当ABBP=ACAB时，其夹角不相等，则不能判断△ABP∽△ACB，故D符合题意；
故选：D．
根据相似三角形的判定方法，逐项判断即可．
本题主要考查相似三角形的判定，掌握相似三角形的判定方法是解题的关键，即在两个三角形中，满足三边对应成比例、两边对应成比例且夹角相等或两组角对应相等，则这两个三角形相似．
4.【答案】D
【解析】解：由题意可得AB=AD，AP平分∠BAC，
∴AE垂直平分BD，
∴BE=DE，
在△ABE和△ADE中，
AB=ADAE=AEBE=DE，
∴△ABE≌△ADE(SSS)，
∴∠ABE=∠ADE=90°，
又∵∠C=∠C，
∴△ABC∽△EDC，
∴CEAC=DEAB，
∴CE⋅AB=BE⋅CA，
故选D．
由“SSS”可证△ABE≌△ADE，可得∠ABE=∠ADE=90°，可证△ABC∽△EDC，可得结论．
本题考查了相似三角形的判定，全等三角形的性质，证明三角形相似是解题的关键．
5.【答案】A
【解析】解：∵△ACD∽△ADB，
∴ACAD=ADAB，
∴AB=AD2AC=1，
故选：A．
根据相似三角形的性质列出比例式，代入计算即可．
本题考查的是相似三角形的性质，掌握相似三角形的对应边的比相等是解题的关键．
6.【答案】A
【解析】解：∵△ABC∽△DEF，
∴ABDE=BCEF，
∵ABDE=12，BC=2，
∴2EF=12，
∴EF=4，
故选：A．
利用相似三角形的性质可得ABDE=BCEF，代入即可得出EF的长．
本题主要考查了相似三角形的性质，熟练掌握相似三角形的对应边成比例是解题的关键．
7.【答案】B
【解析】解：∵△ABC与△DEF位似，相似比为2：3．
∴C△ABC：C△DEF=2：3，
∵△ABC的周长为4，
∴△DEF的周长是6，
故选：B．
根据位似图形是相似图形，相似三角形的周长比等于相似比，可以求得△DEF的周长．
本题考查位似变换，解答本题的关键是明确相似三角形的周长比等于相似比．
8.【答案】B
【解析】解：∵以点O为位似中心，位似比为13，
而A (4,3)，
∴A点的对应点C的坐标为(−43,−1)．
故选：B．
根据关于以原点为位似中心的对应点的坐标的关系，把A点的横纵坐标都乘以−13即可．
本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，位似比为k，那么位似图形对应点的坐标的比等于k或−k．
9.【答案】C
【解析】解：∵AP⊥AC，CD⊥AC，
∴∠A=∠C=90°，
∵∠ABP=∠CBD，
∴△APB∽△DCB，
∴ABBC=APDC，
∵AB=10m，BC=2m，CD=6m，
∴AP=AB⋅DCBC=10×62=30(m)．
故选：C．
由垂直的定义得到一对直角相等，再由一对对顶角相等，利用两角相等的两个三角形相似得到三角形APB与三角形DCB相似，由相似得比例求出所求即可．
此题考查了相似三角形的应用，熟练掌握相似三角形的判定与性质是解本题的关键．
10.【答案】B
【解析】
【分析】
本题考查了相似三角形的知识，解题的关键是利用勾股定理求得三角形的各边的长，难度不大．
确定“帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长，然后利用相似三角形的对应边的比相等确定第三个顶点的位置即可．
【解答】
解：帅”、“相”、“兵”所在位置的格点构成的三角形的三边的长分别为2、25、42；
“车”、“炮”之间的距离为1，
“炮”②之间的距离为5，“车”②之间的距离为22，
∵525=2242=12，
∴马应该落在②的位置，
故选：B．
11.【答案】D
【解析】解：∵a4=b3，
∴ab=43，
∴a−bb=ab−1=43−1=13．
故选：D．
根据a4=b3得出ab=43，再把要求的式子化成ab−1，然后进行计算即可得出答案．
此题考查了比例的性质，熟练掌握两内项之积等于两外项之积是解题的关键．
12.【答案】C
【解析】解：过点G作GN⊥AD于N，延长NG交BC于M，
∵四边形ABCD是矩形，
∴AD=BC，AD//BC，
∵EF=12AD，
∴EF=12BC，
∵AD//BC，NG⊥AD，
∴△EFG∽△CBG，GM⊥BC，
∴GN：GM=EF：BC=1：2，
又∵MN=AB=6，
∴GN=2，GM=4，
∴S△BCG=12×10×4=20，
∴S△EFG=12×5×2=5，S矩形ABCD=6×10=60，
∴S阴影=60−20−5=35．
故选：C．
过点G作GN⊥AD于N，延长NG交BC于M，通过证明△EFG∽△CBG，可得GN：GM=EF：BC=1：2，可求GN，GM的长，由面积的和差关系可求解．
本题主要考查了矩形的性质以及相似三角形的判定与性质，求出阴影部分的面积可以转化为几个规则图形的面积的和或差的关系．
13.【答案】5−1
【解析】解：∵点C是线段AB的黄金分割点，且AB=2(AC>BC)，
∴AC=5−12AB=5−12×2=5−1，
故答案为：5−1．
把线段AB分成两条线段AC和BC(AC>BC)，且使AC是AB和BC的比例中项，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．根据黄金分割的定义得到AC=5−12AB，然后把AB的长代入计算即可．
本题考查了黄金分割：把线段AB分成两条线段AC和BC(AC>BC)，且使AC是AB和BC的比例中项(即AB：AC=AC：BC)，叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．特别要注意线段AB的黄金分割点有两个．
14.【答案】102
【解析】解：∵3a=4b，
∴a=34b，
则2a+bb=32b+bb=52=102，
故答案为：102．
根据比例的性质得到a=34b，代入代数式计算即可．
本题考查的是比例的性质，掌握比例的基本性质是解题的关键．
15.【答案】3
【解析】解：由题意知：AB//CD，
则∠BAE=∠C，∠B=∠CDE，
∴△ABE∽△CDE，
∴ABCD=AECE，
∴1CD=0.41.6−0.4，
∴CD=3米，
故答案为：3．
由题意知：△ABE∽△CDE，得出对应边成比例即可得出CD．
本题考查了相似三角形的判定与性质，根据题意得出△ABE∽△CDE是解决问题的关键．
16.【答案】4.5
【解析】解：由题意得：
∠APB=∠CPD，
∵AB⊥BD，CD⊥BD，
∴∠ABD=∠CDB=90°，
∴△ABP∽△CDP，
∴ABCD=BPDP，
∴1.5CD=26，
∴CD=4.5，
∴该古城墙的高度CD是4.5m，
故答案为：4.5．
根据题意可得∠APB=∠CPD，根据垂直定义可得∠ABD=∠CDB=90°，从而可证△ABP∽△CDP，然后利用相似三角形的性质，进行计算即可解答．
本题考查了相似三角形的应用，熟练掌握相似三角形的判定与性质是解题的关键．
17.【答案】解：∵k=a−2bc=b−2ca=c−2ab，且a+b+c≠0，
∴k=a−2b+b−2c+c−2aa+b+c=−a−b−ca+b+c=−(a+b+c)a+b+c=−1．
【解析】根据比例的性质，即可解答．
本题考查了比例的性质，解决本题的关键是熟记比例的性质．
18.【答案】(1)证明：∵BD=2AD，AE=2EC，
∴BDAD=AECE，
∵DF//AC，
∴BDAD=BFCF，
∴BFCF=AECE，
∴EF//AB，
又∵DF//AC，
∴四边形ADFE是平行四边形，
∵AB=2AC，AE=23AC，
∴AE=13AB，
∴AD=AE，
∵四边形ADFE是平行四边形，
∴四边形ADFE是菱形；
(2)如图，在△ADE和△ACB中，∠A是公共角，
ADAC=13ABAC=23ACAC=23，AEAB=23ACAB=23AC2AC=23，
∴△ADE∽△ACB，
∵BC=1，
∴DE=23．
【解析】(1)根据菱形的判定方法解答即可；
(2)根据相似三角形的判定和性质解答即可．
本题主要考查了菱形的判定和相似三角形的判定和性质，熟练掌握这些判定定理和性质定理是解答本题的关键．
19.【答案】解：(1)∵ABAC=AEAD=BECD．
∴△ABE∽△ACD，
∴∠DAE=∠BAE=22°，
∴∠BAD=44°；
(2)△ADE∽△ACB，理由如下：
∵ABAC=AEAD，
∴ABAE=ACAD，
又∵∠DAC=∠BAE，
∴△ADE∽△ACB．
【解析】(1)通过证明△ABE∽△ACD，可得∠DAE=∠BAE=22°，即可求解；
(2)由两组对应边的比相等且夹角对应相等的两个三角形相似，可证明△ADE∽△ACB．
本题考查了相似三角形的判定，掌握相似三角形的判定方法是解题的关键．
20.【答案】解：(1)如图：作出∠APD=∠ABP，即可得到△PCD∽△ABP；
(2)证明：如图，∵∠APC=2∠ABC，∠APD=∠ABC，
∴∠DPC=∠ABC，
∴PD//AB．
【解析】本题考查了尺规作图−作一个角等于已知角，相似三角形的判定等，熟练掌握尺规作图的方法和相似三角形的判定定理是解题的关键．
(1)尺规作图作出∠APD=∠ABP，即可得到∠DPC=∠PAB，从而得到△PCD∽△ABP；
(2)根据题意得到∠DPC=∠ABC，根据平行线的的判定定理即可证得结论．
21.【答案】(1)证明：∵△ABE是等边三角形，
∴AE=AB，
∵四边形ABCD是正方形，
∴AB=BE=AD=CD，∠BAD=∠ADC=90°，
∵OD=CD，
∴OD=AE，
∵EF⊥AB，AB//CD，
∴EF⊥CD，
∴四边形ADGF为矩形，
∴AF=DG，AD=FG，
在Rt△AFE和Rt△DGO中，
AE=ODAF=DG，
∴Rt△AFE≌Rt△DGO(HL)，
∴EF=OG，
∴OE=FG，
∴AD=OE，
又∵AD//OE，
∴四边形ADOE为平行四边形，
∴AE//DO；
(2)证明：∵四边形ADOE为平行四边形，AD=OD=CD，
∴四边形ADOE为菱形，
∴AO⊥ED，
∴∠AMD=90°，
又∵∠EFQ=90°，
∴∠AMD=∠EFQ，
又∵AD//EF，
∴∠ADM=∠QEF，
∴△QEF∽△ADM，
∴EQAD=EFDM．
【解析】(1)由等边三角形的性质及正方形的性质证出OD=AE，证明Rt△AFE≌Rt△DGO(HL)，由全等三角形的性质得出EF=OG，由平行四边形的判定可证出四边形ADOE为平行四边形，由平行四边形的性质可得出结论；
(2)证明四边形ADOE为菱形，由菱形的性质得出AO⊥ED，证明△QEF∽△ADM，由相似三角形的性质可得出结论．
本题考查了平行四边形的判定与性质，正方形的性质，等边三角形的性质，菱形的判定与性质，全等三角形的判定与性质，相似三角形的判定与性质，熟练掌握平行四边形的判定与性质是解题的关键．
22.【答案】证明：(1)∵DE=DC，AD=FD，∠EDF=∠CDA=90°，
∴△CDA≌△EDF(SAS)，
∴∠AEG=∠ACD，
∵∠ACD+∠DAC=90°，
∴∠AEG+∠DAC=90°，
∴∠AGE=90°，
∴AC⊥BE．
(2)在矩形ABCD中，BC//AD，∴BC//DE，
∴△BCF∽△EDF，
∴CFDF=BCDE，
∵BC=AD，DE=CD，
∴CFDF=ADCD，
由(1)得∠AGE=90°=∠CDA，∠AEG=∠ACD，
∴△CDA∽△EAB，
∴ACBE=ADAB，
∵AB=CD，
∴ACBE=ADCD，
∴CFDF=ACBE．
【解析】(1)先证明△CDA≌△EDF，可得∠AEG=∠ACD，从而证得AC⊥BE；
(2)先证明△BCF∽△EDF，可得CFDF=BCDE=ADCD，再由△CDA∽△EAB，可得ACBE=ADAB=ADCD，从而得证．
本题考查了三角形相似的判定及全等的证明，由多组边相等想到证全等是证明题的常见思路，同时第一问的结论往往会衔接到第二问，所以在证第二问时要联系到第一问，这样子思路才会更顺畅！利用已知条件结合相似判定方法是本题解题的关键．
23.【答案】解：(1)如图，△A1B1C1为所作；
(2)如图，△A2B2C2为所作，点B2的坐标为(−4,−6)；

【解析】(1)根据关于y轴对称的点的坐标得到A1、B1、C1的坐标，然后描点即可；
(2)把A、B、C的坐标都乘以−2得到A2、B2、C2的坐标，然后描点即可．
本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或−k.也考查了轴对称变换．
24.【答案】解：由题意知∠CED=∠AEB，∠CDE=∠ABE=90°，
∴△CED∽△AEB．
∴CDDE=ABBE，
∴，
∴AB=35米．
故塔的高度AB为35米．
【解析】如图容易知道CD⊥BD，AB⊥BE，即∠CDE=∠ABE=90°.由光的反射原理可知∠CED=∠AEB，这样可以得到△CED∽△AEB，然后利用对应边成比例就可以求出AB．
考查了相似三角形的应用，本题只要是把实际问题抽象到相似三角形中，利用相似三角形的性质就可以求出结果．
25.【答案】解：由题意得：△CDE∽△ABE，
∴CDAB=DEBE，
∵CD=1.6米，DE=2米，BE=8米，
即：1.6AB=28，
解得：AB=6.4，
答：树高大约是6.4米．
【解析】根据题意得：△CDE∽△ABE，然后利用相似三角形的性质列式计算即可．
考查了相似三角形的应用，解题的关键是从实际问题中抽象出相似三角形，难度不大．