









- 2.3.4《两条平行直线间的距离》课件+教案 课件 74 次下载
- 2.4.1《圆的标准方程》课件+教案 课件 81 次下载
- 2.5.1《直线与圆的位置关系》课件+教案 课件 80 次下载
- 2.5.2《圆与圆的位置关系》课件+教案 课件 79 次下载
- 3.1.1《椭圆及其标准方程(一)》课件+教案 课件 79 次下载
人教A版 (2019)选择性必修 第一册2.4 圆的方程完美版ppt课件
展开人教A版2019高中数学选修一
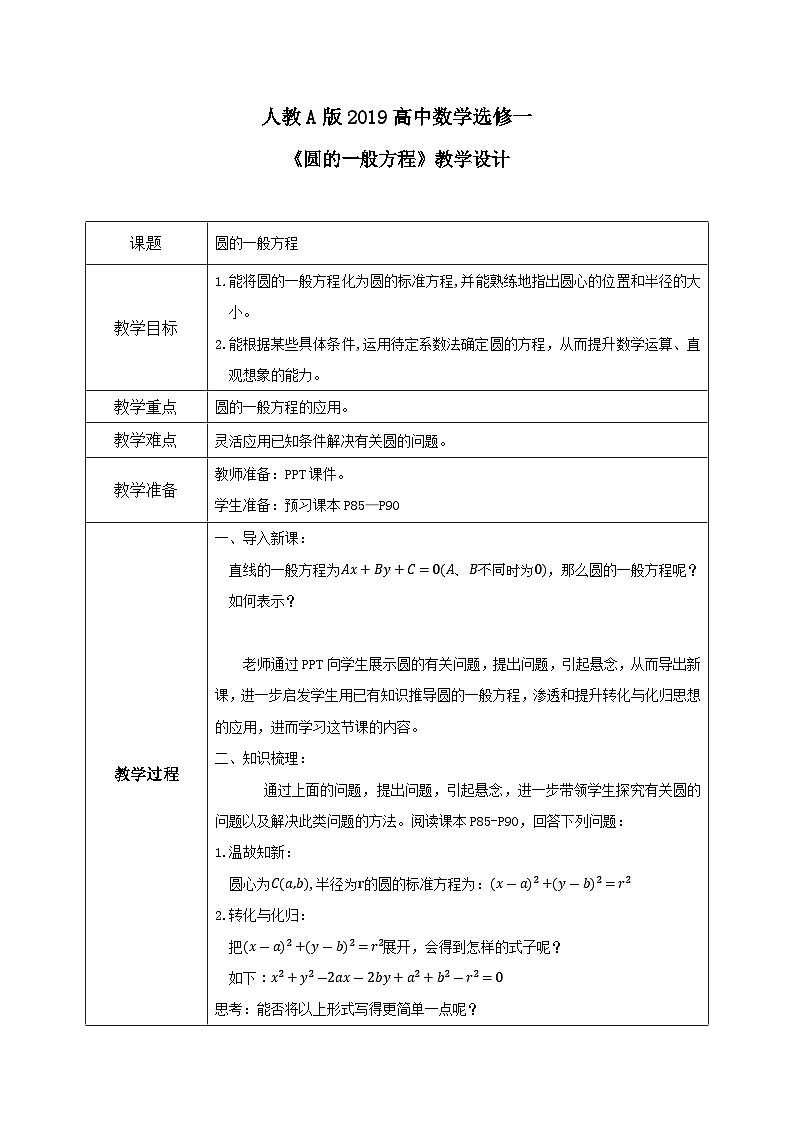
《圆的一般方程》教学设计
课题 | 圆的一般方程 |
教学目标 | 1.能将圆的一般方程化为圆的标准方程,并能熟练地指出圆心的位置和半径的大小。 2.能根据某些具体条件,运用待定系数法确定圆的方程,从而提升数学运算、直观想象的能力。 |
教学重点 | 圆的一般方程的应用。 |
教学难点 | 灵活应用已知条件解决有关圆的问题。 |
教学准备 | 教师准备:PPT课件。 学生准备:预习课本P85—P90 |
教学过程 | 一、导入新课: 直线的一般方程为,那么圆的一般方程呢?如何表示?
老师通过PPT向学生展示圆的有关问题,提出问题,引起悬念,从而导出新课,进一步启发学生用已有知识推导圆的一般方程,渗透和提升转化与化归思想的应用,进而学习这节课的内容。 二、知识梳理: 通过上面的问题,提出问题,引起悬念,进一步带领学生探究有关圆的问题以及解决此类问题的方法。阅读课本P85-P90,回答下列问题: 1.温故知新: 圆心为,半径的圆的标准方程为: 2.转化与化归: 把展开,会得到怎样的式子呢? 如下 思考:能否将以上形式写得更简单一点呢? 由于均为常数,故令
任何一个圆的方程都可以写成下面形式:x2 +y 2+Dx+Ey+F=0 反过来,是不是任何一个形如x2 +y 2+Dx+Ey+F=0 的方程表示的曲线都是圆呢? 辨析:上式配方可得: 讨论:(1)当时,图形表示以心,为半径的圆 (2)当时,方程只有一组解 , 故图形表示一个点 (3)当时,方程无实数解,所以它不表示任何图形. 3.圆的一般方程: 方程,当时,表示以 圆心,为半径的圆,此时叫做圆的一般方程. 方程特点:(1)与系数相同并且不等于0; (2)没有这样的二次项. 4.圆的标准方程与一般方程的对比: 圆的标准方程: 圆的一般方程: () 联系 方程的优点:标准方程易于看出圆心与半径; 一般方程突出形式上的特点
学以致用是每个人必备的思维模型,特别是学生,更要会化解知识体系,故请看下面的练习。 三、跟踪练习: 概念辨析: 1.判断下列方程分别表示什么图形? x2+y2-2x+4y+1=0 x2+y2-2x-4y+5=0 x2+y2-2x-4y+6=0 解表示以 (1,-2) 为圆心, 2为半径的圆. (2) 表示点 (3) 不表示任何图形. 2.已知圆 x2+y2+Dx+Ey+F=0的圆心坐标为 半径为,则分别等于( ) (1) 4,-6,3 (2) -4,6,3 (3) -4,6,-3 (4) 4,-6,-3 答案:(4) 3x2+y2-2ax-y+a=0 圆的方程的条件是( ) ( 提示:方程可化为: 即 答案:D
拓展和提升本节课的数学知识和思维方法是数学学习中必不可少的一个重要环节,请学习下一个环节。 四、课堂互动: 互动一: 1.以下直线中将圆4平分的是( )
提示:圆的标准方程是 坐标是 答案:A 互动二: 2.求过三点的圆的方程. 思维提示: (1)待定系数法---思维简单,基本计算; (2)几何法---数形结合,思维复杂. 解法一:待定系数法 设所求圆的方程为: 都在圆上 解之,得 所求圆的方程为: 互动三: 3.以点为直径端点的圆的方程为( )
. . 思维提示:以点为直径端点的圆的方程 为 0 答案:A 互动四: 4.已知线段的端点的坐标是端点在圆(x+1)2+y2=4上运动, 求线段的中点的轨迹.
解:设点且是线段的中点 则
即=1
数学核心素养价值观的形成是当今数学课改中必不可少的,请回答下列问题 五、素养形成 1.已知圆的方程为,则实数的取值范围是( )
提示:圆的标准方程为 即 答案:C 2.若圆的方程为0,则圆心坐标为( )
提示:由已知得圆的直径两端点的坐标为 即为圆心 答案:D
及时总结,归纳概括,是学习中必须学会的思维模式,进一步提升和拓展,请看: 六、课堂总结: 1.知识小结:(1)方程x2+y2+Dx+Ey+F=0,当D2+E2-4F>0时, 表示以圆心,为半径的圆, 此时叫做圆的一般方程. (2)以点为直径端点的圆的方程为 0 2.解题技巧: (1)灵活应用已知条件求圆的一般方程,标准方程; (2)待定系数法,数形结合思想,转化与化归思想的综合应用. |
课后作业 | 课本P88: 习题2.4 1、2、3、4、5、6、7、8. |
板书设计 |
跟踪练习:1. 4. 2 素养训练:1.. 3. 2. 课堂互动:1. |
教学反思 | 1.要正确灵活的应用已知条件解决有关圆的数学问题。 2.数形结合思想要加强训练。 3.转化与化归思想的渗透与应用。 |
高中数学人教A版 (2019)选择性必修 第一册2.4 圆的方程教课内容课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第一册2.4 圆的方程教课内容课件ppt,共30页。
高中数学人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程多媒体教学课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程多媒体教学课件ppt,共26页。
人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程精品ppt课件: 这是一份人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.4 圆的方程精品ppt课件,共19页。PPT课件主要包含了学习目标,新知学习,典例剖析,相关点法,课堂小结等内容,欢迎下载使用。














