高考数学二轮复习热点突破专题2数列规范答题示范课_数列解答题课件

这是一份高考数学二轮复习热点突破专题2数列规范答题示范课_数列解答题课件，共9页。
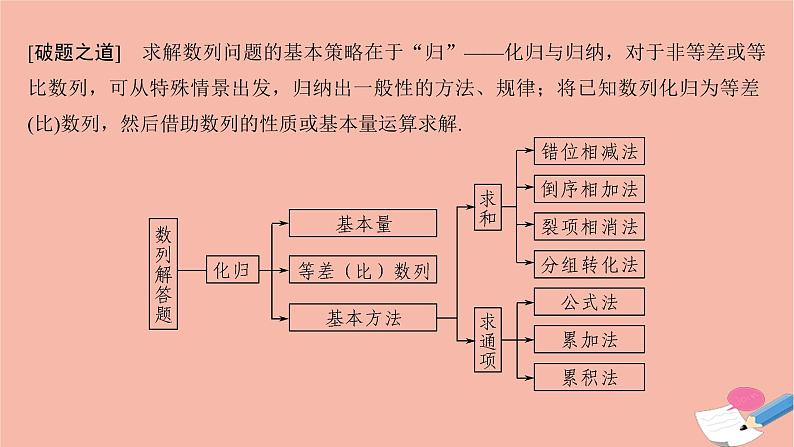
[破题之道]　求解数列问题的基本策略在于“归”——化归与归纳，对于非等差或等比数列，可从特殊情景出发，归纳出一般性的方法、规律；将已知数列化归为等差(比)数列，然后借助数列的性质或基本量运算求解.
(1)求b1，b2，b3；(2)判断数列{bn}是否为等比数列，并说明理由；(3)求{an}的通项公式.
[高考状元满分心得]❶写全得分步骤，踩点得分：对于解题过程中踩分点的步骤有则给分，无则没分，如第(1)问中，写出bn＋1＝2bn，由条件a1＝1，分别求出b1，b2，b3.❷写明得分关键：数列解答题要严谨，如第(2)问“首先明确指出数列{bn}的首项和公比(基本量)，再写出bn＝2n－1.❸计算正确是得分的保证：如第(1)问正确求得b1，b2，b3；第(3)问准确求出an＝n·2n－1，否则不能得分.
[满分体验]1.(2020·全国Ⅲ卷)设等比数列{an}满足a1＋a2＝4，a3－a1＝8.
(1)求{an}的通项公式；(2)记Sn为数列{lg3an}的前n项和.若Sm＋Sm＋1＝Sm＋3，求m.解　(1)设{an}的公比为q，则an＝a1qn－1.
所以{an}的通项公式为an＝3n－1.
由Sm＋Sm＋1＝Sm＋3得m(m－1)＋(m＋1)m＝(m＋3)(m＋2)，即m2－5m－6＝0.解得m＝－1(舍去)或m＝6.