






高考数学二轮复习热点突破专题4概率与统计规范答题示范课_概率与统计解答题课件
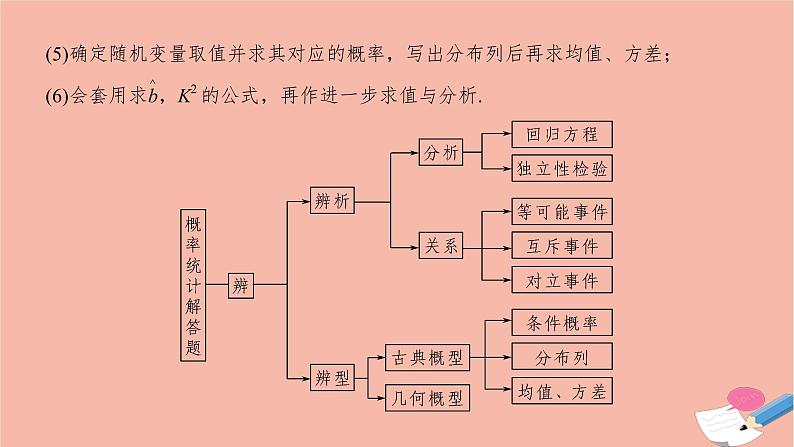
展开[破题之道] 概率与统计问题需要从数据中获取有用的信息,通过数据的筛选、分析构建相关模型特别是从图表、直方图、茎叶图中获取信息,利用图表信息进行数据分析.解题的关键是“辨”——辨析、辨型,求解要抓住几点:(1)准确弄清问题所涉及的事件有什么特点,事件之间有什么关系,如互斥、对立、独立等;(2)理清事件以什么形式发生,如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;(3)明确抽取方式,是放回还是不放回、抽取有无顺序等;(4)准确选择排列组合的方法来计算基本事件发生数和事件总数,或根据概率计算公式和性质来计算事件的概率;
【典例示范】 (12分)(2019·全国Ⅰ卷)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列.(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;②求p4,并根据p4的值解释这种试验方案的合理性.
规范解答 (1)X的所有可能取值为-1,0,1.1分P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β),3分所以X的分布列为
(2)①证明 由(1)得a=0.4,b=0.5,c=0.1,因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),则pi+1-pi=4(pi-pi-1).6分又因为p1-p0=p1≠0,所以{pi+1-pi}(i=0,1,2,…,7)是公比为4,首项为p1的等比数列.8分
[高考状元满分心得]❶写全得分步骤:对于解题过程中是得分点的步骤,有则给分,无则没分,所以对于得分点步骤一定要写全.如第(1)问中,写出随机变量X的可能取值,第(2)问中说明{pi+1-pi}的公比,首项,利用p4的值说明最后的结论合理性等.❷写明得分关键:对于解题过程中的关键点,有则给分,无则没分,所以在答题时一定要写清得分关键点,如第(1)问分布列必须用表格表示,第(2)问中pi+1-pi=4(pi-pi-1)的关系式及条件p1-p0=p1≠0,否则都会导致扣分.❸正确计算是得满分的关键:如第(2)问中累加求p8与p1的关系,由p8求p1,p4的值,若出错,会每次扣去1分.
[满分体验]1.(2020·西安模拟)某生物研究小组准备探究某地区蜻蜓的翼长分布规律,据统计该地区蜻蜓有A,B两种,且这两种的个体数量大致相等.记A种蜻蜓和B种蜻蜓的翼长(单位:mm)分别为随机变量X,Y,其中X服从正态分布N(45,25),Y服从正态分布N(55,25).
(3)在(2)的条件下,从该地区的蜻蜓中随机捕捉3只,记这3只中翼长在区间[42.2,57.8]的个数为W,求W的分布列及数学期望(分布列写出计算表达式即可).注:若X~N(μ,σ2),则P(μ-0.64σ≤X≤μ+0.64σ)≈0.477 3,P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 6.解 (1)记这只蜻蜓的翼长为t.因为A种蜻蜓和B种蜻蜓的个体数量大致相等,所以这只蜻蜓是A种还是B种的可能性是相等的.
(2)由于两种蜻蜓的个体数量相等,X,Y的方差也相等,
(3)设蜻蜓的翼长为T,则P(42.2≤T≤57.8)=P(μ-σ≤T≤μ+σ)=0.682 7.
E(W)=3×0.682 7=2.048 1.
2.(2019·北京卷)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
(1)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;(2)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1 000元的人数,求X的分布列和数学期望;(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2 000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2 000元的人数有变化?说明理由.
解 (1)由题意知,样本中仅使用A的学生有18+9+3=30(人),仅使用B的学生有10+14+1=25(人),A,B两种支付方式都不使用的学生有5人,故样本中A,B两种支付方式都使用的学生有100-30-25-5=40(人).
(2)X的所有可能值为0,1,2.记事件C为“从样本仅使用A的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”,事件D为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于1 000元”.
故X的数学期望E(X)=0×0.24+1×0.52+2×0.24=1.(3)记事件E为“从样本仅使用A的学生中随机抽查3人,他们本月的支付金额都大于2 000元”.假设样本仅使用A的学生中,本月支付金额大于2 000元的人数没有变化.
新高考版高考数学二轮复习(新高考版) 第1部分 专题突破 专题5 规范答题5 概率与统计课件PPT: 这是一份新高考版高考数学二轮复习(新高考版) 第1部分 专题突破 专题5 规范答题5 概率与统计课件PPT,共9页。PPT课件主要包含了高考数学二轮复习策略,思路分析等内容,欢迎下载使用。
新高考数学二轮复习专题五规范答题5概率与统计课件: 这是一份新高考数学二轮复习专题五规范答题5概率与统计课件,共7页。PPT课件主要包含了思路分析等内容,欢迎下载使用。
《新高考数学大二轮复习课件》专题五 规范答题5 概率与统计: 这是一份《新高考数学大二轮复习课件》专题五 规范答题5 概率与统计,共9页。PPT课件主要包含了命题分析,步骤要点,规范解答,阅卷细则等内容,欢迎下载使用。












