高考数学二轮复习第2部分7.1统计与统计案例课件

这是一份高考数学二轮复习第2部分7.1统计与统计案例课件，共38页。PPT课件主要包含了-2-，-3-，命题热点一，命题热点二，命题热点三，命题热点四，-4-，-5-，-6-，-7-等内容，欢迎下载使用。

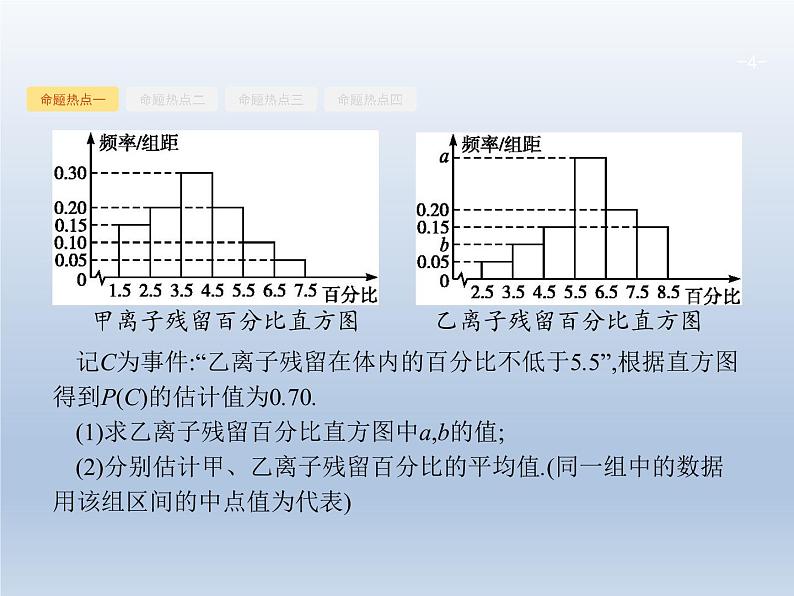
频率分布直方图的应用【思考】 观察频率分布直方图能得到哪些信息?例1为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.(1)求乙离子残留百分比直方图中a,b的值;(2)分别估计甲、乙离子残留百分比的平均值.(同一组中的数据用该组区间的中点值为代表)
解 (1)由已知得0.70=a+0.20+0.15,故a=(2)甲离子残留百分比的平均值的估计值为2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.乙离子残留百分比的平均值的估计值为3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
题后反思利用频率分布直方图求众数、中位数与平均数时,应注意这三者的区分:(1)最高的长方形的中点即众数;(2)中位数左边和右边的直方图的面积是相等的;(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘小长方形底边中点的横坐标之和.
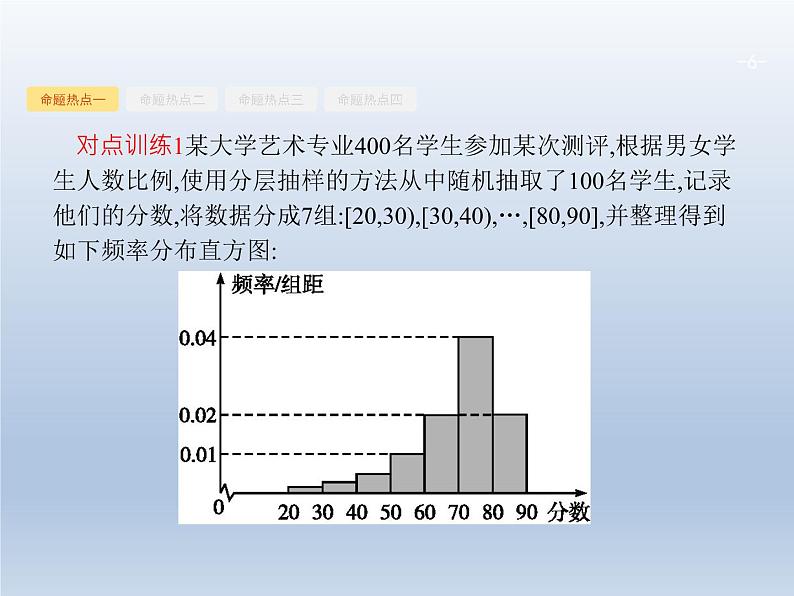
对点训练1某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
解 (1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,所以样本中分数小于70的频率为1-0.6=0.4.所以从总体的400名学生中随机抽取一人,其分数小于70的概率估计为0.4.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,分数在区间[40,50)内的人数为100-100×0.9-5=5.所以总体中分数在区间[40,50)内的人数估计为(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,所以样本中分数不小于70的男生人数为所以样本中的男生人数为30×2=60,女生人数为100-60=40,男生和女生人数的比例为60∶40=3∶2.所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.
用样本的数字特征估计总体【思考1】 样本有哪些数字特征?这些数字特征反映了样本数据的什么情况?【思考2】 茎叶图刻画数据有哪些优点及不足?例2某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
题后反思1.样本的数字特征主要有:中位数、众数、平均数、标准差、方差,中位数、平均数、众数反映了这组数据的集中程度,反映了样本数据的总体水平;而标准差、方差反映这组数据的波动情况,标准差或方差越大,波动越大.2.茎叶图刻画数据的优点:(1)所有数据信息都可由茎叶图看到;(2)茎叶图便于记录和表示,能反映数据在各段上的分布情况.3.茎叶图刻画数据的不足:茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况.
对点训练2某市为了考核甲、乙两部门的工作情况,随机访问了50名市民.根据这50名市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下: (1)分别估计该市的市民对甲、乙两部门评分的中位数;(2)分别估计该市的市民对甲、乙两部门的评分高于90的概率;(3)根据茎叶图分析该市的市民对甲、乙两部门的评价.
解 (1)由所给茎叶图知,50名市民对甲部门的评分由小到大排序,排在第25,26名的是75,75,则样本中位数为75,所以该市的市民对甲部门评分的中位数的估计值是75.
(3)由所给茎叶图知,市民对甲部门的评分的中位数高于对乙部门的评分的中位数,而且由茎叶图可以大致看出对甲部门的评分的标准差要小于对乙部门的评分的标准差,说明该市市民对甲部门的评价较高、评价较为一致,对乙部门的评价较低,评价差异较大.(注:利用其他统计量进行分析,结论合理的也可)
回归方程的求法及回归分析【思考】 两个变量具备什么关系才能用线性回归方程来预测?如何判断两个变量具有这种关系?
例3某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2,…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制的散点图如图所示.
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
题后反思当两个变量之间具有相关关系时,才可通过线性回归方程来估计和预测.对两个变量的相关关系的判断有两个方法:一是根据散点图,具有很强的直观性,直接得出两个变量是正相关或负相关;二是计算相关系数法,这种方法能比较准确地反映相关程度,相关系数的绝对值越接近1,相关性就越强.
对点训练3下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.
(2)利用模型②得到的预测值更可靠.理由如下:(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=-30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型 =99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.
(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.(以上给出了2种理由,答出其中任意一种或其他合理理由均可)
独立性检验【思考】 独立性检验有什么用途?例4某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每名顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
(1)分别估计男、女顾客对该商场服务满意的概率;(2)能否在犯错误的概率不超过5%的前提下认为男、女顾客对该商场服务的评价有差异?
对点训练4海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;(2)填写下面列联表,并根据列联表判断是否在犯错误的概率不超过0.01的前提下认为箱产量与养殖方法有关;
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.附:　
解 (1)旧养殖法的箱产量低于50 kg的频率为(0.012+0.014+0.024+0.034+0.040)×5=0.62.因此,事件A的概率估计值为0.62.(2)根据箱产量的频率分布直方图得列联表
由于15.705>6.635,故在犯错误的概率不超过0.01的前提下认为箱产量与养殖方法有关.
(3)箱产量的频率分布直方图表明:新养殖法的箱产量平均值(或中位数)在50 kg到55 kg之间,旧养殖法的箱产量平均值(或中位数)在45 kg到50 kg之间,且新养殖法的箱产量分布集中程度较旧养殖法的箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法.
1.(2020全国Ⅰ,文5)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10 ℃至40 ℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(　　)A.y=a+bxB.y=a+bx2C.y=a+bexD.y=a+bln x
2.甲、乙两组各5名工人某日的产量数据(单位:件)的茎叶图如图所示.若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为 (　　)A.3,5B.5,5C.3,7D.5,7
解析 甲组数据为56,62,65,70+x,74;乙组数据为59,61,67,60+y,78.若两组数据的中位数相等,则65=60+y,所以y=5.又两组数据的平均值相等,所以56+62+65+70+x+74=59+61+67+65+78,解得x=3.
3.(2020全国Ⅲ,文3)设一组样本数据x1,x2,…,xn的方差为0.01,则数据10x1,10x2,…,10xn的方差为(　　)
4.因为随着科技的发展,近年来看电子书的国人越来越多,所以近期有许多人呼吁“回归纸质书”.目前出版物阅读中纸质书占比出现上升,现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数的 .将这200人按年龄分成五组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65],其中统计看纸质书的人得到的频率分布直方图如图所示.
(1)求a的值及看纸质书的人的平均年龄;(2)按年龄划分,把年龄在[15,45)的称青壮年组,年龄在[45,65]的称为中老年组.若选出的200人中看电子书的中老年人有10人,请完成下面2×2列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
解 (1)由题图可得10×(0.01+0.015+a+0.03+0.01)=1,得a=0.035.所以看纸质书的人的平均年龄为20×10×0.01+30×10×0.015+40×10×0.035+50×10×0.03+60×10×0.01=41.5.