高考数学一轮复习第2章函数导数及其应用第14讲函数模型及其应用课件

这是一份高考数学一轮复习第2章函数导数及其应用第14讲函数模型及其应用课件，共40页。

1.常见的几种函数模型
2.三种函数模型性质比较
1.某家具的标价为132元，若降价以九折出售(即优惠10%)，
仍可获利 10%(相对进货价)，则该家具的进货价是(A.118 元B.105 元C.106 元D.108 元
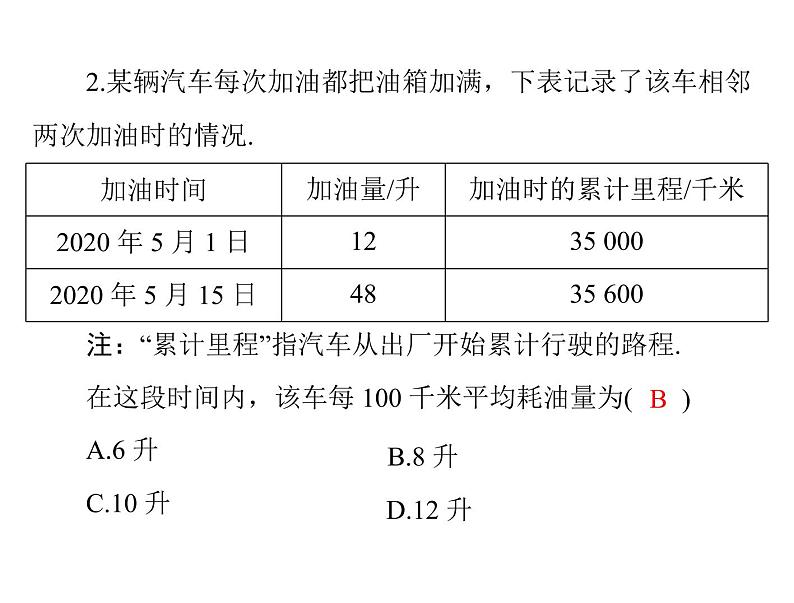
2.某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况.注：“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内，该车每 100 千米平均耗油量为(A.6 升B.8 升C.10 升D.12 升
3.(2018 年黑龙江哈师大附中模拟)某城市出租车起步价为10 元，最远可租乘 3 km(含 3 km)，以后每 1 km 增加 1.6 元(不足1 km按1 km计费)，则出租车的费用y(元)与行驶的路程 x(km)
之间的函数图象大致为(
解析：出租车起步价为 10 元(最远 3 km 的路程)，即在(0,3]内对应 y 的值为 10，以后每 1 km 增加 1.6 元，故选 C.
4.在某种新型材料的研制中，实验人员获得了下列一组实验数据.现准备用下列四个函数中的一个近似地表示这些数据
的规律，其中最接近的一个是(
解析：方法一，由表格知当 x＝3 时，y＝1.59，而 A 中 y
要求；D 中，当 x＝3 时，y＝2.61cs 3<0，不合要求.故选 B.方法二，在平面直角坐标系中描出(x，y)所对应的各点(如图 D17)，由图可知选 B.图 D17
考点 1 正比例、反比例和一次函数类的实际问题例 1：(1)(2017 年河北石家庄模拟)某种新药服用 x 小时后血液中的残留量为 y 毫克，图2-14-1 所示为函数 y＝f(x)的图象，当血液中药物残留量不小于 240 毫克时，治疗有效.设某人上午 8:00 第一次服药，为保证
疗效，则第二次服药最迟的时间应为(
A.上午 10:00C.下午 4:00
B.中午 12:00D.下午 6:00
(2)(2017 年湖北荆州沙市中学统测)成都市某物流公司为了配合“北改”项目顺利进行，决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费 y1 与仓库到车站的距离成反比，而每月车载货物的运费 y2 与仓库到车站的距离成正比.据测算，如果在距离车站 10 千米处建仓库，这两项费用 y1，y2 分别是 2 万元和 8 万元，那么要使这两项费用之和最
小，仓库应建在离车站(A.5 千米处C.3 千米处
B.4 千米处D.2 千米处
解析：设仓库应建在离车站 x 千米处.由仓库每月占用费 y1 与仓库到车站的距离成反比，
∴仓库应建在离车站 5 千米处，可使这两项费用之和最小，最小为 8 万元.故选 A.
函数的综合题型，解决这类问题首先考虑基本不等式，当基本不等式中等号不成立时要利用函数的单调性求最值，当然也可以利用导数求最值.
例 2：某企业生产 A，B 两种产品，根据市场调查与预测，A 产品的利润与投资成正比，其关系如图 2-14-2(1)；B 产品的利润与投资的算术平方根成正比，其关系如图 2-14-2(2).(利润和投资单位：万元)
(1)分别将 A，B 两种产品的利润表示为投资的函数关系式；(2)已知该企业已筹集到 18 万元资金，并将全部投入 A，B
①若平均投入生产两种产品，可获得多少利润？
②问：如果你是厂长，怎样分配这 18 万元投资，才能使该
企业获得最大利润？其最大利润约为多少万元？
此时 x＝16,18－x＝2.∴当 A，B 两种产品分别投入 2 万元、16 万元时，可使该企业获得最大利润，最大利润为 8.5 万元.
【规律方法】二次函数是我们比较熟悉的函数模型，建立二次函数模型可以求出函数的值域或最值.解决实际中的优化问题时，一定要分析自变量的取值范围.利用配方法求最值时，一定要注意对称轴与给定区间的关系：若对称轴在给定的区间内，可在对称轴处取一最值，在离对称轴较远的端点处取另一最值；若对称轴不在给定的区间内，最值在区间的端点处取得.另外，在实际的问题中，还要考虑自变量为整数的问题.
例 3：某种上市股票在 30 天内每股的交易价格 P(元)、日交易量 Q(万股)与时间 t(天)的对应关系分别如下：[有序数对(t，P)落在图 2-14-3 中的折线上，日交易量 Q(万股)与时间 t(天)的部分数据如下表所示.]图 2-14-3
(1)根据图 2-14-3，写出该种股票每股交易价格 P(元)与时间
t(天)所满足的函数关系式；
(2)根据表中数据确定日交易量 Q(万股)与时间 t(天)的一次
(3)用 y(万元)表示该股票日交易额，写出 y 关于 t 的函数关系式，并求这 30 天中第几天日交易额最大，最大值为多少？(注：各函数关系式都要写出定义域.)
故所求 P 满足的函数关系式为
【规律方法】分段函数主要是每一段自变量变化所遵循的规律不同，可以先将其当作几个问题，将各段的变化规律分别找出来，再将其合到一起，要注意各段自变量的范围，特别是端点值的取舍，构造分段函数时，要力求准确、简洁，做到分段合理、不重不漏.
1.个人每次取得的稿费，定额或定率减除规定费用后的余额为应纳税所得额.每次收入不超过 4000 元的，定额减除费用800 元；每次收入在 4000 元以上的，定率减除 20%的费用.适用20%的比例税率，并按规定对应纳税额减征 30%，计算公式为：①每次收入不超过 4000 元的，应纳税额＝(每次收入额－
800)×20%×(1－30%)；
②每次收入在 4000 元以上的，应纳税额＝每次收入额×
(1－20%)×20%×(1－30%).
已知某人出版一份书稿，共纳税 280 元，则这个人应得稿
解析：由题可知，当纳税 280 元时，代入第一个计算公式中，可得 280＝(每次收入额－800)×20%×(1－30%)，此时每
次收入额为 2800 元，
∵2800<4000，∴满足题意.
而代入到第二个计算公式中，得到
280＝每次收入额×(1－20%)×20%×(1－30%)，此时每次
收入额为 2500 元，
∵2500<4000，∴不满足题意，舍去.
若四月份该家庭使用了 20 m3 的煤气，则其煤气费为(
解析：根据题意可知 f(4)＝C＝4，f(25)＝C＋B(25－A)＝14，
f(35)＝C＋B(35－A)＝19，
⊙指数函数、对数函数模型
例题：(2019 年上海)改革开放40年，我国卫生事业取得巨大成就，卫生总费用增长了数十倍.卫生总费用包括个人现在支出、社会支出、政府支出，下表为 2012 年－2015 年我国卫生费用中个人现金支出、社会支出和政府支出的费用(单位：亿元)和在卫生总费用中的占比.
(数据来源于国家统计年鉴)
(1)指出 2012 年到 2015 年之间我国卫生总费用中个人现金支出占比和社会支出占比的变化趋势；
解：(1)由表格数据可知个人现金支出占比逐渐减少，社会支出占比逐渐增多.
∴当 t≥51 时，我国卫生总费用超过 12 万亿.∴预测我国到 2028 年我国卫生总费用首次超过 12 万亿.
【跟踪训练】3.某食品的保鲜时间 y(单位：时)与储藏温度 x(单位：℃)满足函数关系y＝ekx＋b(e为自然对数的底数，k，b为常数).若该食品在 0 ℃的保鲜时间是 192 小时，在 22 ℃的保鲜时间是 48
小时，则该食品在 33 ℃的保鲜时间是(
A.16 小时C.24 小时
B.20 小时D.21 小时
4.某市生产总值连续两年持续增加.第一年的增长率为 p，第二年的增长率为 q，则该市这两年生产总值的年平均增长率
1.解函数应用问题的步骤(四步八字).
(1)审题：弄清题意，分清条件和结论，理顺数量关系，初
(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用数学知识，建立相应的数学模型，建模时一定要注意定义域；
(3)解模：求解数学模型，得出数学结论；(4)还原：将数学结论还原为实际问题的意义.
以上过程用框图表示如图 2-14-4：