高考数学一轮复习第8章立体几何第3讲点直线平面之间的位置关系课件

这是一份高考数学一轮复习第8章立体几何第3讲点直线平面之间的位置关系课件，共46页。PPT课件主要包含了言”“符号语言”列表，⇒l⊂α，P∈αP∈β，异面直线所成的角，锐角或直角，0°90°，一条直线与l，A平行，B相交，C垂直等内容，欢迎下载使用。

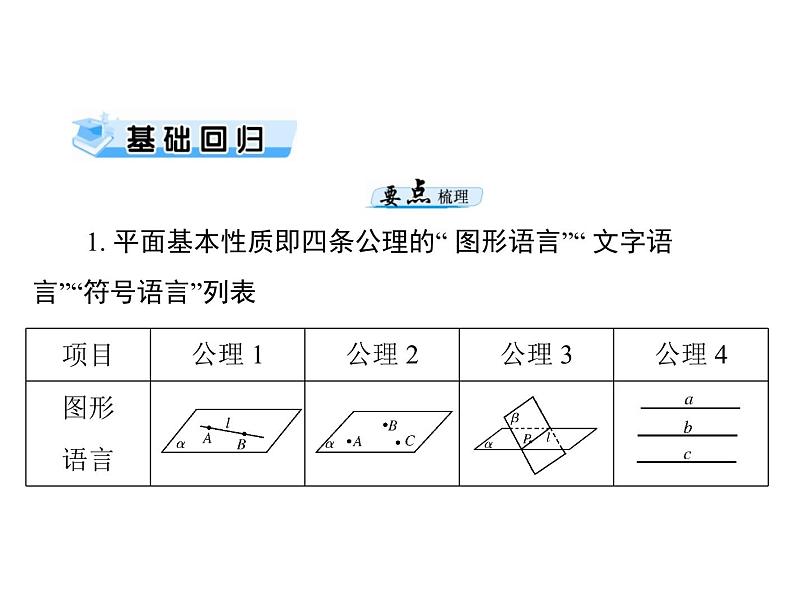
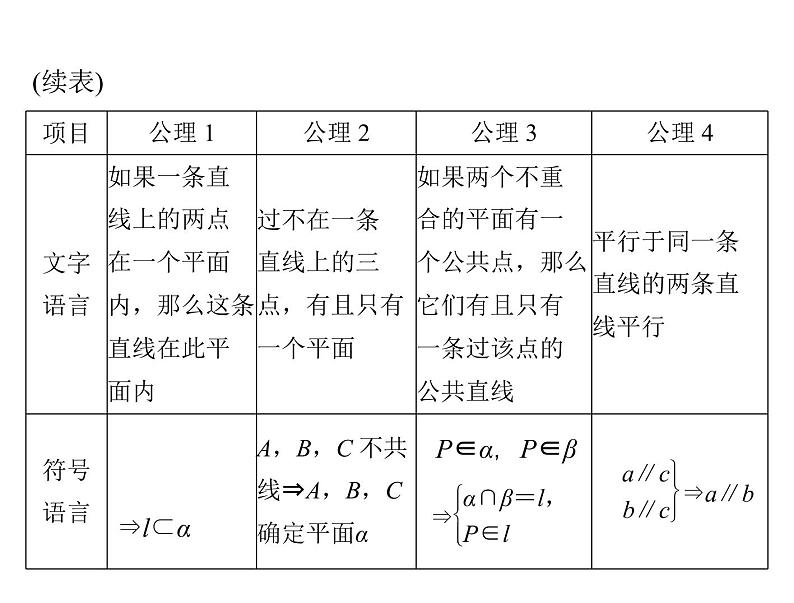
1. 平面基本性质即四条公理的“ 图形语言”“ 文字语
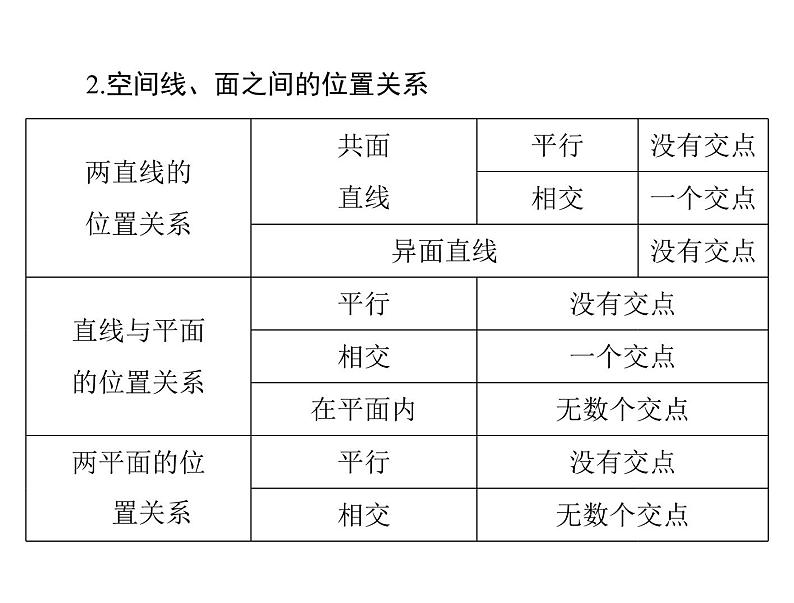
2.空间线、面之间的位置关系
过空间任一点 O 分别作异面直线 a 与 b 的平行线 a′与 b′.那么直线 a′与 b′所成的_______________，叫做异面直线 a与 b 所成的角(或夹角)，其范围是______________.
1.在下列命题中，不是公理的是(
A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点，有且只有一个平面C.如果一条直线上的两点在一个平面内，那么这条直线在此平面内D.如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线
2.(2019 年山西太原期末)已知平面α和直线 l，则α内至少有
解析：直线 l 与平面α斜交时，在平面α内不存在与 l 平行的直线，∴A 错误；l⊂α时，在平面α内不存在与 l 异面的直线，∴D 错误；l∥α时，在平面α内不存在与 l 相交的直线，∴B 错误.无论哪种情形在平面α内都有无数条直线与 l 垂直.故选 C.
3.已知直线 a，b 分别在两个不同的平面α，β内，则“直线
a 和直线 b 相交”是“平面α和平面β相交”的(
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
4.若 A∈α，B∈α，A∈l，B∈l，P∈l，则(
例 1：(1)设 a，b，c 是空间中的三条直线，下面给出四个命题：①若 a∥b，b∥c，则 a∥c；②若 a⊥b，b⊥c，则 a∥c；③若 a 与 b 相交，b 与 c 相交，则 a 与 c 相交；④若 a⊂平面α，b⊂平面β，则 a，b 一定是异面直线.上述命题中错误的是________(写出所有错误命题的序号).
解析：由公理 4 知①正确；当 a⊥b，b⊥c 时，a 与 c 可以相交、平行或异面，故②错误；当 a 与 b 相交，b 与 c 相交时，a 与 c 可以相交、平行，也可以异面，故③错误；a⊂α，b⊂β，并不能说明 a 与 b“不同在任何一个平面内”，故④错误.故填②③④.
(2)(2018 年福建厦门模拟)下列四个命题中，真命题的个数
①如果两个平面有三个不在一条直线上的公共点，那么这两个平面重合；②两条直线可以确定一个平面；③空间中，相交于同一点的三条直线在同一平面内；④若 M∈α，M∈β，α∩β＝l，则 M∈l.
解析：对于①来说，过不共线的三点有且只有一个平面，因此①正确；对于②来说，若两直线异面，则不能确定一个平面，因此②不正确；对于③来说，正方体中一个顶点引出的三条棱，不在同一平面内，因此③不正确；由公理，可知④正确.故选 B.
(3)(多选)下列推断中，正确的是(
A.A∈l，A∈α，B∈l，B∈α⇒l⊂αB.A∈α，A∈β，B∈α，B∈β⇒α∩β＝ABC.l⊄ α，A∈l⇒A∉ αD.A，B，C∈α，A，B，C∈β，且 A，B，C 不共线⇒α，β重合答案：ABD
【规律方法】直线在平面内也叫平面经过直线，如果直线不在平面内，记作 l⊄ α，包括直线与平面相交及直线与平面平行两种情形.反映平面基本性质的三个公理是研究空间图形和研究点、线、面位置关系的基础，三个公理也是立体几何作图和逻辑推理的依据.公理 1 是判断直线在平面内的依据；公理 2的作用是确定平面，这是把立体几何转化成平面几何的依据；公理 3 是证明三(多)点共线或三线共点的依据.
空间内两直线的位置关系
例 2：(1)在正方体 ABCD-A1B1C1D1 中，E，F 分别是线段
BC，CD1 的中点，则直线 A1B 与直线 EF 的位置关系是(
解析：如图 D74 所示，直线 A1B 与直线外一点 E 确定的平面为 A1BCD1，EF⊂平面 A1BCD1，且两直线不平行，故两直线相交.
(2)如图 8-3-1，正方体 ABCD-A1B1C1D1 中，M，N 分别为棱C1D1，C1C 的中点，有以下四个结论：①直线 AM 与 CC1 是相交直线；②直线 AM 与 BN 是平行直线；③直线 BN 与 MB1 是异面直线；
④直线 AM 与 DD1 是异面直线.
其中正确的结论为________(注：把你认为正确的结论序号都填上).
解析：∵点 A 在平面 CDD1C1 外，点 M 在平面 CDD1C1 内，直线 CC1 在平面 CDD1C1 内，CC1 不过点 M，∴AM 与 CC1 是异面直线.故①错；取 DD1 中点 E，连接 AE，则 BN∥AE，但 AE与 AM 相交.故②错；∵B1 与 BN 都在平面 BCC1B1 内，M 在平面 BCC1B1 外，BN 不过点 B1，∴BN 与 MB1 是异面直线.故③正确；同理④正确，故填③④.
(3)(2019 年新课标Ⅲ)如图 8-3-2，点 N 为正方形 ABCD 的中心，△ECD 为正三角形，平面 ECD⊥平面 ABCD，M 是线段
图 8-3-2A.BM＝EN，且直线 BM，EN 是相交直线B.BM≠EN，且直线 BM，EN 是相交直线C.BM＝EN，且直线 BM，EN 是异面直线D.BM≠EN，且直线 BM，EN 是异面直线
解析：如图 D75 所示， 作 EO⊥CD 于 O，连接 ON，过 M作 MF⊥OD 于 F，连 BF，∵平面 CDE⊥平面 ABCD，EO⊥CD，EO⊂平面 CDE，∴EO⊥平面 ABCD，MF⊥平面 ABCD，∴△MFB 与△EON 均为直角三角形.
【规律方法】判断直线是否平行比较简单直观，可以利用公理 4；判断直线是否异面则比较困难，掌握异面直线的两种判断方法：①反证法：先假设两条直线不是异面直线，即两条直线平行或相交，再由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设，肯定两条直线异面；②在客观题中，也可用下述结论：过平面外一点和平面内一点的直线，与平面内不过该点的直线是异面直线.
例 3：(1)(2018 年新课标Ⅱ)在正方体 ABCD-A1B1C1D1 中，E 为棱 CC1 的中点，则异面直线 AE 与 CD 所成角的正切值为
图 8-3-3答案：C
(2)(2016 年新课标Ⅰ)平面α过正方体 ABCD-A1B1C1D1 的顶点 A，α∥平面 CB1D1，α∩平面 ABCD＝m，α∩平面 ABB1A1＝
n，则 m，n 所成角的正弦值为(
解析：如图 8-3-4，设平面 CB1D1∩平面 ABCD＝m′，平
面 CB1D1∩平面 ABB1A1＝n′，
∵α∥平面 CB1D1，∴m∥m′，n∥n′.
则 m，n 所成的角等于 m′，n′所成的角.延长 AD，过 D1作 D1E∥B1C，连接 CE，B1D1，则 CE 为 m′.同理 B1F1 为 n′.而 BD∥CE，B1F1∥A1B，则 m′，n′所成的角即为 A1B，BD 所成的角，即为 60°，
【规律方法】(1)求异面直线所成的角常用方法是平移法，平移的方法一般有三种类型：利用图中已有的平行线平移；利用特殊点(线段的端点或中点)作平行线平移；补形平移.(2)求异面直线所成的角的三步曲：即“一作、二证、三求”.其中空间选点任意，但要灵活，经常选择“端点、中点、等分点”，通过作三角形的中位线，平行四边形等进行平移，作出异面直线所成的角，转化为解三角形问题，进而求解.
【跟踪训练】1.已知 P 是△ABC 所在平面外的一点，M，N 分别是 AB，
C.60° D.90°
解析：如图 D76，取 AC 中点 D，连接 DN，DM，图 D76
三点共线、三线共点的证明
例 4：如图 8-3-5，在正方体 ABCD-A1B1C1D1 中，E，F 分别是 AB 和 AA1 的中点.求证：(1)E，C，D1，F 四点共面；(2)CE，D1F，DA 三线共点.图 8-3-5
证明：(1)如图 8-3-6，连接 EF，CD1，A1B.
∵E，F 分别是 AB，AA1 的中点，∴EF∥BA1.又 A1B∥D1C，∴EF∥CD1.∴E，C，D1，F 四点共面.
∴CE 与 D1F 必相交.
设交点为点 P，如图 8-3-6，
则由点 P∈CE，CE⊂平面 ABCD，得点 P∈平面 ABCD.同理点 P∈平面 ADD1A1.
又平面 ABCD∩平面 ADD1A1＝DA，∴点 P∈直线 DA.
∴CE，D1F，DA 三线共点.
【规律方法】证明三线共点的步骤就是先说明两线交于一点，再证明此交点在另一条线上，把三线共点的证明转化为三点共线的证明，要证明 D，A，P 三点共线，由公理 3 知，只要证明 D，A，P 都在两个平面的交线上即可.
证明多点共线问题：①可由两点连一条直线，再验证其他各点均在这条直线上；②可直接验证这些点都在同一条特定的直线上——相交两平面的唯一交线，关键是通过绘出图形，作出两个适当的平面或辅助平面，证明这些点是这两个平面的公共点.
【跟踪训练】2.如图 8-3-7，α∩β＝l，A，B∈α，C∈β，且 C∉ l，直线AB∩l＝M，过 A，B，C 三点的平面记作γ，则γ与β的交线必通
A.点 AC.点 C 但不过点 M
B.点 BD.点 C 和点 M
解析：∵AB⊂γ，M∈AB，∴M∈γ.又α∩β＝l，M∈l，∴M∈β.
根据公理 3 可知，M 在γ与β的交线上.同理可知，点 C 也在
γ与β的交线上.故选 D.
3.如图 8-3-8，ABCD-A1B1C1D1 是长方体，O 是 B1D1 的中点，
直线 A1C 交平面 AB1D1 于点 M，则下列结论正确的是(图 8-3-8A.A，M，O 三点共线B.A，M，O，A1 不共面C.A，M，C，O 不共面D.B，B1，O，M 共面
解析：(1)连接 A1C1，AC，则 A1C1∥AC，
∴A1，C1，A，C 四点共面，∴A1C⊂平面 ACC1A1，∵M∈A1C，∴M∈平面 ACC1A1.
又 M∈平面 AB1D1，∴M 在平面 ACC1A1 与平面 AB1D1 的交
同理 O 在平面 ACC1A1 与平面 AB1D1 的交线上.∴A，M，O 三点共线.答案：A
难点突破⊙空间中的线面关系例题：(2018 年新课标Ⅰ)已知正方体的棱长为 1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积
图 8-3-9答案：A
【跟踪训练】4.(2019 年上海)已知平面α，β，γ两两垂直，直线 a，b，c满足：a⊂α，b⊂β，c⊂γ，则直线 a，b，c 不可能满足以下哪
A.两两垂直C.两两相交
B.两两平行D.两两异面
解析：如图 D77(1)，可得 a，b，c 可能两两垂直；如图 D77(2)，可得 a，b，c 可能两两相交；如图 D77(3)，可得 a，b，c 可能两两异面.故选：B.
1. 反映平面基本性质的三个公理是研究空间图形和研究点、线、面位置关系的基础，三个公理也是立体几何作图和逻辑推理的依据.公理 1 是判断直线在平面内的依据； 公理 2 的作用是确定平面，这是把立体几何转化成平面几何的依据；公理 3 是证明三(多)点共线或三线共点的依据.
2.正确理解异面直线“不同在任何一个平面内”的含义，不要理解成“不在同一个平面内”.掌握异面直线的两种判断方法：
(1)反证法：先假设两条直线不是异面直线，即两条直线平行或相交，由假设的条件出发，经过严格的推理，导出矛盾，从而否定假设肯定两条直线异面.
(2)客观题中，也可用下述结论：过平面外一点和平面内一
点的直线，与平面内不过该点的直线是异面直线.