



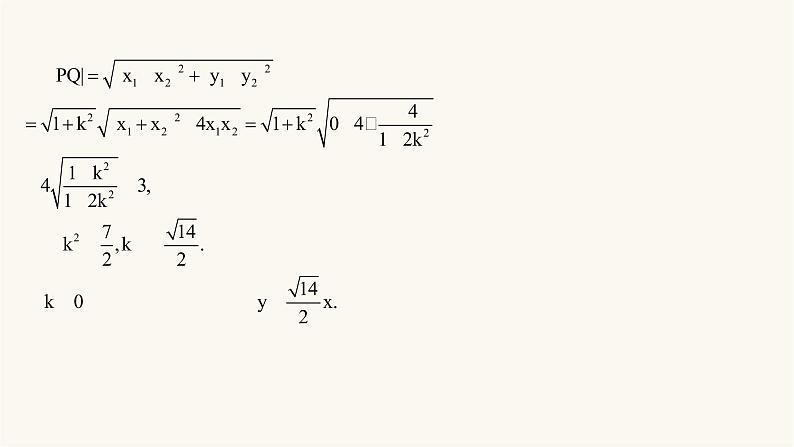

还剩6页未读,
继续阅读
高考数学二轮专题训练高考大题专项练10解析几何b组课件
展开这是一份高考数学二轮专题训练高考大题专项练10解析几何b组课件,共12页。
1.已知椭圆G: =1(a>b>0)的左焦点为F ,且经过点CA,B分别是G的右顶点和上顶点,过原点O的直线l与G交于P,Q两点(点Q在第一象限),且与线段AB交于点M.(1)求椭圆G的标准方程;(2)若 =3,求直线l的方程;(3)若△BOP的面积是△BMQ的面积的4倍,求直线l的方程.
【解析】(1)依题知c= ,则椭圆的右焦点为F1 ( ,0),因为点C 在椭圆上,且|CF1|= =3,又|CF|=1,所以2a=|CF1|+|CF|=4,所以a=2,所以b2=a2-c2=4-2=2,所以椭圆的标准方程为 .
(2)因为点Q在第一象限,所以直线l的斜率存在,设直线l的斜率为k(k>0),则直线l的方程为y=kx,设直线 l与该椭圆的交点为P(x1,y1),Q(x2,y2) ,由 可得(1+2k2)x2-4=0,易知Δ>0,且x1+x2=0,x1x2= ,
(3)设M(xm,ym),Q(x0,y0),则P(-x0,-y0),易知0
【解析】(1)若选①,设P(x,y),根据题意, ,整理得 +y2=1,所以所求的轨迹方程为 +y2=1.若选②,设P(x,y),直线l与圆相切于点H,则|PA|+|PB|=d1+d2=2|OH|=4>2 =|AB|,由椭圆定义知,点P的轨迹是以A,B为焦点的椭圆,所以2a=4,2c=|AB|=2 ,故a=2,c= ,b=1,
所以所求的轨迹方程为 +y2=1.若选③,设P(x,y),S(x′,0),T(0,y′),则 =3(*),因为 ,所以 整理得 代入(*)得 +y2=1,所以所求的轨迹方程为 +y2=1.
(2)设Q(0,y0),当l′斜率不存在时,y0=0,当l′斜率存在时,设直线l′的方程为y=k(x-1)(k≠0),M(x1,y1),N(x2,y2),由 消去y并整理,得(1+4k2)x2-8k2x+4(k2-1)=0,Δ>0恒成立,x1+x2= ,设线段MN的中点为G(x3,y3),则x3= ,y3=k =- ,
相关课件
高考数学二轮专题训练高考大题专项练12解析几何d组课件:
这是一份高考数学二轮专题训练高考大题专项练12解析几何d组课件,共11页。
高考数学二轮专题训练高考大题专项练14函数与导数b组课件:
这是一份高考数学二轮专题训练高考大题专项练14函数与导数b组课件,共9页。
高考数学二轮专题训练高考大题专项练13函数与导数a组课件:
这是一份高考数学二轮专题训练高考大题专项练13函数与导数a组课件,共10页。












