小学数学苏教版六年级上册七 整理与复习背景图ppt课件

这是一份小学数学苏教版六年级上册七 整理与复习背景图ppt课件，共13页。PPT课件主要包含了思路导引，点评苑，完全解答，+13元，+14块，×330元，+30%130%，%-14%等内容，欢迎下载使用。

23.我们班女生有（ ）人，是男生人数的 ；男生有（ ）人，占全班总人数的（ ）%；女生人数是男生人数的（ ）%；女生与男生人数的比是（ ）。
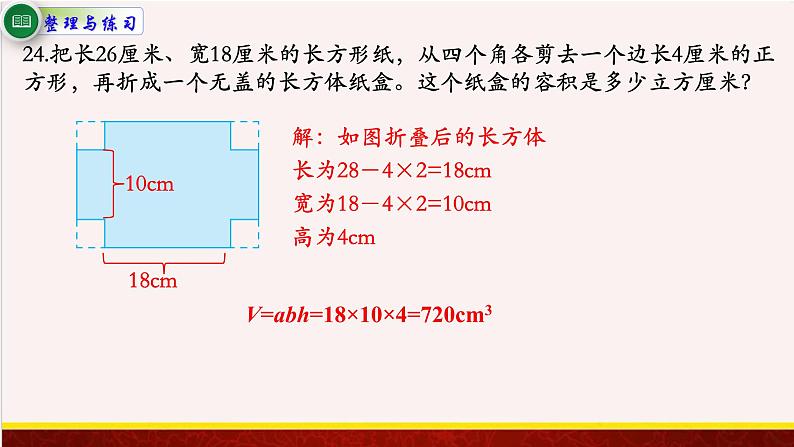
24.把长26厘米、宽18厘米的长方形纸，从四个角各剪去一个边长4厘米的正方形，再折成一个无盖的长方体纸盒。这个纸盒的容积是多少立方厘米？
解：如图折叠后的长方体长为28－4×2=18cm宽为18－4×2=10cm高为4cm
V=abh=18×10×4=720cm3
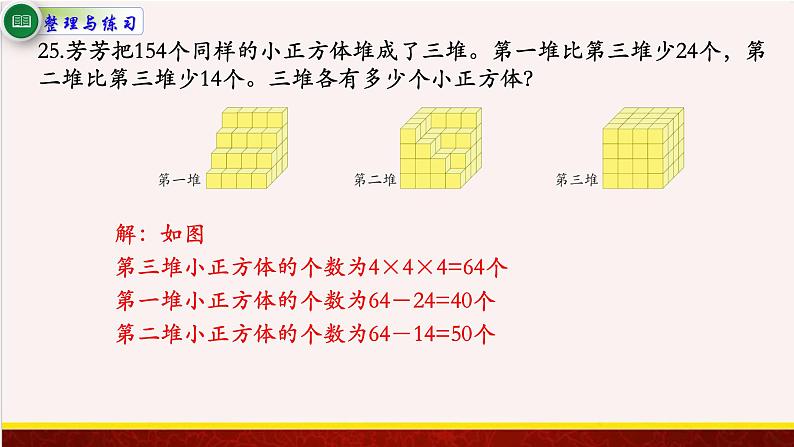
25.芳芳把154个同样的小正方体堆成了三堆。第一堆比第三堆少24个，第二堆比第三堆少14个。三堆各有多少个小正方体？
解：如图第三堆小正方体的个数为4×4×4=64个第一堆小正方体的个数为64－24=40个第二堆小正方体的个数为64－14=50个
典型题型一：用假设的策略解决实际问题
【例题1】学校买来红糖30千克、白糖20千克，每千克白糖比红糖贵1元，共用去120元。每千克红糖和白糖各多少元？
假设买的全是红糖，那么总价要比120元少20×1=20（元），此时共买了50千克红糖，共用去120-20=100（元），可以先求出每个千克红糖的价钱，再求出每千克白糖的价钱。
用假设的策略解决问题时要注意是把什么量替换成什么量，特别要关注题中的数量关系发生了什么变化。
120-20×1=100（元）
100÷（30+20）=2（元）
答：每千克红糖2元，每千克白糖3元.
典型题型二：生活中的极值问题
【例题2】为了绿化城市，某街道要栽种一批树苗，这种树苗的成活率在75%~80%之间。如果栽活1200棵树苗，那么最少栽了多少棵树苗？如果要保证栽活1200棵树苗，那么最多要栽多少棵树苗？
栽活的树苗数=栽的总棵数×成活率。要使树苗栽得最少，那么选这批树苗最高的成活率，所以此时1200棵对应的百分率是80%。要保证栽省籍 1200棵，就要按最成活率最低的情况考虑，所以此时1200棵对应的百分率是75%。
解决百分率中的极值问题时，不是要求最多就找最大的百分率，也不是要求最少就找最小的百分率。要仔细审题，找出对应的百分率，再解决问题。
1200÷80%=1500（棵）
答：如果栽活1200棵树苗，那么最少栽1500棵树苗.
1200÷75%=1600（棵）
答：如果要保证栽活1200棵树苗，那么最多要栽1600棵树苗.
典型题型三：商品销售中的问题
【例题3】一种商品第一次降价10%，第二次又降价20%，要想恢复原价，应在第二次降价的基础上提价几分之几？
“第一次降价10%”是把原价看成单位“1”，而“第二次又降价20%”是把第一次降价后的价格看成单位“1”，后来“要想恢复原价”是把第二次降价之后的价格看成单位“1”。
本题中涉及的三个单位“1”各不相同，这也是本题在解题过程中最容易出错的地方。其实在降价或提价之后，如果再发生变化，那么都是把降价或提价之后的价格看成单位“1”。
（1-10%）×（1-20%）=72%
典型题型四：较复杂的倍数关系的假设
【例题4】小迪买了4盒巧克力和7袋饼干，共用去150元，每盒巧克力的价钱比每袋饼干价钱的4倍还多3元。每盒巧克力和每袋饼干各多少元？
假设每盒巧克力降价3元出售，则买4盒巧克力就能少用去（3×4）元，则买4盒巧克力和7袋饼一共用去（150-3×4）元，且每盒巧克力的价钱正好是每袋饼干的4倍，因此可以把巧克力假设成饼干，1盒巧克力换4袋饼干，那么可以买（4×4+7）袋饼干。先求出饼干的单价，进而求出巧克力的单位。
在用假设法解决复杂问题时，有时需要先根据已知条件进行两次甚至三次假设，再根据其中的数量关系解决问题。
饼干：（150-3×4）÷（4×4+7）=6（元）
巧克力：6×4+3=27（元）
答：每盒巧克力27元，每袋饼干各6元。
典型题型五：购物促销中“买几赠一”问题
【例题5】超市里的香皂每块3元，周末进行促销活动，买三送一，不足三块不赠送。李阿姨买了10块香皂回家，她买这些香皂相当于打了几折？
“买三送一”表示原来买3块香皂的钱促销期间可以买到3+1=4（块）香皂，也就是现在4块香皂为一组，其中有1块不要给钱。现在买10块香皂，先看10里有几个4，就可以少花几个1块香皂的钱，求出现在买10块香皂的钱，再与原来买10块香皂需要的钱比，求出相当于打的折数。
解答“买m送n”，求买a个相当于打几折的问题，是把（m+n)看作一组，再看a里有这样的几组，算出实际买的总价，再除以原来买a个需要的总价，求出实际打的折。
10÷4=2（组）……2（块）
答：她买这些香皂相当于打了八折。
（10-2×1）×3=24（元）
24÷30=80%=八折。
典型题型六：稍复杂的利润问题
【例题6】一种商品按30%的利润率定价，为了提高销量，按定价打八折，结果每件商品仍获利4元。这种商品的成本是多少元？
“按30%的利润率定价”，是把商品的成本看作单位“1”，利润是成本的30%，即定价是成本的1+30%=130%。“按定价打八折”，这时候的定价就是成本的130%×80%=104%，求出此时的利润率，进而求出成本。
与利润相关的实际问题，通常成本是一个不变量，可以将它看作单位“1”。观察题目中其它相关量的变化情况，以数量关系“利润=成本×利润率”作为基本关系，找出其中隐藏的其它数量关系进行解答。
答：这种商品的成本是100元。
130%×80%=104%
4÷4%=100（元）
1.用250克死海的海水能制出75克盐，用250克东海的海水能制出15克盐。死海海水的含盐率是多少？东海呢？
答：死海的含盐率是30%， 东海含盐率是6%。