2021-2022学年福建省莆田市高一（下）期末数学试卷（Word解析版）

这是一份2021-2022学年福建省莆田市高一（下）期末数学试卷（Word解析版），共22页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年福建省莆田市高一（下）期末数学试卷 题号一二三四总分得分       一、单选题（本大题共8小题，共40分）复数其中为虚数单位，则的虚部是(    )A.  B.  C.  D. 若向量，，且，则实数的值为(    )A.  B.  C.  D. 或按从小到大顺序排列的个数据：，，，，，，，，，若这组数据的第一四分位数与第三四分位数的和是，则等于(    )A.  B.  C.  D. 复数的共轭复数是，若复数在复平面内对应的点是，则(    )A.  B.  C.  D. 设，是两条不同的直线，，是两个不同的平面，则下列命题正确的是(    )A. 若，，则
B. 若，，，则
C. 若，，则
D. 若，，，则锐角的三个内角，，所对的边分别是，，，某数学兴趣小组探究该三角形时，提出以下四个论断：甲：；乙：；丙：；丁：若上述四个论断中有且只有一个是正确的，则正确的是(    )A. 甲 B. 乙 C. 丙 D. 丁如图，在平面四边形中，，，则向量在向量上的投影向量为(    )A.
B.
C.
D.
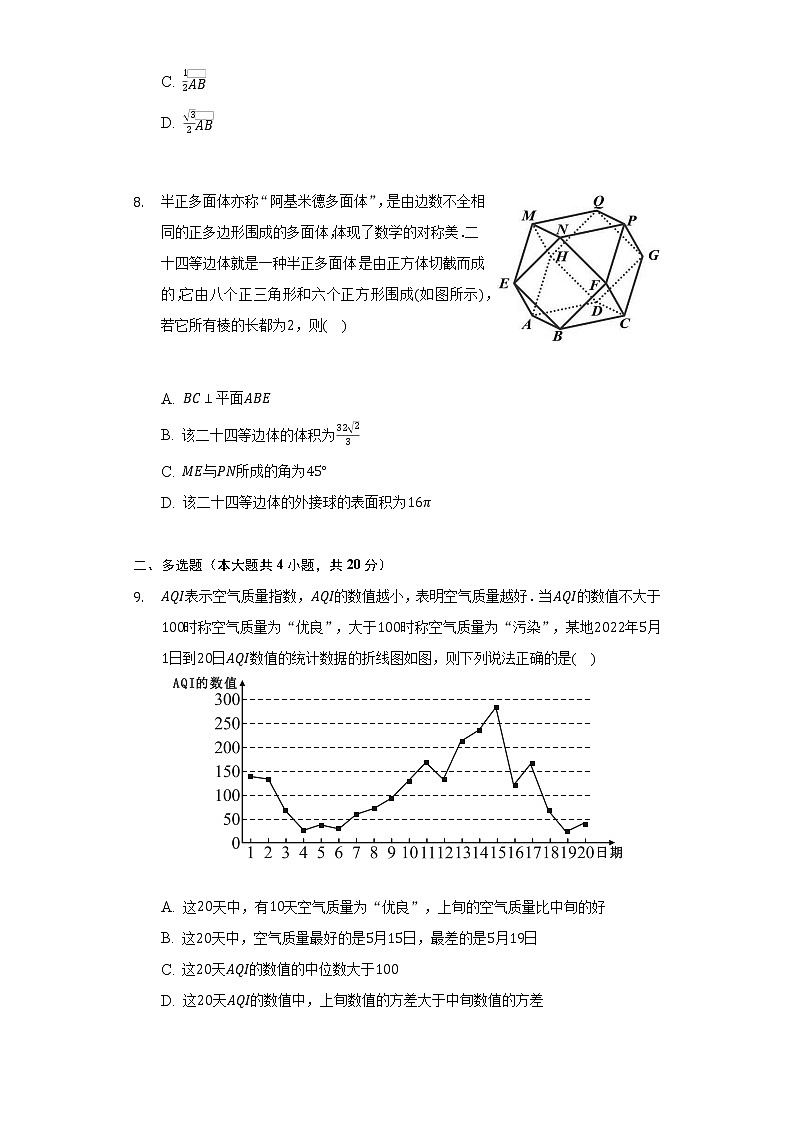
 半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成如图所示，若它所有棱的长都为，则(    )
 A. 平面
B. 该二十四等边体的体积为
C. 与所成的角为
D. 该二十四等边体的外接球的表面积为 二、多选题（本大题共4小题，共20分）表示空气质量指数，的数值越小，表明空气质量越好．当的数值不大于时称空气质量为“优良”，大于时称空气质量为“污染”，某地年月日到日数值的统计数据的折线图如图，则下列说法正确的是(    )
A. 这天中，有天空气质量为“优良”，上旬的空气质量比中旬的好
B. 这天中，空气质量最好的是月日，最差的是月日
C. 这天的数值的中位数大于
D. 这天的数值中，上旬数值的方差大于中旬数值的方差设复数，为虚数单位，是的共轭复数，则下列说法正确的是(    )A. 若，则 B. 若，则
C.  D. 如图，在正方体中，线段上有两个动点，，且为正常数，则下列结论中正确的是(    )A.
B. 线段上存在点，，使得
C. 的面积与的面积之比为
D. 三棱锥的体积为定值
 
 在中，，，是的中点，则下列说法正确的是(    )A. 若，点在线段的延长线上，则
B. 若是的中点，与相交于点，则
C. 若点在线段上，则的值可以是
D. 若是线段上一动点，则为定值 三、填空题（本大题共4小题，共20分）某单位职工分为青年、中年、老年三类，且青年、中年、老年职工的人数之比为：：从中抽取人作为样本，则该单位青年职工被抽取的人数为______人．定义：，两个向量的叉乘的模为，，，表示向量与的夹角．若点，，为坐标原点，则______．已知圆台的轴截面面积为，母线与底面所成的角为，则圆台的侧面积为______．在空间四边形中，，，，二面角的平面角为，为的中点，则与所成的角为______若点为的重心，则______． 四、解答题（本大题共6小题，共70分）已知向量，，
求；
求与的夹角的余弦值．定理证明：请用向量方法证明余弦定理只需证明其中的一个式子即可；
定理应用：如图，在平面四边形中，，，，，求的长．
某市为了解疫情期间本地居民对当地防疫工作的满意度，从本市居民中随机抽取若干人进行满意度测评测评分满分为分根据测评的数据制成频率分布直方图如下：

根据频率分布直方图，回答下列问题：
估计本次测评分数的中位数精确到和平均数同一组中的数据用该组区间的中点值作代表；
估计本次测评分数的第百分位数精确到；
若该市居民约为万人，估计全市居民对当地防疫工作满意度测评分数在分以上的人数．如图，在直三棱柱中，，，为的中点，，，．
证明：平面；
证明：B.
在；；．
这三个条件中任选一个，补充在下面问题中，并解答．
问题：已知，，分别为三个内角，，的对边，，且_____．
求的值；
若，求外接圆的面积．
注：如果选择多个条件分别解答，则按第一个解答计分．如图，在四棱锥中，底面为矩形，是边长为的正三角形，平面平面，为棱的中点．
求证：平面；
若直线与平面所成角的正切值为，求侧面与侧面所成二面角的大小．

答案和解析 1.【答案】 【解析】解：，
则的虚部为．
故选：．
根据已知条件，结合复数的四则运算，以及虚部的定义，即可求解．
本题主要考查复数的四则运算，以及虚部的定义，属于基础题．
 2.【答案】 【解析】解：，，且，
，即，解得或．
故选：．
根据已知条件，结合向量平行的性质，即可求解．
本题主要考查向量平行的性质，属于基础题．
 3.【答案】 【解析】解：由题干可知为个数据．
所以，所以第一四分位数为．
因为，所以第三四分位数为．
则．
所以．
故选：．
先求第一四分位数与第三四分位数，再根据二者之和等于构造方程求解．
本题主要考查四分位数的求法，属于基础题．
 4.【答案】 【解析】解：设，
由得，
即，，
，．
 则
故选：．
根据已知条件，结合共轭复数的定义，以及复数的几何意义，即可求解．
本题主要考查共轭复数的定义，以及复数的几何意义，属于基础题．
 5.【答案】 【解析】解：对于，若，，则或，故A错误；
对于，若，，，则或与异面，即B错误；
对于，若，，由直线与平面垂直的性质可得，故C正确；
对于，若，，，则与的关系为平行、相交或异面，故D错误；
故选：．
，由直线与直线平行、直线与平面平行分析线面关系即可判断；
，若，，，则或与异面；
，由直线与直线平行、直线与平面垂直分析线面关系即可判断；
，由两垂直平面中两直线的位置关系即可判断．
本题考查了命题真假的判断问题，也考查了空间中线线、线面、面面间的位置关系，是基础题．
 6.【答案】 【解析】解：假设甲正确，即，因为，，函数在上单调递减，
所以，即乙也正确，故与题意矛盾，
假设乙正确，即，因为，，函数在上单调递减，
所以，故甲也正确，故与题意矛盾；
假设丙正确，故，由于，故，
因为，，所以，函数在上单调递增，
所以，即，此时，和的大小无法确定，故甲、乙、丁无法确定，故满足题意；
假设丁正确，由，即，即，
即，因为，，所以，
所以，即，故甲也正确，故与题意矛盾．
故选：．
直接利用三角函数关系式的变换，三角函数的值判断命题的真假．
本题考查三角形的正弦定理和两角差公式的运用，考查推理能力，属于基础题．
 7.【答案】 【解析】解：因为，，所以和的夹角为，且
故投影向量为：．
故选：．
根据投影向量的公式直接求解即可．
本题主要考查向量的投影向量，属于基础题．
 8.【答案】 【解析】解：依题意，补齐正方体，如下图，

对于，假设平面，平面，
，，
二十四等边体就是一种半正多面体，
由对称性可知，六边形为正六边形，
，
这与“”矛盾，所以假设不成立，A错误；
对于，，正方体的棱长为，
该二十四等边体的体积为正方体体积去掉个三棱锥体积，
即错误；
对于，，
为异面直线与所成角或补角，
在等边中，，C错误；
对于，如图，取正方形对角线交点为，即为该二十四等边体的外接球球心，
在等腰中，，
在正方形中，，
即外接球半径，
该二十四等边体的外接球的表面积，D正确．

故选：．
依题意补齐正方体，对于，假设平面，得到，根据六边形为正六边形，，得出矛盾判断；对于，结合几何图形，该二十四等边体的体积为正方体体积去掉八个三棱锥体积，从而求出；对于，由平移法找出异面直线所成角为，判断；对于，取正方形对角线交点为，即为该二十四等边体的外接球球心，从而求出半径大小，进而求出外接球体积，判断．
本题考查了立体几何的综合应用，属于中档题．
 9.【答案】 【解析】解：由折线统计图可知不大于的有，，，，，，，，，日共天，
即有天空气质量为“优良”，且上旬的空气优良的天数比中旬的多天，即上旬的空气质量比中旬的好，故A正确；
空气质量最好的是月日，最差的是月日，故B错误；
因为有天不大于，将数据从小到大排列，可知第个数接近，
第个数大于，且比第个数更远离，故中位数大于，故C正确；
由折线统计图可知上旬的数据的极差不超过，且数据比较集中，
中旬的数据极差大于，且数据比较分散，故中旬的方差更大，故D错误；
故选：．
根据折线统计图一一分析即可判断．
本题考查统计数据的折线图，是基础题．
 10.【答案】 【解析】解：，则，
对于，，则，正确；
对于，，则，则，B正确；
对于，，C错误；
对于，，D正确．
故选：．
利用复数的运算法则、共轭复数的定义即可得出．
本题考查了复数代数形式的四则运算，考查了共轭复数的概念，是基础题．
 11.【答案】 【解析】解：在正方体中，线段上有两个动点，，且为正常数，
对于，，，，平面，
平面，，故A正确；
对于，与是异面直线，线段上不存在点，，使得，故B错误；
对于，设到的距离为，则是正的高，设到的距离为，则，
设，则，，
的面积与的面积之比为：，故C正确；
对于，当在线段上运动时，的面积不变，点到平面的距离不变，
三棱锥的体积为定值，故D正确．
故选：．
对于，由，，得平面，从而；对于，由与是异面直线，得线段上不存在点，，使得；对于，到的距离是正的高，到的距离是，由此能判断；对于，的面积不变，点到平面的距离不变，从而三棱锥的体积为定值．
本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．
 12.【答案】 【解析】解：选项A：若，则，则，故A正确；
选项B：令，则，
所以，
令，则，
所以，
即，故B不正确；
选项C：设，
则，
不妨设，，则，
当时，，即，
，所以不存在，故C不正确；
选项D：设，则，
因为，
所以，
所以定值，故D正确．
故选：．
以为基底，按题中要求表示出相关的向量，用数量积的公式计算即可．
本题考查了向量的运算，及数形结合思想方法的运用，是中档题．
 13.【答案】 【解析】解：由题意，该单位青年职工所占的比例为，
可得该单位青年职工被抽取的人数为，
故答案为：．
先求出该单位青年职工所占的比例，再用样本容量乘以此比例，即为所求．
本题主要考查分层抽样的定义和方法，属于基础题．
 14.【答案】 【解析】解：，，
，，则，
，，则，
，
可得．
故答案为：．
由已知可得，，，进一步得到，再由已知定义求解．
本题考查数量积求向量的夹角，考查向量叉乘的模的求法，考查运算求解能力，是基础题．
 15.【答案】 【解析】解：圆台的轴截面面积为，母线与底面所成的角为，如图，

设下底面圆半径为，上底面圆半径为，圆台的高为，
过点作，交于点，
在中，，，
，，
则圆台轴截面的面积，
则圆台的侧面积为．
故答案为：．
作出圆台的轴截面图形，根据其几何特征写出轴截面面积的表达式，再根据圆台的侧面积公式直接代入求解即可．
本题考查圆台的结构特征、圆台侧面积公式等基础知识，考查运算求解能力，是基础题．
 16.【答案】  【解析】解：根据已知条件，作出图形，如下，

取的中点，连接，，
在中，，
，
在中，，
，
，且，
，
为异面直线与所成的角或补角，
为二面角的平面角，，
又，
；
连接，如下图，

点为的重心，在中线上，且，
过点作交的延长线于点，连接，过点作交于点，
，，，又平面，平面，
平面，平面，，
又平面，平面，，
平面，平面，
在中，，
，
在中，，，
．
故答案为：．
对于第一空，取的中点，连接，，根据平移法得出为异面直线与所成的角或补角，根据二面角的平面角定义得出为二面角的平面角，进而利用解三角形知识求；对于第二空，利用等体积法将转化为，结合点为的重心则有，再根据线面垂直的判定定理得出平面，从而得到平面，进而确定出为所求几何体的高，再通过解三角形知识以及体积公式进行求解即可．
本题考查了异面直线所成角和三棱锥的体积计算，属于中档题．
 17.【答案】解：，，
又，且，
，即，
；
，
，
与的夹角的余弦值为． 【解析】由已知，可得，又，结合，利用求得，再由向量模的运算公式求解；
求得，再由数量积求夹角公式可得与的夹角的余弦值．
本题考查平面向量的数量积、平面向量夹角与模的运算等基础知识，考查推理论证能力、运算求解能力，是中档题．
 18.【答案】解：已知的三个内角，，所对的边分别是，，，
求证：．
证明：如图，

由三角形法则有，
所以，
，
因为，
所以，
因为，，
由余弦定理得，
所以，
由正弦定理，
得． 【解析】利用，两边平方可得结论．
由已知可得，进而由余弦定理可求，进而由正弦定理可求．
本题主要考查平面向量的应用、正弦定理、余弦定理及三角恒等变换等基础知识；考查推理论证能力、运算求解能力等；考查化归与转化思想、函数与方程思想等；考查数学运算、逻辑推理等核心素养，体现基础性、综合性．
 19.【答案】解：在频率分布直方图中，由，，
所以中位数位于内，设中位数为，则，
解得，即本次测评分数的中位数约为，
由频率分布直方图可知，
本次测评分数的平均数为
即本次测评分数的平均数约为．
在频率分布直方图中，前组频率之和为，小于，故第百分位数位于第组，
所以，
即第百分位数约为，
由频率分布直方图知测评分在分以上的频率为，
所以估计该市居民测评分在分以上的人数约为万人． 【解析】利用频率分布直方图以及样本数字特征知识可解．
本题主要考查频率分布直方图、平均数、方差、中位数、分位数等基础知识；考查运算求解能力、推理论证能力、应用意识、创新意识等；考查统计与概率思想、分类与整合思想、化归与转化思想等；考查数据分析、数学运算等核心素养，体现综合性、应用性．属于中档题．
 20.【答案】证明：连接交于点，连接，
因为四边形为矩形，所以为的中点，
在中，为的中点，所以，
又因为平面，平面，
所以平面．
因为平面，平面，所以．
又因为，平面，平面，，
所以平面，
又因为平面，所以，
因为，所以矩形为正方形，所以，
又因为平面，平面，．
所以平面C.
又因为平面，所以，
因为，所以．
因为，为的中点，所以，
所以，
所以B. 【解析】利用中位线等相关知识可证，
利用线面垂直可推线线垂直．
本题主要考查空间直线与平面的位置关系等基础知识；考查空间想象能力、推理论证能力、运算求解能力等；考查化归与转化思想、数形结合思想等；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性、综合性，属于中档题．
 21.【答案】解：解法一：选．
所以 ，分
又，所以，分
由正弦定理得，分
因为，所以；分
解法二：选．
所以由正弦定理得，分
所以，分
所以，分
因为，所以，分
又因为，所以；分
解法三：选．
在中，由正弦定理，分
得，分
因为，所以，分
因为，所以；分
解法一：因为，所以，
即，分
所以，分
所以，分
又，所以，解得或，又，所以，分
在中，由余弦定理得，所以分
由正弦定理得，所以，分
所以外接圆的面积分
解法二：因为，所以设，
则，，在中，由余弦定理得，
即分
在中，由余弦定理得，
即，分
由得：，
又，所以分
在中，由余弦定理得，分
又，所以，
由解得，所以，分
在中，由正弦定理得，所以分
所以外接圆的面积分 【解析】解法一：选，由正弦定理结合诱导公式化简，可求出的值；
解法二：选，由正弦定理结合两角和的正弦定理化简可求出的值；
解法三：选，由正弦定理化简，可求出的值；
解法一：由，得出，对其两边同时平方可求出，再由余弦定理求出，可求出外接圆的半径，即可求出答案．
解法二：因为，所以设，在，中，由余弦求出，在中，由余弦定理得，两式求解可得出，求出，可求出外接圆的半径，即可求出答案．
本小题主要考查正弦定理、余弦定理、平面向量及三角恒等变换等基础知识；考查推理论证能力、运算求解能力等；考查化归与转化思想、函数与方程思想等；考查数学运算、逻辑推理等核心素养，体现基础性、综合性．
 22.【答案】证明：在中，，为的中点，所以，
因为平面平面平面平面，，平面，所以平面，
因为平面，所以，
因为平面，平面，，
所以平面；
解：取的中点，连接，，

在中，，所以，
因为平面平面，平面平面，
平面，所以平面，
所以为直线与平面所成的角，
在中，，
所以，
在中，，
所以，
因为，平面，平面，所以平面，
设平面平面，平面，，
所以，
取的中点，连接，，
在中，，所以，所以，
所以为侧面与侧面所成的角，
在中，，所以，
所以侧面与侧面所成的角为． 【解析】依题意可得，再由面面垂直的性质得到平面，即可得到，从而得证；
取的中点，连接，，可证平面，则为直线与平面所成的角，即可求出，取的中点，连接，，即可得到为侧面与侧面所成的角，从而得解．
本题考查了线面垂直的证明和二面角的计算，属于中档题．