2021-2022学年广东省汕头市金平区八年级（下）期末数学试卷（word版含解析）

2021-2022学年广东省汕头市金平区八年级（下）期末数学试卷

学校:___________姓名：___________班级：___________考号：___________

一、选择题（本大题共10小题，共30.0分）

1. 下列二次根式中，属于最简二次根式的是(    )

A.  B.  C.  D.

2. 在下列以线段、、的长为三边的三角形中，不能构成直角三角形的是(    )

A. ：：：： B. ，，
C. ，， D. ，，

3. 广东省今年月日部分城市的最高气温如表：

则这个市区该日最高气温的众数和中位数分别是(    )

A. ， B. ， C. ， D. ，

4. 已知、是直线上的两点，则，的大小关系是(    )

A.  B.  C.  D. 无法比较

5. 下列计算正确的是(    )

A.  B.
C.  D.

6. 如图，▱中，的平分线交于，，，则的长(    )

A.  B.  C.  D.

7. 如图，一次函数的图象经过二、三、四象限，则的取值范围是(    )

A.
B.
C.
D.

8. 已知数据，，，，，，则下列关于这组数据的说法错误的是(    )

A. 众数是 B. 平均数是 C. 方差是 D. 中位数是

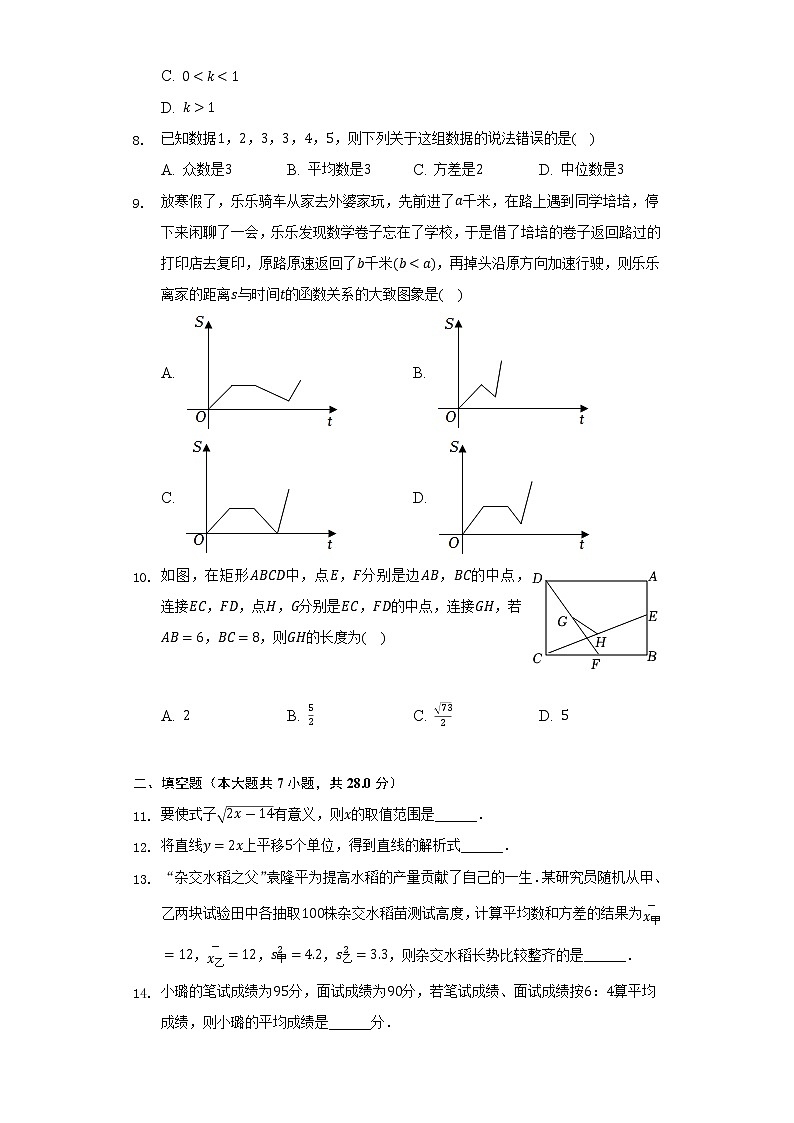
9. 放寒假了，乐乐骑车从家去外婆家玩，先前进了千米，在路上遇到同学培培，停下来闲聊了一会，乐乐发现数学卷子忘在了学校，于是借了培培的卷子返回路过的打印店去复印，原路原速返回了千米，再掉头沿原方向加速行驶，则乐乐离家的距离与时间的函数关系的大致图象是(    )

A.  B.
C.  D.

10. 如图，在矩形中，点，分别是边，的中点，连接，，点，分别是，的中点，连接，若，，则的长度为(    )

A.  B.  C.  D.

二、填空题（本大题共7小题，共28.0分）

11. 要使式子有意义，则的取值范围是______．
12. 将直线上平移个单位，得到直线的解析式______．
13. “杂交水稻之父”袁隆平为提高水稻的产量贡献了自己的一生．某研究员随机从甲、乙两块试验田中各抽取株杂交水稻苗测试高度，计算平均数和方差的结果为，，，，则杂交水稻长势比较整齐的是______．
14. 小璐的笔试成绩为分，面试成绩为分，若笔试成绩、面试成绩按：算平均成绩，则小璐的平均成绩是______分．
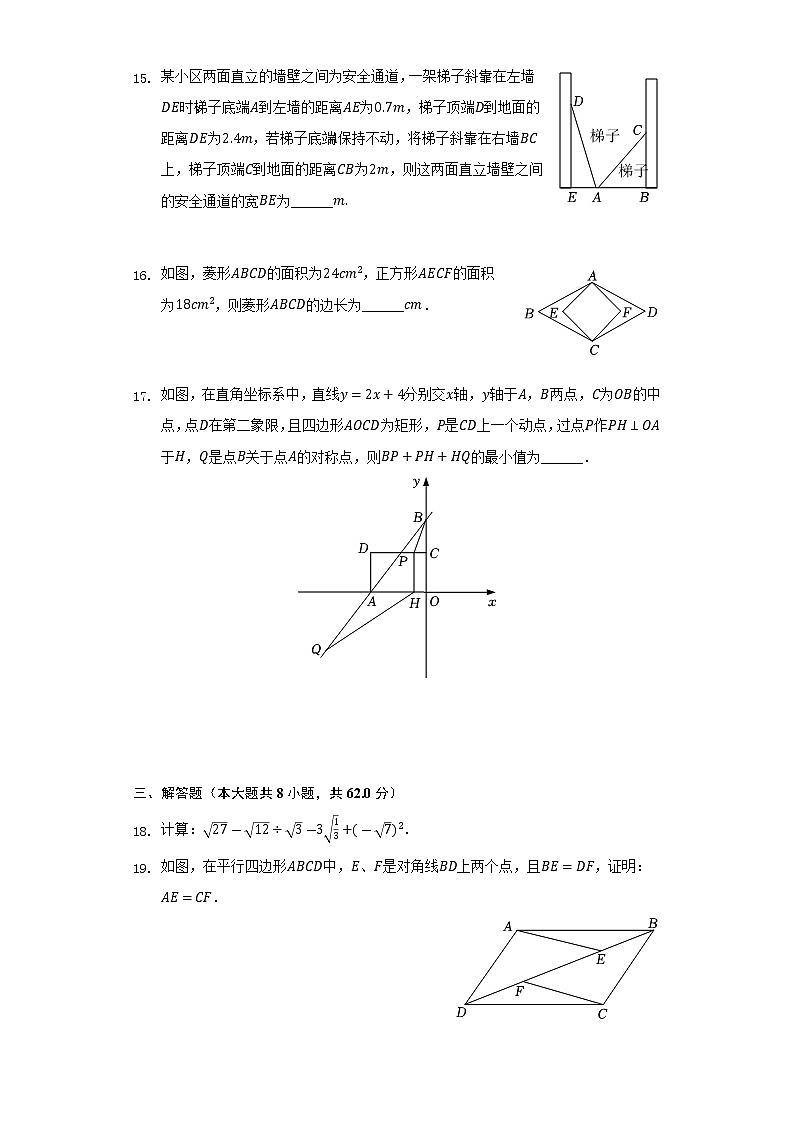
15. 某小区两面直立的墙壁之间为安全通道，一架梯子斜靠在左墙时，梯子底端到左墙的距离为，梯子顶端到地面的距离为，若梯子底端保持不动，将梯子斜靠在右墙上，梯子顶端到地面的距离为，则这两面直立墙壁之间的安全通道的宽为______

16. 如图，菱形的面积为，正方形的面积为，则菱形的边长为______．

17. 如图，在直角坐标系中，直线分别交轴，轴于，两点，为的中点，点在第二象限，且四边形为矩形，是上一个动点，过点作于，是点关于点的对称点，则的最小值为______．

三、解答题（本大题共8小题，共62.0分）

18. 计算：．
19. 如图，在平行四边形中，、是对角线上两个点，且，证明：．

20. 如图，一高层住宅发生火灾，消防车立即赶到距大厦米的长处，升起云梯到火灾窗口，云梯长米，云梯底部距地面米的长，问：发生火灾的住户窗口距离地面有多高的长？

21. 金平区为了加强社区居民对防疫的了解，通过网络宣传防疫知识，并鼓励社区居民在线参与作答防疫知识模拟试卷，社区工作人员随机从甲、乙两个社区各抽取名人员的答卷成绩，并对他们的成绩单位：分进行统计、分析，过程如下：
    收集数据：
    甲区：
    乙区：
    整理数据：

分析数据：

应用数据：
填空：______，______，______，______；
若甲区共有人参与答卷，请估计甲区成绩大于分的人数；
根据以上数据分析，你认为甲、乙两个区哪一个对防疫知识掌握更好？请写出理由．

22. 如图，网格是由小正方形拼成，每个小正方形的边长都为四边形的四个点都在格点上．
    四边形的面积为______，周长为______；
    求证：是直角．

23. 凤凰单丛枞茶，是潮汕的名茶，已有九百余年的历史．潮汕人将单丛茶按香型分为黄枝香、芝兰香、桃仁香、玉桂香、通天香、鸭屎香等多种．清明采茶季后，某茶叶店准备购买通天香和鸭屎香两种单丛茶进行销售，已知若购买千克通天香单丛和千克鸭屎香单丛需要元，购买千克通天香单丛和千克鸭屎香单丛需要元．
    求通天香、鸭屎香两种茶叶的单价分别为多少元？
    茶叶专卖店计划购买通天香、鸭屎香两种单丛茶共千克，总费用不多于元，并且要求通天香茶叶数量不能低于千克，那么应如何安排购买方案才能使总费用最少，最少费用应为多少元？
24. 已知：在边长为的正方形中，点为对角线上一点，且将三角板的直角顶点与点重合，一条直角边与直线交于点，另一条直角边与射线交于点点不与点重合，将三角板绕点旋转．
    如图，当点、在线段、上时，求证：；
    当时，求的面积；
    当为等腰三角形时，直接写出线段的长．
     

25. 如图，在平面直角坐标系中，直线的解析式为，它与轴交于点，与轴交于点，直线与直线交于点动点从点出发，以每秒个单位长度的速度沿射线运动，运动时间为秒．
    求的面积；
    设的面积为，求与的函数关系式；
    是直线上一点，在平面内是否存在点，使以，，，为顶点的四边形是菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．
     

答案和解析

1.【答案】 

【解析】解：选项，原式，故该选项不符合题意；
选项，原式，故该选项不符合题意；
选项，原式，故该选项不符合题意；
选项，是最简二次根式，故该选项符合题意；
故选：．
根据最简二次根式的概念：被开方数不含分母；被开方数中不含能开得尽方的因数或因式判断即可．
本题考查了最简二次根式，掌握最简二次根式的概念：被开方数不含分母；被开方数中不含能开得尽方的因数或因式是解题的关键．
 

2.【答案】 

【解析】解：、设，，，
，，
，
故A不符合题意；
B、，，
，
以线段，，的长为三边不能构成直角三角形，
故B符合题意；
C、，，
，
以线段，，的长为三边能构成直角三角形，
故C不符合题意；
D、，，
，
以线段，，的长为三边能构成直角三角形，
故D不符合题意；
故选：．
根据勾股定理的逆定理，进行计算即可解答．
本题考查了勾股定理的逆定理，在应用定理时，应先认真分析所给边的大小关系，确定最大边后，使两条较小边的平方和等于最大边的平方．
 

3.【答案】 

【解析】解：将这组数据重新排列为、、、、、、、，
所以这组数据的众数为，中位数是，
故选：．
根据众数和中位数的定义求解即可．
本题主要考查众数、中位数，一组数据中出现次数最多的数据叫做众数；将一组数据按照从小到大或从大到小的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
 

4.【答案】 

【解析】解：，
随的增大而增大，
，
，
故选：．
根据，一次函数随的增大而增大即可判断．
本题主要利用一次函数的性质：当时，随的增大而增大，当时，随的增大而减小．
 

5.【答案】 

【解析】解：、，故A不符合题意；
B、与不能合并，故B不符合题意；
C、，故C符合题意；
D、，故D不符合题意；
故选：．
根据二次根式的加法，乘法，除法，二次根式的性质，进行计算逐一判断即可解答．
本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．
 

6.【答案】 

【解析】解：四边形是平行四边形，
，，
，
平分，
，
，
，
．
故选：．
由平行四边形的性质可得，由平行线的性质和角平分线的性质可求，即可求解．
本题考查了平行四边形的性质，角平分线的性质，求出的长是本题的关键．
 

7.【答案】 

【解析】解：一次函数的图象经过二、三、四象限，
，
解得，
故选：．
根据一次函数的图象经过二、三、四象限，可知且，然后即可求得的取值范围．
本题考查一次函数图象与系数的关系，解答本题的关键是明确一次函数的性质，写出相应的不等式组．
 

8.【答案】 

【解析】解：六个数中出现了两次，次数最多，即众数为；
由平均数的公式得平均数；
方差；
将六个数按从小到大的顺序排列得到中间两个数均为，则中位数为．
故选：．
分别求出这组数据的平均数、中位数和众数、方差即可求解．
此题考查了学生对方差，平均数，中位数，众数的理解．只有熟练掌握它们的定义，做题时才能运用自如．
 

9.【答案】 

【解析】解：、乐乐原路原速返回，图象与原来的图象倾斜度相同，所以选项错误；
B、休息了一段时间，表明中间有一段图象与横轴平行，所以选项错误；
C、休息了一段时间，又沿原路原速返回了千米，由于，所以没回到出发地，图象与横轴没交点，所以选项错误；
D、先前进了千米，对应的图象为正比例函数图象；休息了一段时间，对应的图象为横轴平行的线段；沿原路原速返回了千米，对应的图象为一次函数图象，随的增大而减小且与横轴没交点；掉头沿原方向加速行驶，对应的图象为一次函数图象，随的增大而增大，并且图象更陡，所以选项正确．
故选：．
分四段看图象，然后根据每段图象大致位置进行判断．
本题考查了函数图象：利用函数图象能直观地反映两变量的变化情况．
 

10.【答案】 

【解析】解：连接并延长交于，连接，

是的中点，
，
四边形是矩形，
，
，
在和中，
，
≌，
，，
，
点是的中点，
，
在中，由勾股定理得，，
、是、的中点，
是的中位线，
，
故选：．
连接并延长交于，连接，首先证明≌，得，，再利用勾股定理求出的长度，再根据三角形中位线定理可得答案．
本题主要考查了矩形的性质，全等三角形的判定与性质，勾股定理，三角形中位线定理等知识，作辅助线构造三角形中位线是解题的关键．
 

11.【答案】 

【解析】解：由题意得：，
解得：，
故答案为：．
根据二次根式的被开方数是非负数列出不等式，解不等式即可．
本题考查的是二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．
 

12.【答案】 

【解析】解：直线上平移个单位，得到直线的解析式为，
故答案为：．
根据“上加下减”的原则进行解答即可．
本题考查的是一次函数的图象与几何变换，熟知“上加下减”的原则是解答此题的关键．
 

13.【答案】乙 

【解析】解：，，，，
，
杂交水稻长势比较整齐的是乙，
故答案为：乙．
根据方差的定义，方差越小数据越稳定即可求解．
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
 

14.【答案】 

【解析】解：小璐的平均成绩分．
故答案为：．
根据加权平均数的计算公式计算可得．
本题考查加权平均数，解答本题的关键是明确题意，利用加权平均数的计算方法解答．
 

15.【答案】 

【解析】解：在中，，米，米，
．
在中，
，米，，
，
米．
米．
答：小巷的宽度为米，
故答案为：．
先根据勾股定理求出的长，同理可得出的长，进而可得出结论．
本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
 

16.【答案】 

【解析】解：因为正方形的面积为，
所以，
因为菱形的面积为，
所以，
所以菱形的边长．
故答案为：．
根据正方形的面积可用对角线进行计算解答即可．
此题考查正方形的性质，关键是根据正方形和菱形的面积进行解答．
 

17.【答案】 

【解析】解：如图，连接，


直线分别交轴，轴于，两点，
，，
是的中点，
，
，
四边形是矩形，
，
，
四边形是平行四边形，
，
，
要使的值最小，只需、、三点共线即可，
点是点关于点的对称点，
，
又点，
根据勾股定理可得，
此时，，
即的最小值为；
故答案为：．
根据直线先确定和的长，证明四边形是矩形，得，再证明四边形是平行四边形，则，在中，是定值，所以只要的值最小就可以，当、、在同一直线上时，的值最小，利用平行四边形的性质求出即可．
本题考查了一次函数点的坐标的求法、三角形面积的求法和三点共线及最值，综合性强．
 

18.【答案】解：原式

． 

【解析】先根据二次根式的除法法则和二次根式的性质计算，然后化简后合并即可．
本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的除法法则是解决问题的关键．
 

19.【答案】证明：四边形是平行四边形，
，，
，
在和中，
，
≌，
． 

【解析】由平行四边形的性质可得，，由“”可证≌，可得结论．
本题考查了平行四边形的性质，全等三角形的判定和性质，证明三角形全等是解题的关键．
 

20.【答案】解：由题意可知，，米，米，米，
在中，根据勾股定理得：米，
米；
答：发生火灾的住户窗口距离地面米． 

【解析】根据勾股定理求出的长，即可得出结论．
此题主要考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．
 

21.【答案】       

【解析】解：由乙小区抽取的名人员的答卷成绩得，
由乙小区抽取的名人员的答卷成绩得，
把甲小区抽取的名人员的答卷成绩排从小到大排列，排在中间的两个数分别为、，故中位数，
乙小区抽取的名人员的答卷成绩中出现次数最多的是，故众数．
故答案为：，，，；
估计甲区成绩大于分的人数为人；
乙区对防疫知识掌握更好，
理由：乙区的平均数、中位数、众数均大于甲区的．
由乙小区抽取的名人员的答卷成绩得；根据乙小区抽取的名人员的答卷成绩得，根据中位数和众数的定义可得和的值；
用样本估计总体即可；
依据表格中平均数、中位数、众数，做出判断即可．
本题考查了众数、中位数、平均数、频数分布表、用样本估计总体等知识；熟练掌握众数、中位数的定义是解题的关键．
 

22.【答案】  

【解析】解：由题意得：
四边形的面积

，
，
，
，
，
，，，，
四边形的周长，
四边形的面积为，周长为，
故答案为：，；
证明：连接，

由题意得：
，
，
，
是直角三角形，
是直角．
根据题意可得四边形的面积，然后进行计算即可解答，再利用勾股定理求出，，，的长，从而求出四边形的周长；
连接，利用勾股定理求出，再根据勾股定理的逆定理进行计算，可证是直角三角形，即可解答．
本题考查了勾股定理，勾股定理的逆定理，熟练掌握勾股定理，以及勾股定理的逆定理是解题的关键．
 

23.【答案】解：设通天香单丛每千克为元，鸭屎单丛每千克为元，根据“购买千克通天香单丛和千克鸭屎香单丛需要元，购买千克通天香单丛和千克鸭屎香单丛需要元”，得，
解得，
通天香单丛每千克为元，鸭屎香单丛每千克为元．
设购买通天香单丛千克，鸭屎香单丛千克，总费用元，
根据题意，得，
解得，
，
的取值范围是：，
总费用，
，
随着的增大而增大，
当时，最少，最少元，
通天香单丛购进千克，鸭屎香单丛购进千克，总费用最少为元． 

【解析】设通天香单丛每千克为元，鸭屎单丛每千克为元，根据“购买千克通天香单丛和千克鸭屎香单丛需要元，购买千克通天香单丛和千克鸭屎香单丛需要元”列方程组解答即可；
设购买种茶叶千克，种茶叶千克，总费用元，根据题意得出与的函数关系式，列出不等式求出的取值范围，再根据一次函数的性质解答即可．
本题考查了一次函数的实际应用，涉及二元一次方程组的应用，一元一次不等式的应用，根据题意建立关系式是解题的关键，本题综合性较强．
 

24.【答案】证明：如图，过点作，，垂足分别为点、．

四边形为正方形，
平分，
．
四边形为正方形．
，
，
，
即．
在和中，
，
≌，
．
解：如图，过点作于点，

当时，，
在中，设，
则，
在中，，
，
，
解得：．
．
解：的长为、或．
Ⅰ：当点在射线上时，
如图，当，

，
，
，
．
当时，则，
为等腰直角三角形，与重合，舍去．
如图，当时，
同理可证≌，

，
，
，
．
Ⅱ：当点在延长线上时，
，
只有，如图，

同理可证：≌，
．
，
，
，
．
综上所述，的长为或或． 

【解析】如图，过点作，，垂足分别为点、由正方形的性质可证≌，即可证明；
由直角三角形的性质求出的长，则可求出答案；
分两种情况，Ⅰ：当点在射线上时，Ⅱ：当点在延长线上时，由勾股定理及等腰直角三角形的性质可求出答案．
本题考查了正方形的性质、勾股定理、三角形面积计算、等腰三角形的判定与性质、全等三角形的判定与性质以及分类讨论的数学思想的运用，综合运用这些性质、判定进行推理是解题的关键．
 

25.【答案】解：直线：与轴交于点，
令，得，
，
，
直线与直线：交于点，
，
解得
，
；
设点的坐标为，由题意得，
过作轴上，过作于，如图，

，，
，
，
点的坐标为，
，
当，
，
当，
，
与的函数关系式为：；
存在点，使以，，，为顶点的四边形是菱形，
，
，
当为菱形的边时，即，如图，

当点在点上方时，
四边形是菱形，
，
直线：，
，
，
，
同理，当点在的下方时，，
；
当时，
则四边形是正方形，
所以；
当为菱形的对角线时，连接，

四边形是菱形，
，、互相平分，
点、的纵坐标为，
直线：，是直线上一点，
，
，
综上所述，存在点，使以，，，为顶点的四边形是菱形，点的坐标为：或或或． 

【解析】首先根据直线解析式求出交点的坐标，从而得出的面积；
由题意得，根据的长度，表示出点的坐标，再分点在线段上或点在射线上，分别表示出与的函数解析式即可；
分为菱形的边和对角线两种情形，分别画出求出，从而解决问题．
本题是一次函数综合题，主要考查了两直线的交点问题，三角形的面积，菱形的判定与性质等知识，运用分类讨论思想是解决问题的关键．