九年级中考数学专题复习课件 手拉手模型

这是一份九年级中考数学专题复习课件 手拉手模型，共13页。PPT课件主要包含了DE与BG的数量关系，AD与EC的数量关系，BD与AE的数量关系，BD与EC的数量关系，谈谈自己的收获，总结升华等内容，欢迎下载使用。

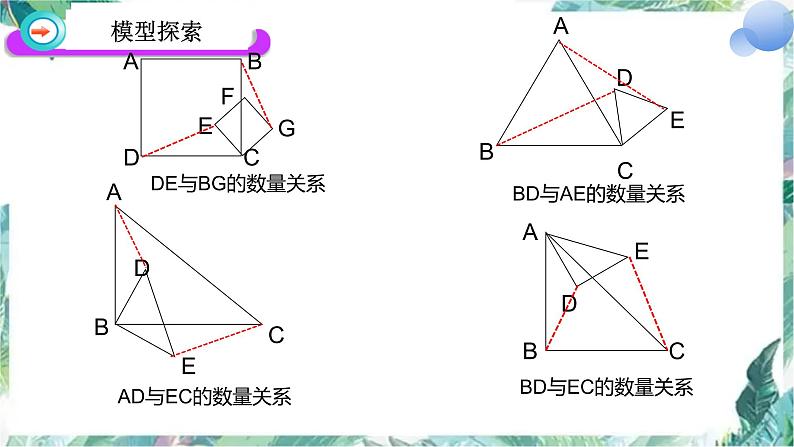
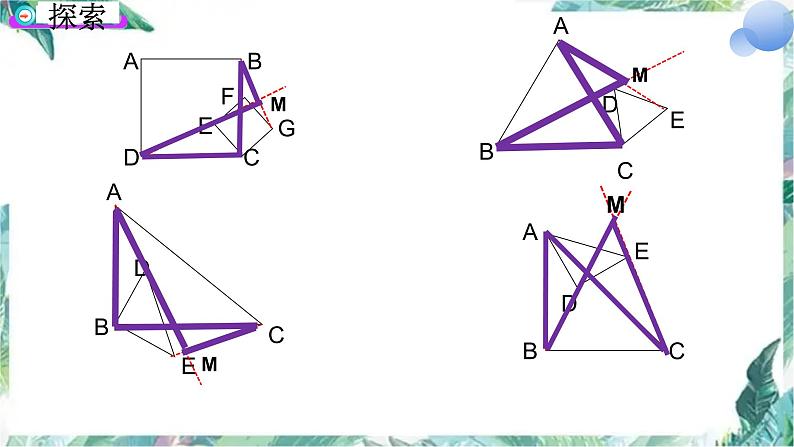
已知：有公共对应顶点的一对全等或相似图形，称为“手拉手”模型，连接其他对应顶点；结论：得到一对全等(或相似)三角形；
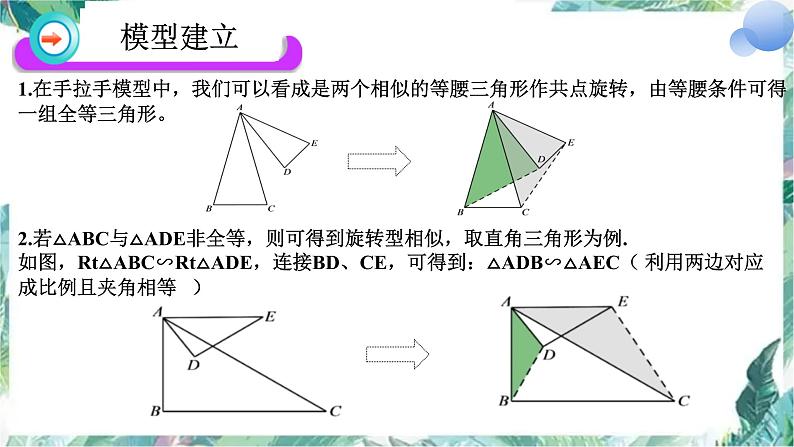
1.在手拉手模型中，我们可以看成是两个相似的等腰三角形作共点旋转，由等腰条件可得一组全等三角形。
2.若△ABC与△ADE非全等，则可得到旋转型相似，取直角三角形为例.如图，Rt△ABC∽Rt△ADE，连接BD、CE，可得到：△ADB∽△AEC（ 利用两边对应成比例且夹角相等 ）
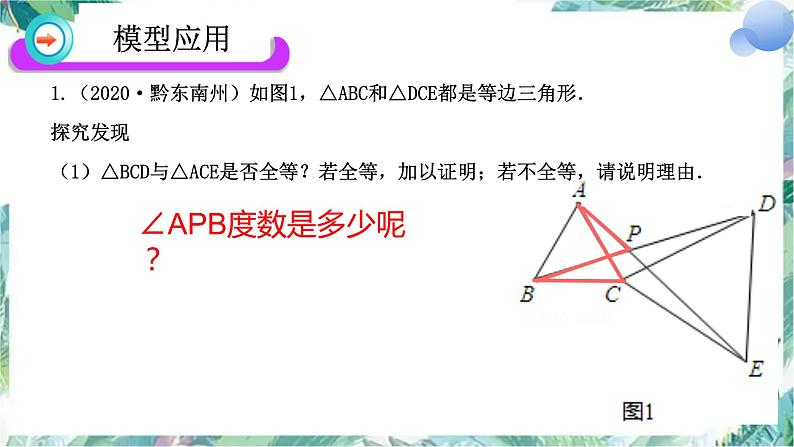
1.（2020·黔东南州）如图1，△ABC和△DCE都是等边三角形．探究发现（1）△BCD与△ACE是否全等？若全等，加以证明；若不全等，请说明理由．
∠APB度数是多少呢？
3.（临沂中考）如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交CD于点F．另一边交CB的延长线于点G．（1）求证：EF=EG；
（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，那么（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由；
（3）如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求 的值
1. 如图1，AB＝AC，AD＝AE,∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_______
2. 如图2，在△ABC与△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE，连接BD、CE，可得△ABC∽△ADE，若 ＝ ，则 的值___
1.识别手拉手模型2.相似必成双，要能找到产生的新相似3.结合两对相似，利用对应角相等，对应边成比例等相关知识解决