高考数学二轮复习第2部分专题篇素养提升文理专题二数列文理第2讲数列求和及其综合应用文理学案含解析

第2讲　数列求和及其综合应用(文理)

JIE TI CE LUE MING FANG XIANG

解题策略·明方向　

⊙︱考情分析︱

1．高考对数列求和的考查主要以解答题的形式出现，通过分组转化、错位相减、裂项相消等方法求数列的前n项和，难度中等偏下．

2．在考查数列求和的同时，将数列与函数、不等式交汇渗透．

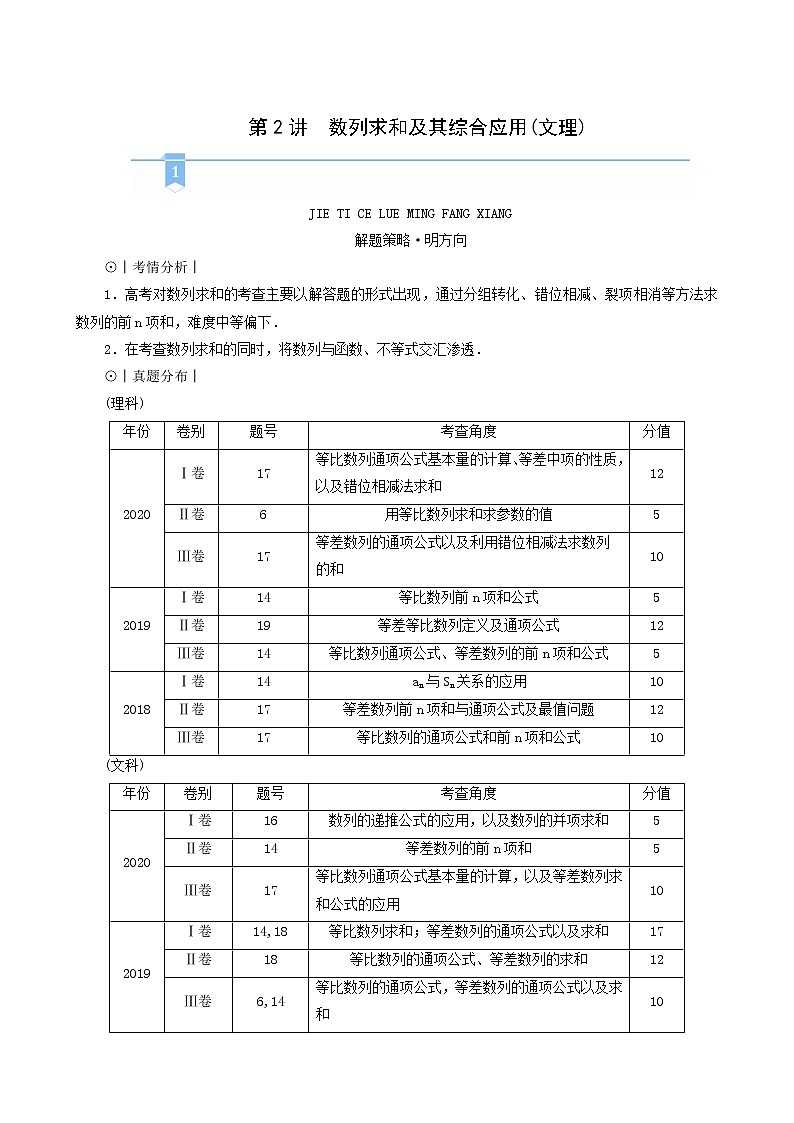
⊙︱真题分布︱

(理科)

(文科)

KAO DIAN FEN LEI XI ZHONG DIAN

考点分类·析重点　

考点一　数列的通项公式

1．数列通项an与前n项和Sn的关系，

an＝

2．应用an与Sn的关系式f(an，Sn)＝0时，应特别注意n＝1时的情况，防止产生错误．

典例1　(1)(2019·淄博三模)已知正项数列{an}满足a1＝1，(n＋2)a－(n＋1)a＋anan＋1＝0，则它的通项an＝(　B　)

A．　　 B．

C．　　 D．n

(2)设数列{an}满足a1＋3a2＋…＋(2n－1)an＝2n，则an＝____.

【解析】　(1)由(n＋2)a－(n＋1)a＋anan＋1＝0，

可得[(n＋2)an＋1－(n＋1)an]×(an＋1＋an)＝0

又因为an>0，所以＝.

又a1＝1，则an＝··…··a1

＝··…··1＝.故选B．

(2)因为a1＋3a2＋…＋(2n－1)an＝2n，

故当n≥2时，a1＋3a2＋…＋(2n－3)an－1＝2n－1．

两式相减得(2n－1)an＝2n－1，所以an＝(n≥2)．

由题设可得a1＝2，不满足上式，

所以数列{an}的通项公式为an＝

求数列的通项公式的基本类型

(1)利用an＝直接求解，或者据此得出数列的递推式求解，特别是已知Sn＝kan＋b(k≠0,1，b≠0)时可得数列{an}一定是等比数列．

(2)三种简单的递推数列：an＋1－an＝f(n)，＝f(n)，an＋1＝pan＋q(p≠0,1，q≠0)，第一个使用累加的方法、第二个使用累积的方法、第三个可以使用待定系数法化为等比数列(设an＋1＋λ＝p(an＋λ)，展开比较系数得出λ)．

(3)周期数列，通过验证或者推理得出数列的周期性后得出其通项公式．

1．(2019·洛阳三模)在数列{an}中，a1＝2，an＋1＝an＋ln (1＋)，则an＝(　A　)

A．2＋ln n　　 B．2＋(n－1)ln n

C．2＋nln n　　 D．1＋n＋ln n

【解析】　因为an＋1－an＝ln＝ln(n＋1)－lnn，所以an＝(an－an－1)＋(an－1－an－2)＋…＋(a2－a1)＋a1＝ln n－ln (n－1)＋ln (n－1)－ln (n－2)＋…＋ln 2－ln 1＋2＝2＋ln n．故选A．

考点二　数列的求和问题

1．数列求和的常见方法

(1)分组求和法：形如an±bn，{an}，{bn}是等差或等比数列)的形式．

(2)裂项相消法：形如或其它特殊分式的形式．

2．常用的裂项公式

(1)若{an}是等差数列，则＝，＝；

(2)＝－，＝；

(3)＝；

(4)＝；

(5)＝－，＝(－)．

(6)＝－(m≠0)

3．错位相减法：形如{anbn}形式(其中{an}为等差，{bn}为等比)．

4．倒序相加法：首、尾对称的两项和为定值的形式．

5．并项相加法：正负交替出现的数列形式，对项数n进行分类即分奇偶性．

考向1　裂项相消法求和

典例2　(2020·吉林省重点中学联考)已知各项均为正数的等比数列{an}的首项为，且2(1－a3)＝2a1＋3a2．

(1)求数列{an}的通项公式；

(2)若bn＝8n，数列{bn}的前n项和为Tn，数列{an}的前n项和为Sn，试比较＋＋…＋与Sn的大小．

【解析】　(1)由题意，设an＝a1qn－1(q>0)，则，

解得q＝或q＝－2(舍)，

∴an＝×n－1＝n，即an＝.

(2)由(1)知an＝，∴Sn＝＝1－n.

∵bn＝8n，∴Tn＝4n2＋4n，

∴＝＝，

∴＋＋…＋＝＝<，

又∵Sn＝＝＝，1－≥0，

∴Sn≥，

∴＋＋…＋<Sn.

裂项相消法的基本思想就是把通项an分拆成an＝bn＋k－bn(k≥1，k∈N*)的形式，从而达到在求和时某些项相消的目的，在解题时要善于根据这个基本思想变换数列{an}的通项公式，使之符合裂项相消的条件．

考向2　错位相减法求和

典例3　(2020·百校联盟联考)已知递增的等比数列{an}的前n项和为Sn，a1＋a4＝9，a2a3＝8．

(1)求数列{an}的通项公式；

(2)求数列{n·Sn}的前n项和Tn.

【解析】　(1)由题意，

解得a1＝1，a4＝8或a1＝8，a4＝1；

而等比数列{an}递增，所以a1＝1，a4＝8，

故公比q＝＝2，所以an＝2n－1．

(2)由(1)得到Sn＝1＋2＋…2n－1＝2n－1，

所以n·Sn＝n(2n－1)＝n·2n－n，

Tn＝1×2＋2×22＋3×23＋…＋n·2n－(1＋2＋…＋n)，

设t＝1×2＋2×22＋3×23＋…＋n·2n，

2t＝1×22＋2×23＋3×24＋…＋n·2n＋1，

两式相减可得，－t＝2＋22＋23＋…＋2n－n·2n＋1＝－n·2n＋1

故t＝(n－1)·2n＋1＋2，

所以Tn＝(n－1)·2n＋1＋2－.

应用错位相减法求和的关注点

(1)错位相减法适用于求数列{an·bn}的前n项和，其中{an}为等差数列，{bn}为等比数列．

(2)在写“Sn”与“qSn”的表达式时，应特别注意将两式“错项对齐”，以便下一步准确地写出“Sn－qSn”的表达式．

2．(1)(2020·青海省玉树州高三联考)已知等差数列{an}的前n项和为Sn，且a9＝a12＋6，a2＝4，则数列的前10项和为____.

(2)数列{n·2n＋n}的前n项和为__(n－1)·2n＋1＋__.

(3)(2020·湖南师大附中第二次月考)在公差大于0的等差数列{an}中，2a7－a13＝1，且a1，a3－1，a6＋5成等比数列，则数列{(－1)n－1an}的前21项和为__21__.

【解析】　(1)设等差数列{an}的公差为d，

∵a9＝a12＋6，a2＝4，

∴12＝a1＋5d，又a1＋d＝4，

解得a1＝d＝2，

∴Sn＝2n＋×2＝n(n＋1)．

∴＝＝－.

则数列的前10项和＝1－＋－＋…＋－＝1－＝.

(2)设bn＝n·2n＋n，

所以Tn＝b1＋b2＋b3＋…＋bn＝(2＋2×22＋3×23＋…＋n·2n)＋(1＋2＋3＋…＋n)，

令T＝2＋2×22＋3×23＋…＋n·2n，

则2T＝22＋2×23＋3×24＋…＋n·2n＋1，

两式相减，得

－T＝2＋22＋23＋…＋2n－n·2n＋1＝－n·2n＋1，

所以T＝2(1－2n)＋n·2n＋1＝2＋(n－1)·2n＋1，

因为1＋2＋3＋…＋n＝，

所以Tn＝(n－1)·2n＋1＋.

(3)公差d大于0的等差数列{an}中，2a7－a13＝1，可得2a1＋12d－(a1＋12d)＝1，即a1＝1，由a1，a3－1，a6＋5成等比数列，可得(a3－1)2＝a1(a6＋5)，即为(1＋2d－1)2＝1＋5d＋5，解得d＝2(负值舍去)，

则an＝1＋2(n－1)＝2n－1，n∈N*，

所以数列{(－1)n－1an}的前21项和为a1－a2＋a3－a4＋…＋a19－a20＋a21＝1－3＋5－7＋…＋37－39＋41

＝－2×10＋41＝21．

考点三　与数列相关的综合问题

(1)以数列为背景的不等式恒成立问题，多与数列求和相联系，最后利用数列或数列对应函数的单调性求解．

(2)以数列为背景的不等式证明问题，多与数列求和有关，常转化为数列和的最值问题，同时要注意比较法、放缩法、基本不等式的应用．

(3)如果是解不等式，注意因式分解的应用．

(4)当已知数列关系式时，需要知道其范围时，可借助数列的单调性，即比较相邻两项的大小即可．

典例4　(2019·湖北高三冲刺)已知数列{an}的前n项和为Sn，满足：Sn＝1－an(n∈N*)．

(1)求Sn；

(2)若bn＝－log3(1－Sn＋1)(n∈N*)，Tn＝＋＋＋…＋，则是否存在正整数m，当n≥m时Sn＞Tn恒成立？若存在，求m的最小值；若不存在，请说明理由．

【解析】　(1)当n＝1时，a1＝S1，

由S1＝1－a1，得a1＝.

当n≥2时，Sn＝1－an，Sn－1＝1－an－1，

所以an＝Sn－Sn－1＝－

＝an－1－an，

所以an＝an－1，

所以{an}是以为首项，为公比的等比数列，

所以Sn＝＝1－n.

(2)存在．

由(1)可知，bn＝－log3(1－Sn＋1)

＝－log3＝－log3n＋1

＝n＋1，

所以＝＝－，

所以Tn＝＋＋＋…＋

＝＋＋＋…＋

＝－<.

又Sn＝1－n，

所以{Sn}为递增数列，Sn≥S1＝.

而＞，

所以∀n∈N*恒有Sn＞Tn，故存在正整数m，当n≥m时Sn＞Tn恒成立，其m的最小值为1．

1．求解数列与函数交汇问题注意两点：

(1)数列是一类特殊的函数，其定义域是正整数集(或它的有限子集)，在求数列最值或不等关系时要特别重视．

(2)解题时准确构造函数，利用函数性质时注意限制条件．

2．数列为背景的不等式恒成立、不等式证明，多与数列的求和相联系，最后利用数列或数列对应函数的单调性处理．

3．设f(x)＝x2＋2x，f′(x)是y＝f(x)的导函数，若数列{an}满足an＋1＝f′(an)，且首项a1＝1．

(1)求数列{an}的通项公式；

(2)数列{an}的前n项和为Sn，等比数列{bn}中，b1＝a1，b2＝a2，数列{bn}的前n项和为Tn，请写出适合条件Tn≤Sn的所有n的值．

【解析】　(1)由f(x)＝x2＋2x，得f′(x)＝x＋2．

∵an＋1＝f′(an)，且a1＝1．

∴an＋1＝an＋2则an＋1－an＝2，

因此数列{an}是公差为2，首项为1的等差数列．

∴an＝1＋2(n－1)＝2n－1．

(2)数列{an}的前n项和Sn＝＝n2，

等比数列{bn}中，b1＝a1＝1，b2＝a2＝3，

∴q＝3，∴bn＝3n－1．

∴数列{bn}的前n项和Tn＝＝.

Tn≤Sn可化为≤n2．

又n∈N*，∴n＝1，或n＝2，

故适合条件Tn≤Sn的所有n的值为1和2．

YI CUO QING LING MIAN SHI WU

易错清零·免失误　

1．忽视等比数列中的隐含条件致误

典例1　各项均为实数的等比数列{an}的前n项和为Sn，若S10＝10，S30＝70，则S40＝__150__.

【错解】　150或－200

【剖析】　数列S10，S20－S10，S30－S20，S40－S30的公比q10>0．忽略了此隐含条件，就产生了增解－200．

【正解】　设等比数列{an}的公比为q，

记b1＝S10，b2＝S20－S10，b3＝S30－S20，b4＝S40－S30，

b1，b2，b3，b4是以公比为r＝q10>0的等比数列

∴b1＋b2＋b3＝10＋10r＋10r2＝S30＝70．

∴r2＋r－6＝0，∴r＝2或r＝－3(舍去)．

∴S40＝b1＋b2＋b3＋b4＝＝150．

2．用裂项相消法求和时漏项或添项

典例2　已知数列{an}的前n项和为Sn，a1＝2，点(an＋1，Sn)在直线y＝x－2上(n∈N*)．

(1)求数列{an}的通项公式；

(2)令bn＝，设数列{bn}的前n项和为Tn，求证：≤Tn<.

【解析】　(1)因为点(an＋1，Sn)在直线y＝x－2上，所以an＋1＝2＋Sn(n∈N*)．①

当n≥2时，an＝2＋Sn－1．②

①－②，可得an＋1－an＝Sn－Sn－1＝an(n≥2)，

即an＋1＝2an(n≥2)．

当n＝1时，a2＝2＋S1＝2＋a1，所以a2＝4，则a2＝2a1．

综上，an＋1＝2an(n∈N*)．

所以数列{an}是以2为首项，2为公比的等比数列，所以an＝2n(n∈N*)．

(2)由(1)得an＝2n(n∈N*)，

因为bn＝，

所以bn＝＝，

所以Tn＝

＝.

因为0<≤＝，

所以－≤－<0，所以≤1－<1，所以≤Tn<.

【剖析】　裂项相消法是一种常见的数列求和方法，利用该方法求和时需注意以下几点：一是注意变形的等价性，如本题，＝，不要忘记乘；二是在消项时，正、负项抵消后，应注意是否只余下第一项和最后一项，有时是前面余下两项(或几项)，后面相应也余下两项(或几项)，即剩的项前后位置是对称的；三是掌握一些常见的裂项技巧，如数列{an}是公差为d(d≠0)的等差数列，则＝，又如＝，＝，＝－等．

3．用错位相减法求和时对项的位置处理不当

典例3　(2020·合肥一中10月月考)设等比数列{an}满足a1＋a3＝20，a2＋a4＝10．

(1)令Tn＝a1a2a3…an，求Tn的最大值；

(2)令bn＝log2an，求数列{anbn}的前n项和Sn.

【解析】　(1)设等比数列{an}的公比为q，

因为a1＋a3＝20，a2＋a4＝10，所以解得所以an＝.

方法一：当an≥1时，解得n≤5，

所以a1>a2>a3>a4>a5＝1,1>a6>a7>…，

T4＝T5＝16×8×4×2＝1 024，所以Tn的最大值为1 024．

方法二：若Tn最大，则Tn＋1≤Tn，Tn≥Tn－1，

所以an≥1，且an＋1≤1，所以所以4≤n≤5．

T4＝T5＝16×8×4×2＝1 024，所以Tn的最大值为1 024．

(2)由(1)知an＝，则bn＝log2an＝log2＝5－n，an·bn＝(5－n)·n－5，

Sn＝4·－4＋3·－3＋…＋(5－n)·n－5，①

所以Sn＝4·－3＋3·－2＋…＋(6－n)·n－5＋(5－n)·n－4，②

①－②，得Sn＝4·－4－

－(5－n)·n－4

＝64－－(5－n)·n－4

＝64－16－(5－n)·n－4

＝48＋(n－3)·n－4，

所以Sn＝96＋(n－3)·25－n.

【剖析】　运用错位相减法求和的一般步骤为：一是判断模型，如本题中数列{an}，{bn}一个为等比数列，一个为等差数列；二是错开位置，如本题的②式，向右错开一个位置来书写，这样为两式相减不会看错项做准备；三是相减，如本题中相减时要注意②式中的最后一项的符号，学生常在此处出错，一定要小心．