初中数学北师大版九年级上册2 矩形的性质与判定完美版课件ppt

这是一份初中数学北师大版九年级上册2 矩形的性质与判定完美版课件ppt，文件包含122《矩形的判定》课件PPTpptx、122《矩形的判定》教案docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
1.矩形的定义是什么?
有一个角是直角的平行四边形是矩形。
2.矩形的性质有哪些？从哪些方面考虑的？
矩形既是中心对称图形也是轴对称图形
思考:工人师傅在做门窗或矩形零件时，如何确保图形是矩形呢？现在师傅带了两种工具（卷尺和量角器），他说用这两种工具的任意一种就可以解决问题，这是为什么呢？
这节课我们一起探讨矩形的判定吧.
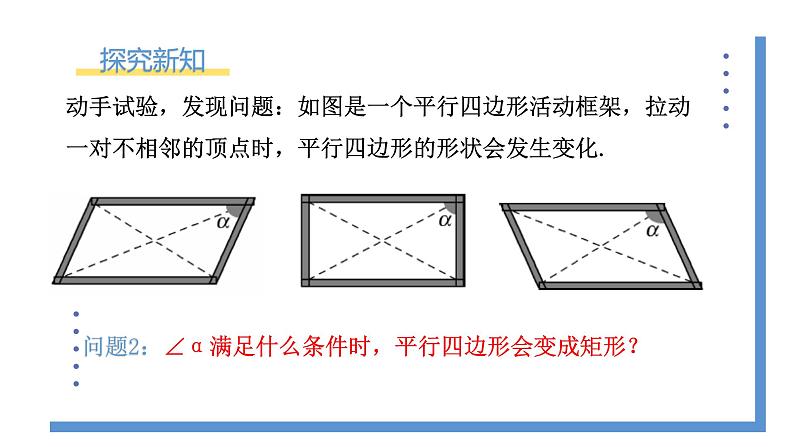
动手试验，发现问题：如图是一个平行四边形活动框架，拉动一对不相邻的顶点时，平行四边形的形状会发生变化.
问题2：∠α满足什么条件时，平行四边形会变成矩形？
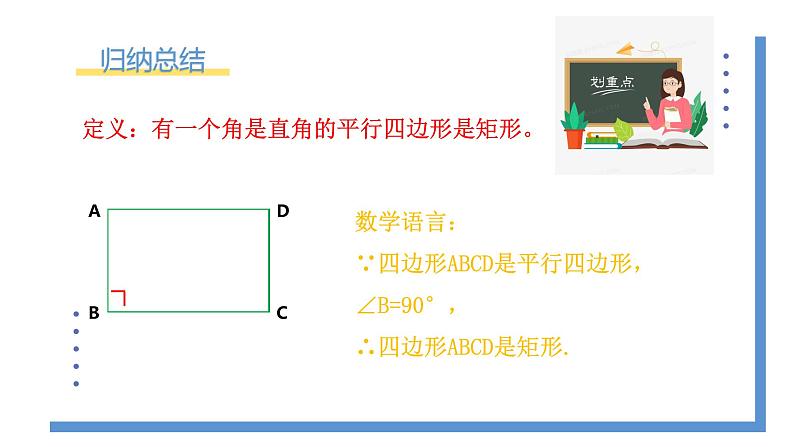
定义：有一个角是直角的平行四边形是矩形。
数学语言：∵四边形ABCD是平行四边形，∠B=90°，∴四边形ABCD是矩形.
问题1：除了定义以外，判定矩形的方法还有没有呢？
矩形是特殊的平行四边形.
类似地，那我们研究矩形的性质的逆命题是否成立.
问题2 上节课我们已经知道“矩形的对角线相等”，反过来，小明猜想对角线相等的四边形是矩形，你觉得对吗？
我猜想：对角线相等的平行四边形是矩形.
不对，等腰梯形的对角线也相等.
不对，矩形是特殊的平行四边形，所以它的对角线不仅相等且平分.
你能帮助小伙伴们证明这一猜想吗？
已知：如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证：□ABCD是矩形.证明：∵AB = DC,BC = CB,AC = DB, ∴ △ABC≌△DCB , ∴∠ABC = ∠DCB. ∵AB∥CD, ∴∠ABC + ∠DCB = 180°, ∴ ∠ABC = 90°, ∴ □ ABCD是矩形（矩形的定义）.
分析：要证明□ABCD是矩形，只要证明其中一个角是直角即可。
矩形的判定定理：对角线相等的平行四边形是矩形.
数学语言：在平行四边形ABCD中，∵AC=BD，∴平行四边形ABCD是矩形.
小颖同学用四步画出了一个四边形，他的画法是“边—直角、边—直角、边—直角、边”，他说这就是一个矩形，他的判断对吗?
想一想：矩形的四个角都是直角，反过来，一个四边形至少有几个角是直角时，这个四边形就是矩形呢？
猜想：一个四边形至少有三个角是直角时，这个四边形就是矩形。
已知：如图,在四边形ABCD中,∠A=∠B=∠C=90°.求证：四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°，∴AD∥BC,AB∥CD.∴四边形ABCD是平行四边形，∴四边形ABCD是矩形.
矩形的判定定理：有三个角是直角的四边形是矩形.
数学语言：在四边形ABCD中，∵ ∠A=∠B=∠C=90°,∴四边形ABCD是矩形.
议一议：你有什么方法检查你家的门框是不是矩形？如果仅有一根较长的绳子，你怎样检查？说明理由.
先检查两组对边是否相等，判断它是否是一个平行四边形；再检查对角线是否相等，判断它是否是一个矩形.
【例2】如图，在□ABCD中，对角线AC与BD相交于点O，△ABO是 等边三角形，AB=4，求□ABCD的面积.
解：∵四边形ABCD是平行四边形，∴OA=OC，OB=OD.又∵△ABO是等边三角形，∴OA=OB=AB=4.∴OA=OC=OB=OD=4.∴AC=BD=2OA=2×4=8.∴□ABCD是矩形，∴∠ABC=90°
在Rt△ABC中，由勾股定理，得AB2+BC2=AC2，
1.下列各句判定矩形的说法是否正确？
（1）对角线相等的四边形是矩形；
（2）对角线互相平分且相等的四边形是矩形；
（3）有一个角是直角的四边形是矩形；
（5）有三个角是直角的四边形是矩形；
（6）四个角都相等的四边形是矩形；
（7）对角线相等，且有一个角是直角的四边形是矩形；
（4）有三个角都相等的四边形是矩形;
（8）一组对角互补的平行四边形是矩形；
2.已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是(　　)A．∠A＝∠B B．∠A＝∠CC．AC＝BD D．AB⊥BC
3.（2022恩施州中考）如图，在四边形ABCD中，∠A＝∠B＝90°，AD＝10cm，BC＝8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是（　　）
A．当t＝4s时，四边形ABMP为矩形B．当t＝5s时，四边形CDPM为平行四边形C．当CD＝PM时，t＝4sD．当CD＝PM时，t＝4s或6s
4.如图，平行四边形ABCD中，对角线AC、BD相交于点O，延长OA到N，使ON＝OB，再延长OC至M，使CM＝AN.求证：四边形NDMB为矩形．
证明：∵四边形ABCD为平行四边形， ∴AO＝OC，OD＝OB.∵AN＝CM，ON＝OB，∴ON＝OM＝OD＝OB，∴四边形NDMB为平行四边形，MN＝BD， ∴平行四边形NDMB为矩形．
判定定理1：有三个角是直角的四边形是矩形
判定定理2：对角线相等的平行四边形是矩形
矩形的定义：有一个角是直角的平行四边形是矩形