广西壮族自治区钦州市浦北县2021-2022学年八年级下学期期末数学试题(word版含答案)

2022年春季学期期末教学质量监测

八年级数学

（考试时间：120分钟；满分120分）

第Ⅰ卷

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1．下列根式中，最简二次根式是（    ）

A． B． C． D．

2．下列各组线段中，可以构成直角三角形的是（    ）

A．2，2，2 B．2，2，4 C．2，3，4 D．5，12，13

3．2022年扬帆中学招聘专任教师，对笔试和面试分别赋权4，6．李明的笔试成绩为90分，面试成绩为80分，那么他的最后成绩是（    ）

A．80分 B．84分 C．86分 D．90分

4．下列运算正确的是（    ）

A．  B．

C．  D．

5．10名同学参加学校组织的书法比赛．已知他们所得的分数互不相同，共设6个获奖名额．小伟知道自己的比赛分数后，要判断自己能否获奖，还需知道这10名同学成绩的统计量是（    ）

A．平均数 B．中位数 C．众数 D．方差

6．下列选项中，y是x的函数的是（    ）

A． B． C． D．

7．如图，下列选项中，不能判断四边形ABCD是平行四边形的是（    ）

A．， B．，

C．， D．，

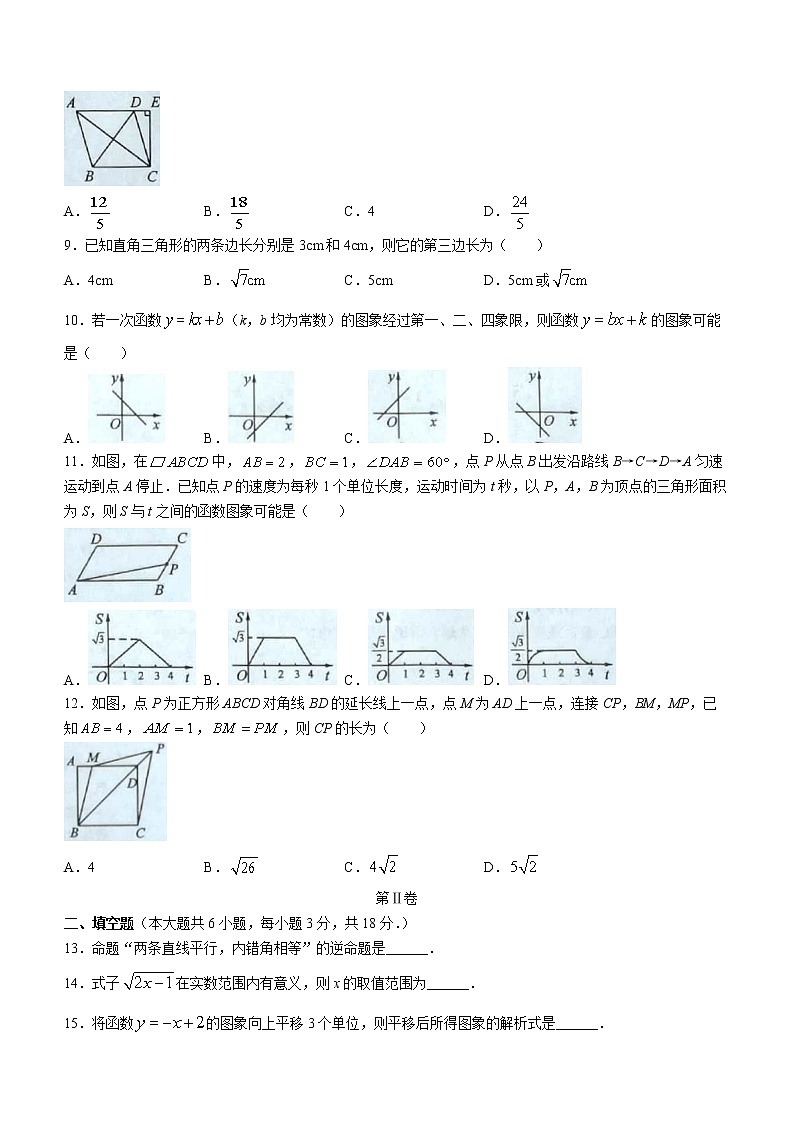
8．如图，在菱形ABCD中，，，过点C作，交AD的延长线于点E，则线段CE的长为（    ）

A． B． C．4 D．

9．已知直角三角形的两条边长分别是3cm和4cm，则它的第三边长为（    ）

A．4cm B． C．5cm D．5cm或

10．若一次函数（k，b均为常数）的图象经过第一、二、四象限，则函数的图象可能是（    ）

A． B． C． D．

11．如图，在中，，，，点P从点B出发沿路线B→C→D→A匀速运动到点A停止．已知点P的速度为每秒1个单位长度，运动时间为t秒，以P，A，B为顶点的三角形面积为S，则S与t之间的函数图象可能是（    ）

A． B． C． D．

12．如图，点P为正方形ABCD对角线BD的延长线上一点，点M为AD上一点，连接CP，BM，MP，已知，，，则CP的长为（    ）

A．4 B． C． D．

第Ⅱ卷

二、填空题（本大题共6小题，每小题3分，共18分．）

13．命题“两条直线平行，内错角相等”的逆命题是______．

14．式子在实数范围内有意义，则x的取值范围为______．

15．将函数的图象向上平移3个单位，则平移后所得图象的解析式是______．

16．如图是甲、乙两人6次定点投篮测试（每次投篮10个）成绩的统计图，甲、乙两人测试成绩的方差分别记作、，则______（填“＞”，“＜”或“=”）．

17．如图，在矩形ABCD中，点E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，若，，则FD的长为______．

18．在平面直角坐标系中，若一个正比例函数的图象经过，两点，则m，n满足的数量关系为______．

三、解答题（本大题共7小题，共66分．解答应写出文字说明、证明过程或演算步骤，）

19．（本题满分8分，每小题4分）计算：

（1）； （2）．

20．（本题满分8分）已知，，求下列各式的值．

（1）；

（2）．

21．（本题满分10分）如图，在△ABC中，，，，．

（1）求△ABC的周长；

（2）△ABC是否是直角三角形？请说明理由？

22．（本题满分10分）读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．阳光中学为了解该校八年级500名学生的课外阅读情况，随机抽样调查了20名学生每周用于课外阅读的时间（单位：min），过程如下：

收集数据：

30 60 81 50 44 110 130 146 80 100

60 80 120 140 75 81 10 30 81 92

整理数据：

分析数据：

请根据以上信息，解答下列问题：

（1）写出表格中的数据：______，______，______；

（2）请用样本中的统计量估计该校八年级学生每周用于课外阅读时间的等级为______．

（3）请估计该校八年级学生等级为“B”的人数；

（4）假设平均阅读一本课外书的时间为320min，请你选择合适的样本统计量估计该校学生每人一年（按52周计算）平均阅读多少本课外书．

23．（本题满分10分）如图，已知直线交x轴于点A，交y轴于点B，直线交x轴于点D，与直线AB相交于点．

（1）根据图象信息，写出关于x的不等式的解集；

（2）若点A的坐标为，求直线AB的解析式；

（3）在（2）的条件下，求四边形BODC的面积．

24．（本题满分10分）一列快车从A地驶往B地，一列慢车从B地驶往A地，两车同时出发，图中的折线表示两车之间的距离与慢车行驶时间之间的函数关系图象，请根据提供的信息解答下列问题：

（1）快车的速度是______；

（2）请求出线段BC的函数关系式；

（3）若第一列快车与慢车相遇时，第二列快车从B地出发驶往A地，速度与第一列快车相同，请问第二列快车出发多长时间与慢车相距200km？

25．（本题满分10分）

【了解概念】

定义：画出四边形的任何一边所在直线，整个四边形都在这条直线的同一侧，这样的四边形叫做凸四边形；

两条对角线相等的凸四边形叫做等线四边形，两条对角线所夹锐角为60°的等线四边形叫做强等线四边形．

【理解运用】

（1）下列四边形中，一定是等线四边形的是______（填序号即可）．

①平行四边形；②矩形；③菱形；④正方形．

【拓展提升】

（2）如图，在△ABC中，，分别以AC，AB为边向△ACB外作菱形ACFG和菱形ABDE，且，连接CG，BE，GE．

①求证：四边形BCGE是强等线四边形；

②若，，P，Q分别是BC，GE的中点，连接PQ，直接写出PQ的长．

2022年春季学期期末教学质量监测参考答案

八年级  数学

一、选择题（本大题共12小题，每小题3分，共36分．）

二、填空题（本大题共6小题，每小题3分，共18分．）

13．内错角相等，两条直线平等 14．

15． 16． 17．4 18．

三、解答题（本大题共7小题，共66分．）

19．（本题满分8分，每小题4分）

解：（1）原式．

（2）原式．

20．（本题满分8分）

解：（1）当，时，

原式

．

（2）当，时，

原式

．

21．（本题满分10分）

解：（1）∵，，，

∴．

同理，．

∴的周长为．

（2）∵，

，，∴．∴不是直角三角形．

22．（本题满分10分）

解：（1）5，4，80.5．

（2）B．

（3）（人），

∴估计该校八年级等级为“B”的学生有200人．

（4）由题意得，选择样本的平均数估计该校学生每人一年平均阅读课外书数量，（本），

∴估计该校学生每人一年（按52周计算）平均阅读课外书是13本．

23．（本题满分10分）

解：（1）根据图象可得，关于x的不等式的解集为．

（2）∵直线AB过点，，∴  解得

∴直线AB的解析式为．

（3）∵直线AB交y轴于点B，

∴当时，．∴B点坐标为．

又∵直线交x轴于点D，∴当时，．

∴D点坐标为．∴．

∴．

24．（本题满分10分）

解：（1）160．

（2）由图象可知，A，B两地之间的距离是960km，当慢车行驶6h时，快车到达B地，而D点表示慢车需行驶12h达到A地．

∴快车的速度是：.

∴慢车的速度是：．

又∵两车行驶960km相遇，所用时间为，∴点B的坐标为．

∴两车相遇2h后，两车相距，

∴点C的坐标为．

设线段BC的函数关系式为，把，代入得

解得

∴线段BC的函数关系式为，．

（3）①设第二列快车出发a h，快车还未追上慢车，与慢车相距200km，

，解得．

即第二列快车出发1.5h，与慢车相距200km.

②第二列快车追上慢车以后再超过慢车，与慢车相距200km.

设第二列快车出发ah，与慢车相距200km，

则,解得，（舍去）．

综上所述，第二列快车出发1.5h，与慢车相距200km．

25.（本题满分10分）

解：（1）②，④．

（2）①如图，连接BG，CE交于点M, CE交AB于点N，

∵，∴．

即．

∵四边形ACFG和ABDE均为菱形，∴，．

∴．

∴，．∴四边形BCGE是等线四边形．

∵，，

∴．∴四边形BCGE是强等线四边形．

②．