

2021-2022学年广东省惠州市高一(下)期末数学试卷(Word解析版)
展开2021-2022学年广东省惠州市高一(下)期末数学试卷
题号 | 一 | 二 | 三 | 四 | 总分 |
得分 |
|
|
|
|
|
一、单选题(本大题共8小题,共40分)
- 已知复数满足其中为虚数单位,则的虚部是( )
A. B. C. D.
- 已知向量,共线,则的值为( )
A. B. C. D.
- 小红、小明、小芳参加技能展示比赛,他们约定用“石头、剪子、布”的方式确定出场的先后顺序.问在个回合中个人都出“布”的概率是( )
A. B. C. D.
- 已知某地区中小学生人数和近视情况分别如下图所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量和估计抽取的高中生近视人数分别为.( )
A. , B. , C. , D. ,
- 在中,,则( )
A. B. C. D.
- 一个直角三角形的两条直角边长分别为和,将该三角形绕其斜边旋转一周得到的几何体的表面积为( )
A. B. C. D.
- 已知甲、乙两个企业生产同一款产品的合格率分别为和,通过市场调查发现甲、乙两企业产品的市场占有率分别为和现从市场上随机购买一件该产品,则买到的产品是合格品的概率为( )
A. B. C. D.
- 某校为调查高一年级的某次考试的数学成绩情况,随机调查高一年级甲班名学生,成绩的平均数为,方差为,乙班名学生,成绩的平均数为,方差为,则这名学生成绩的平均数和方差分别为( )
A. , B. , C. , D. ,
二、多选题(本大题共4小题,共20分)
- 有甲、乙两种报纸供市民订阅,记事件“只订甲报纸”,事件“至少订一种报纸”,事件“至多订一种报纸”,事件“不订甲报纸”,事件“一种报纸也不订”下列命题正确的是( )
A. 与是互斥事件 B. 与是互斥事件,且是对立事件
C. 与不是互斥事件 D. 与是互斥事件
- 已知圆锥的底面半径为,高为,为顶点,,为底面圆周上两个动点,则( )
A. 圆锥的体积为
B. 圆锥的侧面展开图的圆心角大小为
C. 圆锥截面的面积的最大值为
D. 从点出发绕圆锥侧面一周回到点的无弹性细绳的最短长度为
- 将一组数据从小到大排列为:,,,,中位数和平均数均为,方差为,从中去掉第项,从小到大排列为:,,,,方差为,则下列说法中正确的是( )
A. B. ,,,的中位数为
C. ,,,的平均数为 D.
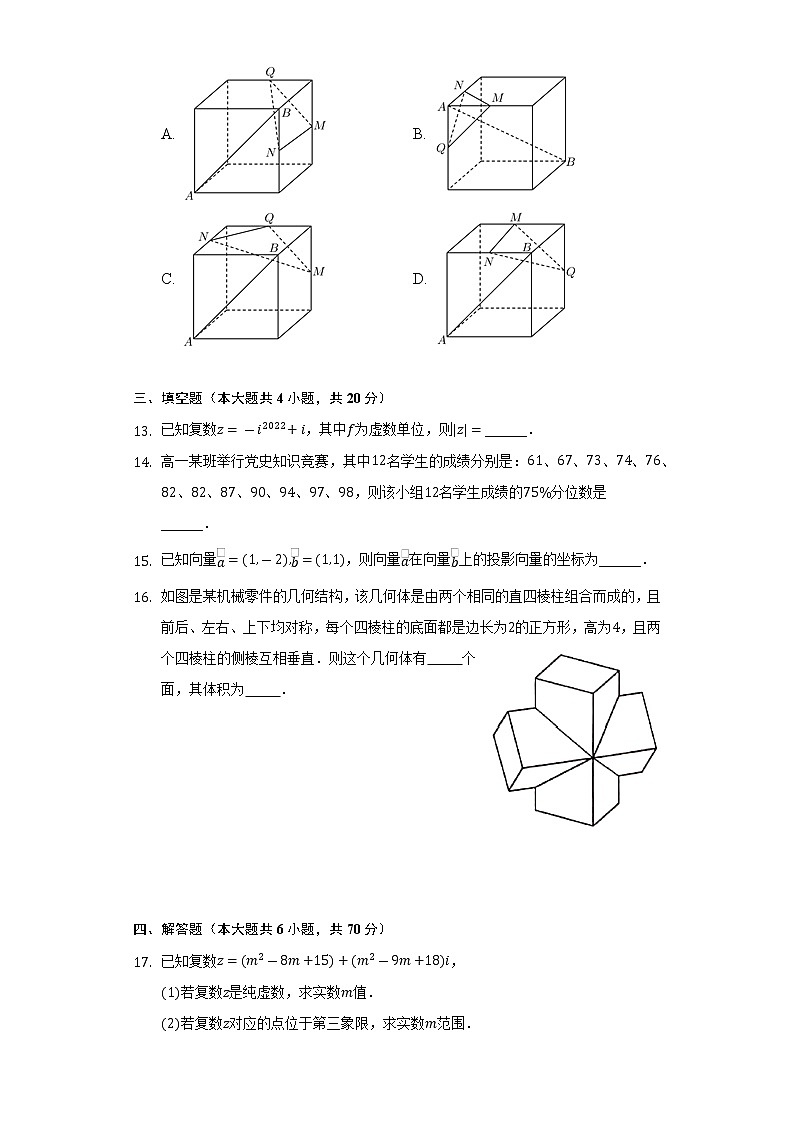
- 如图,在下列四个正方体中,,为正方体的两个顶点,,,为所在棱的中点,则在这四个正方体中,直线与平面垂直的是( )
A. B.
C. D.
三、填空题(本大题共4小题,共20分)
- 已知复数,其中为虚数单位,则______.
- 高一某班举行党史知识竞赛,其中名学生的成绩分别是:、、、、、、、、、、、,则该小组名学生成绩的分位数是______.
- 已知向量,则向量在向量上的投影向量的坐标为______.
- 如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为的正方形,高为,且两个四棱柱的侧棱互相垂直.则这个几何体有 个面,其体积为 .
四、解答题(本大题共6小题,共70分)
- 已知复数,
若复数是纯虚数,求实数值.
若复数对应的点位于第三象限,求实数范围. - 已知向量,,.
若点,,能构成三角形,求实数应满足的条件;
若为直角三角形,且为直角,求实数的值. - 年月开始,新冠奥密克戎病毒在上海等地肆虐,感染病毒人数急剧上升.全国各地积极应对,认真做好新冠病毒防控工作,实现社会面动态清零.为保障抗疫一线医疗物资的供应,惠州市某企业加班加点生产口罩、防护服,消毒水等防疫物品.在加大生产的同时,该公可狠抓质量管理,不定时抽查口罩质量.该企业质检人员从所生产的口罩中随机抽取了个,将其质量指标值分成以下六组:,,,,得到如图所示的频率分布直方图.
求出直方图中的值;
利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数.中位数精确到
- 在,这两个条件中任选一个,补充在下面问题中,并给出解答.
问题:在中,角,,的对边分别为,,,________.
求;
,,求的边上的中线的长. - 如图,在中,,,,,分别是,上的点,且,将沿折起到的位置,使,如图.
求证:平面;
若,为的中点,作出过且与平面平行的截面,并给出证明;
当点在何处时,的长度最小,并求出最小值. - 为普及抗疫知识、弘扬抗疫精神,某学校组织防疫知识挑战赛.每位选手挑战时,主持人用电脑出题的方式,从题库中随机出道题,编号为,,,电脑依次出题,选手按规则作答,挑战规则如下:
选手每答对一道题目得分,每答错一道题目扣分;
选手若答对第题,则继续作答第题;选手若答错第题,则失去第题的答题机会,从第题开始继续答题;直到道题目出完,挑战结束;
选手初始分为分,若挑战结束后,累计得分不低于分,则选手挑战成功,否则挑战失败.选手甲即将参与挑战,已知选手甲答对题库中任何一题的概率均为,各次作答结果相互独立,且他不会主动放弃任何一次作答机会,求:
挑战结束时,选手甲共答对道题的概率;
挑战结束时,选手甲恰好作答了道题的概率;
选手甲闯关成功的概率.
答案和解析
1.【答案】
【解析】解:,
的虚部是.
故选:.
根据已知条件,结合复数的四则运算,以及虚部的定义,即可求解.
本题主要考查复数的四则运算,以及虚部的定义,属于基础题.
2.【答案】
【解析】解:向量,共线,
,即.
故选:.
直接利用向量共线的坐标运算列式求解值.
本题考查向量共线的坐标运算,是基础题.
3.【答案】
【解析】解:小红、小明、小芳参加技能展示比赛,
他们约定用“石头、剪子、布”的方式确定出场的先后顺序.
三个人各自出“布”的概率为,
在个回合中个人都出“布”的概率是:
.
故选:.
先求出三个人各自出“布”的概率,再根据相互独立事件概率乘法公式能求出结果.
本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
4.【答案】
【解析】
【分析】
本题考查样本容量、频数的求法,考查扇形统计图、条形图的性质等基础知识,考查运算求解能力,属于基础题.
利用总量乘以抽取比例即可得到样本容量,根据图表可知高中生近视率,由此能估计抽取的高中生近视人数.
【解答】
解:所有的学生数为,样本容量为,
根据甲图以及抽取百分比可知样本中高中生人数为,
根据乙图可知抽取的高中生近视人数为.
故选:.
5.【答案】
【解析】解:因为,
则.
故选:.
由已知结合向量的线性表示即可求解.
本题主要考查了向量的线性表示,属于基础题.
6.【答案】
【解析】解:如图所示,
在直角中,,
可得,可得,
即旋转体的底面圆的半径为,
所以该旋转体的表面积为:
,
故选:.
根据题意,结合圆锥的侧面积公式,准确运算,即可求解.
本题考查了几何体的表面积的计算,属于基础题.
7.【答案】
【解析】解:买到的产品是合格品的概率为.
故选:.
利用相互独立事件概率乘法公式求解.
本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式的灵活运用.
8.【答案】
【解析】解:设这名学生成绩的平均数为,方差为,
高一年级甲班名学生,成绩的平均数为,方差为,乙班名学生,成绩的平均数为,方差为,
,.
故选:.
根据已知条件,运用平均数公式和方差公式,即可求解.
本题考查了平均数公式和方差公式的应用,需要学生熟练掌握公式,属于基础题.
9.【答案】
【解析】解:对于,事件,有可能同时发生,不是互斥事件,故A错误;
对于,事件与不可能同时发生,且发生的概率之和为,是互斥事件,且为对立事件,故B正确;
对于,事件与有可能同时发生,不是互斥事件,故C正确;
对于,事件与有可能同时发生,不是互斥事件,故D错误.
故选:.
利用互斥事件、对立事件的定义直接求解.
本题考查互斥事件、对立事件的定义等基础知识,是基础题.
10.【答案】
【解析】解:对于:因为圆锥的底面半径为,高为,所以体积,故A正确;
对于:设圆锥的母线为,则,
设圆锥的侧面展开图的圆心角为,由弧长公式得:,即,解得:,故B错误;
对于:显然当圆锥截面为轴截面时,其面积最大,此时,故C正确;
对于:由可得该圆锥的侧面展开图是半径为的半圆,
所以从点出发绕圆锥侧面一周回到点的无弹性细绳的最短长度为,故D错误;
故选:.
对于:直接求出圆锥的体积即可判断;对于:直接求出圆锥的侧面展开图的圆心角即可判断;对于:先判断出圆锥截面为轴截面时,其面积最大,然后可判断;对于:利用圆锥的侧面展开图可求解判断.
本题考查了立体几何的综合应用,属于中档题.
11.【答案】
【解析】解:,,,,中位数和平均数均为,
,,故A正确;
,,,的中位数为,
不一定等于,,,,的中位数不一定为,故B错误;
,,,,的平均数为,故C正确;
,,
,
,
,故D错误.
故选:.
由中位数的定义即可判断,;由平均数定义判断;由方差定义判断.
本题考查命题真假的判断,考查平均数、中位数、方差等基础知识,考查运算求解能力,是基础题.
12.【答案】
【解析】解:对于选项,如图,因为,,为所在棱的中点,故由正方体的性质易得,,,,所以,,由于,故AB平面,故A选项正确;
对于选项,如图,因为,,为所在棱的中点,所以,,由正方体的性质得,,,所以平面,故CD,所以,同理得,,故AB平面,故B选项正确;
对于选项,如图,因为,,为所在棱的中点,所以,,所以在中,与夹角为,故异面直线与所成的角为,故AB平面不成立,故C选项错误;
对于选项,同选项,可判断平面,故D选项正确;
故选:.
根据正方体的性质,结合线面垂直的判定定理依次讨论各选项即可得答案.
本题考查了线面垂直的判定定理,属于中档题.
13.【答案】
【解析】解:由题意可得,
即,
故答案为:.
由复数的运算可得,再根据复数的模长公式求解即可.
本题考查了复数的运算,复数的模,是基础题.
14.【答案】
【解析】解:因为,
所以该小组名学生成绩的分位数是,
故答案为:.
因为,所以所求的即为与的平均值.
本题考查了百分位数的求解,考查了学生的运算能力,属于基础题.
15.【答案】
【解析】解:由题可知,向量在向量上的投影向量为
,
故答案为:.
根据投影向量的定义,代入数据,即可求得答案.
本题主要考查投影向量,属于基础题.
16.【答案】
【解析】
【分析】
本题考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力能力与运算求解能力,是中档题.
直接由对称性可得该几何体面的个数;该几何体的体积为两个四棱柱的体积和减去两个四棱柱交叉部分的体积,两个四棱柱的体积和为,交叉部分的体积为四棱锥的体积的倍,由该几何体前后、左右、上下均对称,知四边形为边长为的棱形,设的中点为,连结,,由题意得为四棱锥的高,求出四棱锥的体积,由此能求出这个几何体的体积.
【解答】
解:由对称性可知,该几何体共有个面;
该几何体的直观图如图所示,
该几何体的体积为两个四棱柱的体积和减去两个四棱柱交叉部分的体积,
两个四棱柱的体积和为:,
交叉部分的体积为四棱锥的体积的倍,
在等腰中,,边上的高为,则,
由该几何体前后、左右、上下均对称,知四边形为边长为的棱形,
设的中点为,连结,,由题意得为四棱锥的高,
在中,,
又,
,
,,
这个几何体的体积为.
故答案为:.
17.【答案】解:复数是纯虚数,
,解得.
复数对应的点位于第三象限,
,解得.
实数范围是.
【解析】本题考查了纯虚数和复数的几何意义,属于基础题.
由于复数是纯虚数,可得,解得即可.
由于复数对应的点位于第三象限,可得,解得的取值范围即可.
18.【答案】解:若点,,能构成三角形,则这三点不共线,即与不共线,
由,,
知,
解得,满足条件;
若根据点、、能构成三角形,必须任意两边长的和大于第三边的长,
即由去解答,相应给分
若为直角三角形,且为直角,则,
,
即,
解得.
【解析】根据点,,能构成三角形知这三点不共线,
即与不共线,由此求出满足的条件;
根据为直角三角形得出,
列方程求出的值.
本题考查了平面向量的坐标表示与运算问题,是基础题.
19.【答案】解:由频率分布直方图可得,
解得;
平均数为.
因为,,
所以中位数位于之间,
设中位数为,则,解得,
所以可以估计该企业所生产口罩的质量指标值的平均数为,中位数为;
【解析】根据频率分布直方图中所有小矩形的面积之和为得到方程,解得即可;
根据频率分布直方图中平均数、中位数计算公式计算可得;
本题考查了频率分布直方图中相关计算问题,属于基础题.
20.【答案】解:若选,即,得,
,或,
,;
若选:,
由正弦定理,得,
,,,;
是的边上的中线,,
,
,.
【解析】若选,由已知可得,可求出,进而求出;
若选:由正弦定理,得,可求出,进而求出;
是的边上的中线,,利用向量法可求的长.
本题考查正余弦定理,以及向量法求边长,属中档题.
21.【答案】解:证明:在 中,,,
所以 ,所以 .
又 ,,所以 面,
由 面,所以 .
又 ,,所以 面.
解:如图,过点作交于,过作交于,
过点作交于,连接,则平面平面.
证明如下:,,且,
,,,,四点共面.
,平面,平面,
平面,同理平面
又,平面,平面,
平面平面.
解:设 ,则 ,连接 ,
在 中,,
由知 面,
故 ,故 .
当 时, 有最小值 ,故 长度的最小值为 ,
此时 ,即 为 的中点.
【解析】推导出,从而面,进而又 ,由此能证明 面.
过点作交于,过作交于,过点作交于,连接,推导出,从而,,,四点共面,推导出平面,平面,由此能证明平面平面.
设 ,则 ,连接 ,则,由 面,知,故 由此能求出 长度的最小值为 , 为 的中点.
本题考查线面垂直的证明,考查与平面平行的截面的确定,考查线段长的最小值的求法及点的位置的确定,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
22.【答案】解:设为选手答对题,其中,,
设挑战结束后,选手甲共答对道题为事件,
选手甲共答对道即选手甲前题答对且第题答错,
由事件独立性的定义得.
设挑战结束时,选手甲恰好作答了道题为事件,
选手甲恰好作答了道题即选手甲第一题答错或第一题答对且第题答错,
,
由概率的加法公式和事件独立性的定义得.
设选手甲挑战成功为事件,
若选手甲挑战成功,则选手甲共作答了道题,且选手甲只可能作答题或道题,
“选手甲闯关成功”是“选手甲恰好作答了道题”的对立事件,
根据对立事件的性质得.
【解析】设为选手答对题,其中,,,设挑战结束后,选手甲共答对道题为事件,选手甲共答对道,即选手甲前题答对且第题答错,可得,再结合相互独立事件概率乘法公式,即可求解.
设挑战结束时,选手甲恰好作答了道题为事件,选手甲恰好作答了道题即选手甲第一题答错或第一题答对且第题答错,即,结合概率的加法公式和事件独立性的定义,即可求解.
设选手甲挑战成功为事件,若选手甲挑战成功,则选手甲共作答了道题,且选手甲只可能作答题或道题,“选手甲闯关成功”是“选手甲恰好作答了道题”的对立事件,结合对立事件的性质,即可求解.
本题考查概率的求法,以及考查相互独立事件概率乘法公式和互斥事件概率加法公式,属于基础题.
2021-2022学年广东省广州市三校联考高一(下)期末数学试卷(Word解析版): 这是一份2021-2022学年广东省广州市三校联考高一(下)期末数学试卷(Word解析版),共21页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年广东省肇庆市高一(下)期末数学试卷(Word解析版): 这是一份2021-2022学年广东省肇庆市高一(下)期末数学试卷(Word解析版),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年广东省湛江市高二(下)期末数学试卷(Word解析版): 这是一份2021-2022学年广东省湛江市高二(下)期末数学试卷(Word解析版),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












