专题12 集合的基本运算（补集与集合的综合应该运算）-暑假初三升高一数学衔接知识自学讲义（人教A版2019）

这是一份专题12 集合的基本运算（补集与集合的综合应该运算）-暑假初三升高一数学衔接知识自学讲义（人教A版2019），文件包含专题12集合的基本运算补集与集合的综合应该运算解析版docx、专题12集合的基本运算补集与集合的综合应该运算原卷版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

专题12 集合的基本运算（补集与集合的综合应该运算）
【知识点梳理】
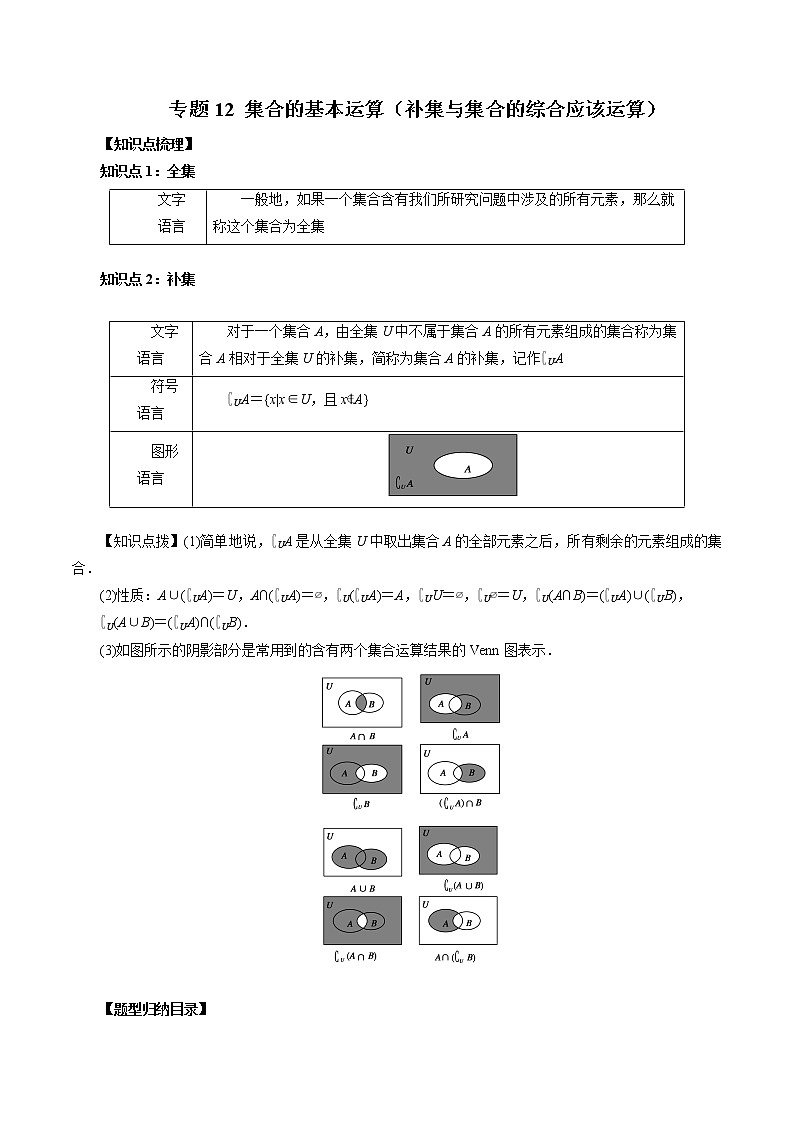
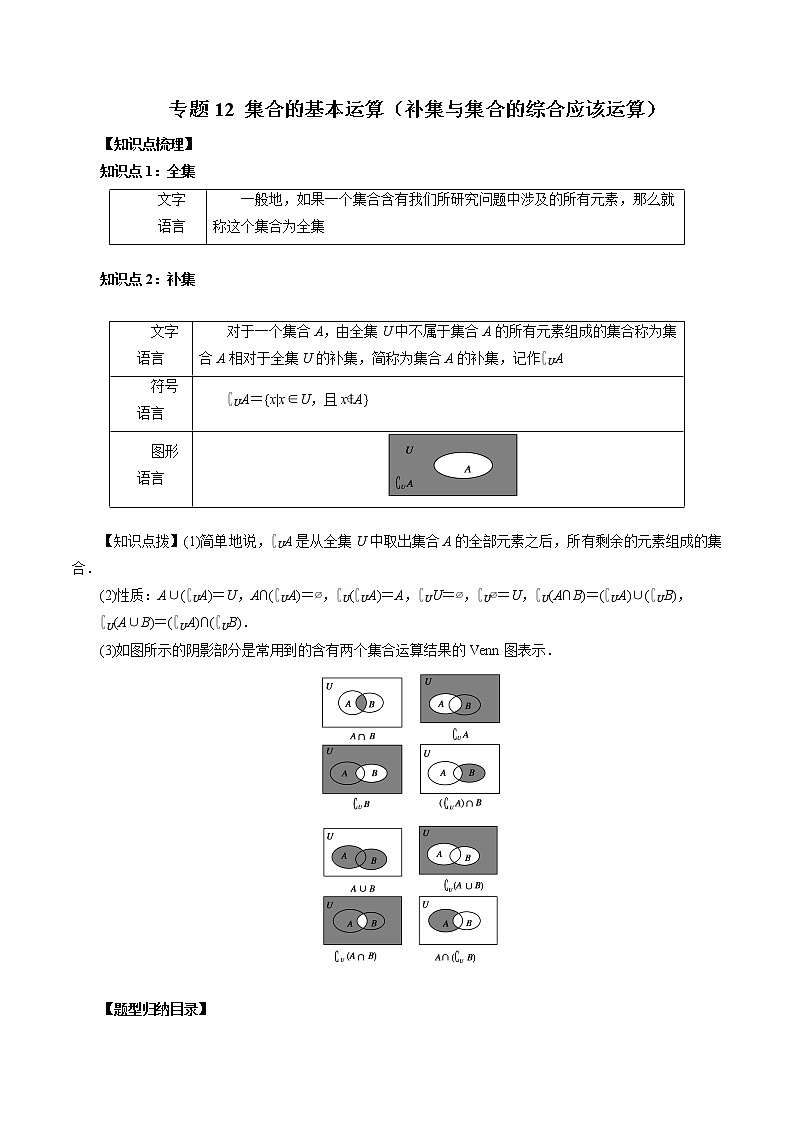
知识点1：全集
文字
语言
一般地，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集

知识点2：补集

文字语言
对于一个集合A，由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集，简称为集合A的补集，记作∁UA
符号语言
∁UA＝{x|x∈U，且x∉A}
图形语言


【知识点拨】(1)简单地说，∁UA是从全集U中取出集合A的全部元素之后，所有剩余的元素组成的集合．
(2)性质：A∪(∁UA)＝U，A∩(∁UA)＝∅，∁U(∁UA)＝A，∁UU＝∅，∁U∅＝U，∁U(A∩B)＝(∁UA)∪(∁UB)，
∁U(A∪B)＝(∁UA)∩(∁UB)．
(3)如图所示的阴影部分是常用到的含有两个集合运算结果的Venn图表示．



【题型归纳目录】
题型1：补集的运算
题型2：集合的交并、补集的综合运算
题型3：与补集有关的求参数问题

【典型例题】
题型1：补集的运算
1．（2022·辽宁朝阳·高一阶段练习）如图，已知集合A={-8，1}，B={-8，-5，0，1，3}，则Venn图中阴影部分表示的集合为（       ）

A．{-5，0，3} B．{-5，1，3}
C．{0，3} D．{1，3}
【答案】A
【解析】
【分析】
由已知，结合给出的Venn图可判断阴影部分为∁BA, 根据给到的集合和集合，可直接进行求解.
【详解】
因为集合A={-8，1}，B={-8，-5，0，1，3}，
Venn图中阴影部分表示的集合为∁BA={-5，0，3}．
故选：A.
2．（2022·广东·化州市第三中学高一阶段练习）若全集，且，则集合 （       ）
A．{1，4} B．{0，4} C．{2，4} D．{0，2}
【答案】B
【解析】
【分析】
根据补集的定义求解即可.
【详解】
解：因为全集，且，
所以.
故选：B
3．（2022·四川·宁南中学高一阶段练习（理））已知集合，集合，则（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
直接求出.
【详解】
因为集合，集合，所以.
故选：C.
4．（2022·陕西渭南·高一期末）若全集，且，则（       ）
A．或 B．或
C． D．或.
【答案】D
【解析】
【分析】
根据集合补集的概念及运算，准确计算，即可求解.
【详解】
由题意，全集，且，
根据集合补集的概念及运算，可得或.
故选：D.
5．（2022·河南平顶山·高一期末）已知集合，，则（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
先化简集合，进而求得集合A，B的补集，再逐项判断.
【详解】
因为集合，
所以或，
因为，
所以，
所以，
故选：D
6．（2022·浙江省定海第一中学高一开学考试）已知全集，集合，则（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
直接利用补集的定义即可求得.
【详解】
因为全集，集合，
所以.
故选：D
7．（2022·河南·林州一中高一开学考试）已知全集，集合，则（       ）
A． B．或
C．或 D．
【答案】D
【解析】
【分析】
直接根据补集的概念求解即可.
【详解】
解：因为全集，集合，
所以
故选：D
题型2：集合的交并、补集的综合运算
1．（2022·江苏·无锡市市北高级中学高一期中）已知全集为，集合，集合，则（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
利用题意首先求得补集，然后进行交集运算即可求得最终结果.
【详解】
集合，4，，集合，，
由补集的定义可得：，，，
然后进行交集运算可得：.
故选：C.
2．（2022·江苏·海安市曲塘中学高一期中）设全集，，，则（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
根据补集的概念求出，再根据并集运算即可求出结果.
【详解】
由题意可知，又，所以.
故选:A.
3．（2022·河北省唐县第一中学高一阶段练习）设全集，集合，，则（       ）
A． B． C． D．
【答案】B
【解析】
【分析】
根据补集、交集的定义计算可得；
【详解】
解：因为，所以，又；
所以；
故选：B
4．（2022·四川攀枝花·高一期末）设全集，集合，，则图中阴影部分表示的集合是（       ）

A． B． C． D．
【答案】B
【解析】
【分析】
由图中阴影部分可知对应集合为，然后根据集合的基本运算求解即可.
【详解】
解：由图中阴影部分可知对应集合为

全集，2，3，4，，集合，，，3，，
=，=．
故选：．
5．（2022·全国·高一课时练习）设集合 ，，，若全集，则下列结论正确的是（　　）
A．
B．
C．
D．
【答案】D
【解析】
【分析】
根据集合，，的关系求解即可.
【详解】
集合，，的关系如下图，

由图可知只有正确．
故选：D.
6．（2022·重庆八中高一期末）设全集为，集合，，则（       ）
A． B． C． D．
【答案】B
【解析】
【分析】
先求出集合B的补集，再根据集合的交集运算求得答案.
【详解】
因为，所以，
故，
故选:B.
7．（2022·天津·油田三中高一阶段练习）已知全集，，，则______．
【答案】
【解析】
【分析】
先求集合A的补集，再求A的补集与集合B的交集即可.
【详解】
由得，
又，则
故答案为：
8．（2022·全国·高一课时练习）设，，全集，， 或，则______.
【答案】1
【解析】
【分析】
根据补集的概念对应系数相等即可求出结果.
【详解】
因为，，所以或.
又或，所以，，所以.
故答案为：1.
9．（2022·上海南汇中学高一阶段练习）设全集，若，，，则A=______.
【答案】
【解析】
【分析】
写出全集U，作出韦恩图，将全集U中的元素放置在合适的区域内即可求出集合A.
【详解】
依题意，全集，作出韦恩图，如下图所示：

观察韦恩图知集合.
故答案为：
10．（2022·广东·佛山市南海区狮山高级中学高一阶段练习）某城市数，理，化竞赛时，高一某班有24名学生参加数学竞赛，28名学生参加物理竞赛，19名学生参加化学竞赛，其中参加数，理，化三科竞赛的有7名，只参加数，物两科的有5名，只参加物，化两科的有3名，只参加数，化两科的有4名．若该班学生共有48名，问没有参加任何一科竞赛的学生有__名．
【答案】3
【解析】
【分析】
根据题意画出图形，根据图形求出单独参加数理化的人数，然后把单独参加数理化的人数和参加2门，3门竞赛的人数加在一起 ，即可得到竞赛的总人数，然后即可求出没有参加任何一科竞赛的学生人数.
【详解】
画三个圆分别代表参加数学，物理，化学的人．
因为参加数，理，化三科竞赛的有7名，只参加数，物两科的有5名，只参加物，化两科的有3名，只参加数，化两科的有4名．分别填入图形中，
又因为有24名学生参加数学竞赛，28名学生参加物理竞赛，19名学生参加化学竞赛，
故单独参加数学的有8人，单独参加物理的有13人，单独参加化学的有5人，
故是参加竞赛的人数，所以没参加的人数为人．

故答案为：3．
题型3：与补集有关的求参数问题
1．（2022·四川省蒲江县蒲江中学高一阶段练习）已知集合，集合，若则实数的取值范围是______．
【答案】或
【解析】
【分析】
首先分别化简集合,计算出，根据即可计算出实数的取值范围.
【详解】
由题意得：

所以
因为
所以或
即或
故答案为：或
2．（2022·广西·玉林市第十一中学高一阶段练习）设全集，，，则a=____________．
【答案】或2
【解析】
【分析】
根据补集的运算法则，得到，求出的值，检验得出最后结果.
【详解】
因为，，所以，因为，所以，解得：或，经检验，均符合要求.
故答案为：或2
3．（2022·辽宁·渤海大学附属高级中学高一阶段练习）已知全集，集合，集合，，则实数的取值范围是______.
【答案】或
【解析】
【分析】
解一元二次不等式得集合，求出其补集，根据集合间的关系列出的不等式解出即可.
【详解】
或，
，
又，，
或，或，
故答案为：或.
4．（2022·安徽宿州·高一期中）设集合，，.
(1)求.
(2)若，求实数的取值范围．
【答案】(1)
(2)
【解析】
【分析】
（1）先解出集合，再计算即可；
（2）由得，再按照两根的大小分类讨论解不等式即可.
(1)
，，则；
(2)
，由得，
①当时，即时，，只需，即；
②当时，即时，，满足条件；
③当时，即时，，只需，即；
综上可得：的取值范围是.
5．（2022·河北沧州·高一期末）已知集合，.
(1)当时，求；
(2)若，求实数的取值范围.
【答案】(1)；
(2).
【解析】
【分析】
(1)求出集合A和B，根据并集的计算方法计算即可；
(2)求出，分B为空集和不为空集讨论即可.
(1)
，
当时，，
∴；
(2)
{或x＞4}，
当时，，，解得a＜1；
当时，若，则解得.
综上，实数的取值范围为.
6．（2022·北京·高一期末）已知集合，．
(1)求集合；
(2)当时，求；
(3)若，求的取值范围．
【答案】(1)或
(2)
(3)
【解析】
【分析】
（1）根据题干条件以及补集的定义可得解；
（2）根据题干条件以及交集的定义可得解；
（3）根据（1）可得或，结合，分析即得解
(1)
由题意，
故或
(2)
当时，
故
(3)
由（1）或

若，则
解得
7．（2022·山东临沂·高一期末）已知集合，.
(1)若，求；
(2)求实数的取值范围，使___________成立.
从①，②，③中选择一个填入横线处求解.
注：如果选择多个条件分别解答，按第一个解答计分.
【解析】
(1)，
，
当时，，所以；
(2)由(1)知，，，
所以或，或，
若选①，，则或，
解得或，所以的取值范围为或；
若选②，，则或，
解得或，所以的取值范围为或；
若选③，，则，
解得，所以的取值范围为.

【过关测试】
一、单选题
1．（2022·湖南·高一阶段练习）设集合，，则（       ）
A． B．
C． D．
【答案】C
【解析】
【分析】
解一元二次不等式可求得，根据集合的交集运算即可求得答案.
【详解】
由题意得，
∴，
故选：C
2．（2022·河南·永城市苗桥乡重点中学高一期末）已知集合，，则（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
利用补集定义求出，利用交集定义能求出．
【详解】
解：集合，，
则或，
．
故选：D
3．（2022·云南·昭通市第一中学高一阶段练习）已知集合，，则如图所示的阴影部分表示的集合为（       ）

A． B． C． D．
【答案】B
【解析】
【分析】
利用韦恩图结合集合的基本运算求解.
【详解】
解：因为，，
所以阴影部分表示的集合为.
故选：B.
4．（2022·重庆复旦中学高一开学考试）若集合，，则（       ）．
A． B． C． D．
【答案】A
【解析】
【分析】
根据补集的定义和运算求出，结合交集的概念和运算即可得出结果.
【详解】
由题意知，
，又，
所以.
故选：A
5．（2022·天津天津·高一期末）设全集，集合，则（       ）
A．{3，5} B．{2，4}
C．{1，2，3，4，5} D．{2，3，4，5，6}
【答案】D
【解析】
【分析】
先求补集，再求并集.
【详解】
，则.
故选：D
6．（2022·河北邢台·高一阶段练习）已知集合，则（       ）
A． B． C． D．
【答案】B
【解析】
【分析】
按照并集和补集计算即可.
【详解】
由题意得，，所以．
故选：B.
7．（2022·湖北·宜昌市一中高一阶段练习）若全集，，，则集合（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
计算，，再计算交集得到答案.
【详解】
，，.
故选：D.
8．（2022·江苏·高一专题练习）已知全集，集合，若的元素的个数为4，则的取值范围为（ ）
A． B． C． D．
【答案】A
【解析】
【分析】
根据集合补集的结果个数，即可容易求得参数范围.
【详解】
若的元素的个数为4，则
故选：A.
【点睛】
本题考查由集合的补集元素个数求参数范围，属基础题.
二、多选题
9．（2022·湖北·车城高中高一阶段练习）设全集，集合，则的子集为（       ）
A． B． C． D．
【答案】AD
【解析】
【分析】
根据补集和子集的定义即可求出答案.
【详解】
因为，集合的子集有：，.
故选：AD.
10．（2022·全国·高一课时练习）已知全集，集合，，则使成立的实数的取值范围可以是（　　）
A． B．
C． D．
【答案】ABC
【解析】
【分析】
讨论和时，计算，根据列不等式，解不等式求得的取值范围，再结合选项即可得正确选项.
【详解】
当时，，即，此时，符合题意，
当时，，即，
由可得或，
因为，所以或，可得或，
因为，所以，
所以实数的取值范围为或，
所以选项ABC正确，选项D不正确；
故选：ABC.
11．（2022·江西·高一期中）已知集合M､N的关系如图所示，则下列结论中正确的是（       ）


A． B．
C． D．
【答案】BD
【解析】
【分析】
根据Venn图和交并补的定义逐一判断即可.
【详解】
由题意得，对于A，C，设，，
则，，则，故A错误；，故C错误；
对于B，由Venn图和知，，故B正确；
对于D，因为，所以，故D正确.
故选:BD.
12．（2022·山东泰安·高一期中）已知为全集，则下列说法正确的是（       ）
A．若，则 B．若，则或
C．若，则 D．若，则
【答案】ACD
【解析】
【分析】
利用集合的交、并、补运算即可求解.
【详解】
A，因为，，
所以，说法正确；
B，若，则集合不一定为空集，
只需两个集合中无公共元素即可，B说法错误，；
C，因为，，
所以，说法正确；
D，，即集合中均无任何元素，可得，D说法正确.
故选：ACD
三、填空题
13．（2022·北京四中高一阶段练习）某班有学生55人，其中音乐爱好者34人，体育爱好者43人，还有4人既不爱好体育也不爱好音乐，则班级中即爱好体育又爱好音乐的有___________人．
【答案】26
【解析】
【分析】
运用集合间关系即可得出结果.

【详解】
由题意作出Venn图，从而求解人数．
解：作Venn图如图，
，
，
；
故．
故答案为：26．

14．（2022·全国·高一专题练习）设集合，，，则集合的子集个数为______．
【答案】4
【解析】
【分析】
解一元二次不等式，再结合得集合，从而可求得集合，，再用列举法列出集合的子集即可.
【详解】
解不等式得，，
所以，
所以，，
集合的子集个数为4，列举如下：，，，.
故答案为：4.
15．（2022·安徽省太和中学高一阶段练习）设集合，，若，则实数的取值范围是_______.
【答案】或
【解析】
先求得集合A，由已知得，分和两种情况建立不等式，可求得答案．
【详解】
集合或，，∵，∴，
当，即时，，符合题意；
当，即时，或，得.综上，或.
故答案为：或．
【点睛】
本题考查集合间的运算和集合间的包含关系.在解决有关A⊆B集合问题时，往往忽略空集的情况，一定先考虑是否成立，以防漏解.
16．（2022·湖南师大附中高一阶段练习）已知，，且，则的值等于_____．
【答案】
【解析】
根据，可得，即可解得p的值，进而可求得集合，又根据，可得，即，即可解得q的值，即可得答案.
【详解】
因为，
所以，则，解得，
所以，解得，
又因为，
所以，即，
所以，解得，
所以，
故答案为：
【点睛】
本题考查元素与集合的关系，重点考查分析理解，逻辑推理能力，属基础题.
四、解答题
17．（2022·浙江金华第一中学高一阶段练习）已知全集为，集合，．
(1)求，；
(2)若，且，求实数的取值范围．
【答案】(1)；
(2)
【解析】
【分析】
（1）化简集合，根据集合的并集、补集、交集运算可得结果；
（2）分类讨论集合，根据子集关系列式可求出结果.
(1)
，
，
或，
.
(2)
因为，所以，
当，即时，，符合题意；
当，即时，，解得，
综上所述：实数的取值范围是.
18．（2022·福建省德化第一中学高一阶段练习）设全集，集合
(1)求；
(2)若集合，且，求a的取值范围．
【答案】(1)，
(2)
【解析】
【分析】
（1）根据交集，并集和补集的定义即可得出答案；
（2）根据，可得，从而可得出答案.
(1)
解：，
或，
，

(2)
解：，
，，
所以，解得.
19．（2022·湖北·襄阳市第二十四中学高一阶段练习）已知且，或.求：
(1)，；
(2).
【答案】(1)或;

(2)

【解析】
【分析】
（1）先求解集合A，再根据交集和并集的概念写出结论即可；
（2）先分别求解集合A和集合B的补集，再根据交集的概念写出答案.
(1)
根据可知，
又或
或;
.

(2)
根据题意，或;
所以.
20．（2022·北京·高一期末）已知集合，．
(1)求集合；
(2)当时，求；
(3)若，求的取值范围．
【答案】(1)或
(2)
(3)
【解析】
【分析】
（1）根据题干条件以及补集的定义可得解；
（2）根据题干条件以及交集的定义可得解；
（3）根据（1）可得或，结合，分析即得解
(1)
由题意，
故或
(2)
当时，
故
(3)
由（1）或

若，则
解得
21．（2022·安徽宣城·高一期中）已知表示实数集，集合，集合．
(1)当时，求；
(2)若，求实数m的取值范围；
(3)若，求实数m的取值范围．
【答案】(1)
(2)
(3)
【解析】
【分析】
（1）解不等式求出集合A，再求出集合A的补集，然后求出，
（2）由，可得，从而得，解不等式组可得答案，
（3）由，分和两种情况求解即可
(1)
因为，所以或，
当时，，
所以
(2)
由知，所以，得，
即实数m的取值范围为
(3)
由，得
①当，即时，，符合题意；
②当，即时，若要满足题意，
则需或，得．
综上，可知实数m的取值范围为．
22．（2022·河北·石家庄市第四十一中学高一阶段练习）设集合，，．
（1）若，求a的取值范围；
（2）若，求a的取值范围．
【答案】（1）或
（2）
【解析】
【分析】
（1）先确定集合或，计算方程的判别式，然后分类讨论，当时，确定集合，此时不成立，舍去；当时，确定集合，利用补集的思想，求时取值范围，再求补集，即可.
（2）根据，得到，再根据原命题与其逆否命题等价，则，即，解不等式组，即可.
【详解】
（1）或，即或

当，即时，，此时不成立，舍去
当，即时，方程的两根为，
若使得成立，则需或，
即或，解得.
则成立时，或
综上所述：或.
（2）即
由（1）可知或，则，
当，即时，成立
当，即时，，若使得成立，
则需满足，即，解得（舍去）
综上所述.
【点睛】
本题考查利用集合之间的关系求参数的取值范围，注意分类讨论以及补集思想的运用，属于难度较大的一道题.