2021-2022学年山东省临沂市罗庄区八年级（下）期末数学试卷（Word解析版）

这是一份2021-2022学年山东省临沂市罗庄区八年级（下）期末数学试卷（Word解析版），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题（本大题共12小题，共36分）
下列算式正确的是( )
A. 5+5=10B. (-4)×(-9)=-4×-9
C. 22÷2=2D. 43-3=3
已知一个直角三角形的两边长分别为3和4，那么第三边的平方是( )
A. 25B. 5C. 5或7D. 7或25
一次函数y=-2x-3的图象不经过( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
如图，两个等宽的矩形纸条交叉叠放在一起，若重合部分构成的四边形为ABCD，求证：四边形ABCD是菱形．
下列说法正确的是( )
A. 证法1还需要证明三角形全等，该证明才完整
B. 证法1的证明过程是严谨完整的
C. 证法2用特殊到一般法证明了该问题
D. 证法2只要测量够一百个四边形的边长进行验证，就能证明该问题
在对一组样本数据进行分析时，小凡列出了方差的计算公式：S2=15[(8-x-)2+2(6-x-)2+(9+x-)2+(11-x-)2]，下面结论错误的是( )
A. 众数是6B. 方差是3.6C. 平均数是8D. 中位数是6
若菱形的周长为8，高为1，则菱形两邻角的度数之比是( )
A. 3:1B. 4:1C. 5:1D. 6:1
如图1，Rt△ABC中，点P从点C出发，匀速沿CB-BA向点A运动，连接AP，设点P的运动距离为x，AP的长为y，y关于x的函数图象如图2所示，则当点P为BC中点时，AP的长为( )
A. 5B. 8C. 52D. 213
如图，▱ABCD中，AB=6，AD=10，按以下步骤作图：
①以点B为圆心，适当长为半径画弧，分别交BA于点E，交BC于点F；
②分别以点E，F为圆心，大于12EF的长为半径画弧，两弧在∠ABC内相交于点P；
③画射线BP，交AD于点Q，交对角线AC于点O．
若BA⊥CA，则AO的长度为( )
A. 3B. 3C. 32D. 22
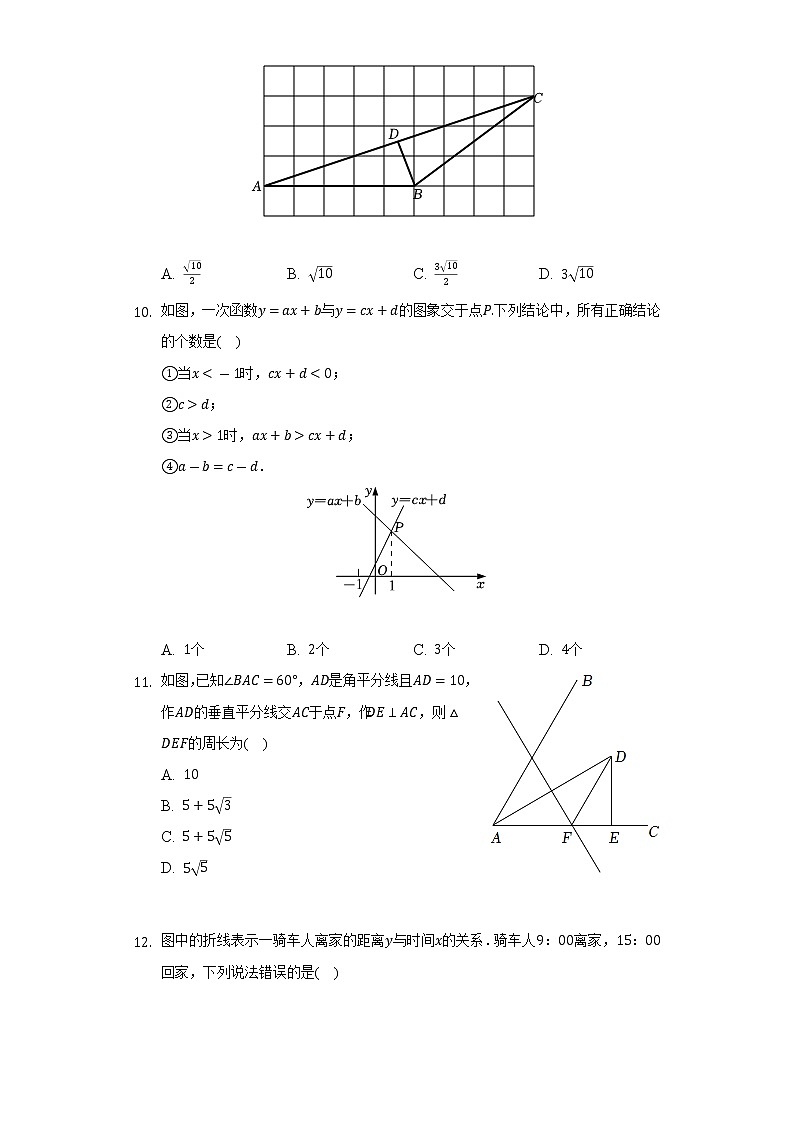
如图，在9×5的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，若BD是∠ABC的平分线，则BD的长为( )
A. 102B. 10C. 3102D. 310
如图，一次函数y=ax+b与y=cx+d的图象交于点P.下列结论中，所有正确结论的个数是( )
①当x<-1时，cx+d<0；
②c>d；
③当x>1时，ax+b>cx+d；
④a-b=c-d．
A. 1个B. 2个C. 3个D. 4个
如图，已知∠BAC=60°，AD是角平分线且AD=10，作AD的垂直平分线交AC于点F，作DE⊥AC，则△DEF的周长为( )
A. 10
B. 5+53
C. 5+55
D. 55
图中的折线表示一骑车人离家的距离y与时间x的关系．骑车人9：00离家，15：00回家，下列说法错误的是( )
A. 他离家最远是45km
B. 他开始第一次休息离家30km
C. 他在10：30～12：30的平均速度是7.5km/h
D. 他返家时的平均速度是25km/h
二、填空题（本大题共1小题，共16分）
(1)若要使3+x有意义，则x的取值范围为______．
(2)如图，点P是矩形ABCD的对角线AC上的一点，过点P作EF//BC，分别交AB、CD于E，F，连接PB，PD.若AE=2，PF=6，则图中阴影部分的面积是______．
(3)若x+1x=6(0(4)如图，在平面直角坐标系中，点A1，A2，A3…都在x轴上，点B1，B2，B3…都在直线y=x上，△OA1B1，△B1A1A2，△B2B1A2，△B2A2A3，△B3B2A3…都是等腰直角三角形，且OA1=1，则点B4的坐标是，点Bn的坐标是______．
三、解答题（本大题共7小题，共68分）
计算：(3+2-3)(3-2+3)．
某社区为了加强社区居民对冬奥会的了解，通过网络宣传冬奥会知识，并鼓励社区居民在线参与作答《2022年北京冬奥会知识点》模拟试卷．社区管理员随机从甲、乙两个小区各抽取10名人员的答卷成绩，并对他们的成绩(单位：分)进行统计、分析，过程如下：收集数据：
甲小区85 80 95 100 90 95 85 65 75 85；
乙小区80 60 80 95 65 100 90 85 85 80；
整理数据：
分析数据：
应用数据：
(1)填空：a=______，b=______，c=______，d=______；
(2)你认为甲、乙两个小区哪一个对冬奥会知识掌握更好？请写出理由．(一条即可)
(3)若甲小区共有300人参与答卷，乙小区共有400人参与答卷，请估计两个小区成绩大于80分的总人数．
如图，在△ABC中，内角A、B、C所对的边分别为a、b、c．
(1)若a=6，b=8，c=12，请直接写出∠A与∠B的和与∠C的大小关系；
(2)求证：△ABC的内角和等于180°；
(3)若aa-b+c=12(a+b+c)c，求证：△ABC是直角三角形．
如图，在▱ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．
(1)证明：四边形EHFG是平行四边形；
(2)当▱ABCD具备怎样的条件时，四边形EHFG是菱形？请直接写出条件，无需说明理由．
在平面直角坐标系中，y关于x的一次函数y=x+4-c(c为常数)，其图象与y轴交于点A，与x轴交于点B．
(1)当c=2时，OA=______；
(2)若△OAB的面积为8．
①求出满足条件的一次函数表达式；
②若点A在y轴正半轴，点B在x轴负半轴上，且点C在线段AB上，当S△OAC=7S△OBC时，请直接写出点C的坐标．
小慧根据学习函数的经验，对函数y=|x-1|的图象与性质进行了探究．
下面是小慧的探究过程，请补充完成：
(1)画出函数图象：
列表，找出y与x的几组对应值．
描点，连线得到函数图象：
(2)通过观察图象，写出该函数的两条性质：(从y随x变化、对称性、最大值或最小值等方面描述)
①；②；
(3)设(x1,y1)，(x2,y2)是函数图象上的点，若x1+x2=2，证明：y1=y2．
已知正方形ABCD，E，F为平面内两点．
【探究建模】：
(1)如图1，当点E在边AB上时，DE⊥DF，且B，C，F三点共线．求证：AE=CF；
【类比应用】：
(2)如图2，当点E在正方形ABCD外部时，DE⊥DF，AE⊥EF，且E，C，F三点共线．若AE=5，CE=25，求点D到直线EF的距离；
【拓展迁移】：
(3)如图3，当点E在正方形ABCD外部时，AE⊥EC，AE⊥AF，DE⊥BE，且D，F，E三点共线，DE与AB交于G点．若DF=2，AE=2，求正方形ABCD对角线的长．
答案和解析
1.【答案】C
【解析】解；A.原式=25，所以A选项不符合题意；
B.原式=4×9=4×9，所以B选项不符合题意；
C.原式=2，所以C选项符合题意；
D.原式=33，所以D选项不符合题意；
故选：C．
利用二次根式的加减法对A、D进行判断；根据二次根式的乘法法则对B进行判断；根据二次根式的除法法则对C进行判断．
本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法法则和除法法则是解决问题的关键．
2.【答案】D
【解析】解：当边长为4的边为直角边时，第三边的平方为32+42=25；
当边长为4的边为斜边时，第三边的的平方为42-32=7；
故D选项正确．
故选：D．
由题意4这条边可以为直角边，也可以是斜边，从而分两种情况进行讨论解答．
本题主要考查了勾股定理的运用，能够利用分类讨论思想解答是解决问题的关键．
3.【答案】A
【解析】解：∵y=-2x-3
∴k<0，b<0
∴y=-2x-3的图象经过第二、三、四象限，不经过第一象限
故选：A．
因为k=-2<0，一次函数图象过二、四象限，b=-3<0，图象过第三象限．
一次函数图象的四种情况：
①当k>0，b>0，函数y=kx+b的图象经过第一、二、三象限，y的值随x的值增大而增大；
②当k>0，b<0，函数y=kx+b的图象经过第一、三、四象限，y的值随x的值增大而增大；
③当k<0，b>0时，函数y=kx+b的图象经过第一、二、四象限，y的值随x的值增大而减小；
④当k<0，b<0时，函数y=kx+b的图象经过第二、三、四象限，y的值随x的值增大而减小．
4.【答案】B
【解析】解：证法1证明过程是严谨完整的，证法2是用特殊值法，这方法不能用于这题证明，
故选：B．
利用矩形的性质和菱形的判定依次判断两个证明方法可求解．
本题考查了矩形的性质，菱形的判定，面积法等知识，掌握矩形的性质是解题的关键．
5.【答案】D
【解析】解：由方差的计算公式得出这组数据为6、6、8、9、11，
所以这组数据的众数为6，平均数为6+6+8+9+115=8，中位数为8，
方差为15×[2×(6-8)2+(8-8)2+(9-8)2+(11-8)2]=3.6，
故选：D．
根据方差、众数、中位数及平均数的定义求解即可．
本题主要考查方差，解题的关键是掌握中位数、众数、平均数和方差的定义．
6.【答案】C
【解析】
【分析】
本题考查了菱形的性质、含30°角的直角三角形的判定；熟练掌握菱形的性质和含30°角的直角三角形的判定是解决问题的关键．先根据菱形的性质求出边长AB=2，再根据直角三角形的性质求出∠B=30°，得出∠DAB=150°，即可得出结论．
【解答】
解：如图所示：∵四边形ABCD是菱形，菱形的周长为8，
∴AB=BC=CD=DA=2，∠DAB+∠B=180°，
∵AE=1，AE⊥BC，
∴AE=12AB，
∴∠B=30°，
∴∠DAB=150°，
∴∠DAB：∠B=5：1；
故选C．
7.【答案】D
【解析】
【分析】
本题考查了动点问题的函数图象：通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．
通过观察图2可以得出AC=6，BC=a，AB=a+2，由勾股定理可以求出a的值，从而得出BC=8，AB=10，当P为BC的中点时CP=4，由勾股定理求出AP长度．
【解答】
解：因为P点是从C点出发的，C为初始点，
观察图象x=0时y=6，则AC=6，P从C向B移动的过程中，AP是不断增加的，
而P从B向A移动的过程中，AP是不断减少的，
因此转折点为B点，P运动到B点时，即x=a时，BC=PC=a，此时y=a+2，
即AP=AB=a+2，AC=6，BC=a，AB=a+2，
∵∠C=90°，
由勾股定理得：(a+2)2=62+a2，
解得：a=8，
∴AB=10，BC=8，
当点P为BC中点时，CP=4，
∴AP=AC2+CP2=62+42=213，
故选D．
8.【答案】A
【解析】解：∵四边形ABCD为平行四边形，
∴BC=AD=10，
∵BA⊥CA，
∴∠BAC=90°，
在Rt△ABC中，AC=BC2-AB2=102-62=8，
由作法得BQ平分∠ABC，
∴点O到BA的距离等于点O到BC的距离，
∴S△ABO：S△BCO=AB：BC=6：10=3：5，
∵S△ABO：S△BCO=OA：OC，
∴OA：OC=3：5，
∴OA：AC=3：8，
∴OA=38AC=38×8=3．
故选：A．
先根据平行四边形的性质得到BC=AD=10，再利用勾股定理计算出AC=8，利用基本作图得到BQ平分∠ABC，则根据角平分线的性质得到点O到BA的距离等于点O到BC的距离，接着利用三角形的面积公式得到S△ABO：S△BCO=AB：BC=OA：OC，所以OA=38AC．
本题考查了作图-复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了角平分线的性质和平行四边形的性质．
9.【答案】A
【解析】解：由题意可得，BC=32+42=5，AB=5，AC=32+92=310，
∴AB=BC，
∵BD是∠ABC的平分线，
∴BD⊥AC，AD=CD=12AC=3210，
∴BD=AB2-AD2=52-(3210)2=102，
故选：A．
由勾股定理求出BC=5，AC=310，AB=5，得出AB=BC，由等腰三角形的性质得出BD⊥AC，AD=CD，根据勾股定理可求出答案．
本题考查了勾股定理，等腰三角形的性质，熟练掌握勾股定理是解题的关键．
10.【答案】B
【解析】解：由图象可知一次函数y=cx+d的图象经过一、二、三象限，当x=-1时，y<0，
∴当x<-1时，cx+d<0，
∴-c+d<0，
∴c>d，
故①②选项符合题意；
由图象可知，当x<1时，ax+b>cx+d，
故③选项不符合题意；
∵一次函数y=ax+b与y=cx+d的图象交于点P，且P的横坐标为1，
∴a+b=c+d，
故④选项不符合题意；
故选：B．
根据一次函数的图象和性质进行判断即可．
本题考查了一次函数的图象和性质，熟练掌握一次函数图象与系数的关系是解题的关键．
11.【答案】B
【解析】解：∵AD的垂直平分线交AC于点F，
∴DF=AF，
∵∠BAC=60°，AD是角平分线，
∴∠DAC=30°，
∵DE⊥AC，AD=10，
∴DE=12AD=5，
根据勾股定理，得AE=AD2-DE2=53，
∴△DEF的周长=AE+DE=5+53，
故选：B．
根据线段垂直平分线的性质可得DF=AF，根据含30°角的直角三角形的性质可得DE=5，再根据勾股定理可得AE的长，进一步即可求出△DEF的周长．
本题考查了线段垂直平分线的性质，直角三角形的性质，角平分线的定义，勾股定理等，熟练掌握这些知识是解题的关键．
12.【答案】D
【解析】解：由图象可知，他离家最远是45km，故A正确，不符合题意；
他开始第一次休息离家30km，故B正确，不符合题意；
他在10：30～12：30的平均速度是(45-30)÷2=7.5(km/h)，故C正确，不符合题意；
他返家时的平均速度是45÷(15-13.5)=30(km/h)，故D错误，符合题意；
故选：D．
由函数图象直接可判断A和B，根据平均速度=路程时间可判断C和D．
本题考查一次函数的应用，解题的关键是从函数图象中获取有用信息，然后再根据信息进行分析、解释即可．
13.【答案】x≥-3 12 -2 (2n-1,2n-1)
【解析】解：(1)在实数范围内，使3+x有意义，
则3+x≥0，
解得：x≥-3．
故答案为：x≥-3．
(2)作PM⊥AD于M，交BC于N．

则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，
∴S△ADC=S△ABC，S△AMP=S△AEP，S△PBE=S△PBN，S△PFD=S△PDM，S△PFC=S△PCN，
∵MP=AE=2，
∴S△DFP=S△PBE=12×2×6=6，
∴S阴=6+6=12，
故答案为：12．
(3)∵x+1x=6，
∴(x+1x)2=6，
∴(x-1x)2+4=6，
∴|x-1x|=2，
∵0∴x-1x=-2．
故答案为：-2；
(4)∵OA1=1，
∴点A1的坐标为(1,0)，
∵△OA1B1是等腰直角三角形，
∴A1B1=1，
∴B1(1,1)，
∵△B1A1A2是等腰直角三角形，
∴A1A2=1，B1A2=A1B12+A1A22=12+12=2，
∵△B2B1A2为等腰直角三角形，
∴A2A3=2，
∴B2(2,2)，
同理可得，B3(22,22)，B4(23,23)，…，Bn(2n-1,2n-1).
故答案为：(2n-1,2n-1).
(1)直接利用二次根式的定义分析得出答案；
(2)由矩形的性质可证明S△PEB=S△PFD，即可求解．
(3)把已知条件两边平方得到(x+1x)2=6，再根据完全平方公式得到(x-1x)2+4=6，则利用二次根式的性质得结论．
(4)由OA1=1得到点B1的坐标，然后利用等腰直角三角形的性质得到点A2的坐标，进而得到点B2的坐标，然后再一次类推得到点Bn的坐标．
本题考查了二次根式有意义的条件，矩形的性质、三角形的面积，二次根式的化简求值，一次函数图象上点的坐标特征、等腰直角三角形的性质，解题的关键是通过等腰直角三角形的性质依次求出系列点B的坐标找出规律．
14.【答案】解：(3+2-3)(3-2+3)
=[3+(2-3)][3-(2-3)]
=3-(2-3)2
=3-2+62-9
=-8+62．
【解析】先将式子变形，然后根据平方差公式和完全平方公式计算即可．
本题考查二次根式的混合运算，熟练掌握运算法则是解答本题的关键．
15.【答案】1 3 82.5 85
【解析】解：(1)由甲小区抽取的10名人员的答卷成绩可知a=1，
由乙小区抽取的10名人员的答卷成绩可知b=3，
把乙小区抽取的10名人员的答卷成绩排序为：60，65，80，80，80，85，85，90，95，100，
则乙小区成绩的中位数c=80+852=82.5(分)，
由甲小区抽取的10名人员的答卷成绩中85出现次数最多，故众数d=85．
故答案为：1，3，90，82.5；85
(2)甲小区对冬奥会知识掌握更好，
理由：甲小区的平均数、中位数、众数均大于乙小区的；
(3)估计甲小区成绩大于80分的人数为：300×3+410+400×2+310=450(人)，
答：估计两个小区成绩大于80分的总人数为450人．
(1)直接根据题意、平均数、中位数的定义求解即可；
(2)直接比较两小区的平均数、中位数、众数即可；
(3)利用样本估计总体即可．
本题主要考查统计图表及数据的收集宇整理知识，熟练掌握众数、平均数、中位数的定义、用样本估计总体的方法是解题的关键．
16.【答案】解：(1)∵在△ABC中，a=6，b=8，c=12，
∴∠A+∠B<∠C；
(2)如图，过点A作MN//BC，
∵MN//BC，
∴∠MAB=∠B，∠NAC=∠C(两直线平行，同位角相等)，
∵∠MAB+∠BAC+∠NAC=180°(平角的定义)，
∴∠B+∠BAC+∠C=180°(等量代换)，
即：三角形三个内角的和等于180°；
(3)∵aa-b+c=12(a+b+c)c，
∴ac=12(a+b+c)(a-b+c)=12[(a2+2ac+c2)-b2]，
∴2ac=a2+2ac+c2-b2，
∴a2+c2=b2，
∴△ABC是直角三角形．
【解析】(1)根据三角形中大角对大边，即可得到结论；
(2)画出图形，写出已知，求证；过点A作直线MN//BC，根据平行线性质得出∠MAB=∠B，∠NAC=∠C，代入∠MAB+∠BAC+∠NAC=180°即可求出答案；
(3)化简等式即可得到a2+c2=b2，根据勾股定理的逆定理即可得到结论．
本题考查了三角形内角和定理以及平行线的性质等知识，根据证明过程运用转化思想是解题的关键．
17.【答案】(1)证明：∵四边形ABCD是平行四边形，
∴AB//CD，AB=CD，
∵E、F分别是AB、CD的中点，
∴AE=12AB，CF=12CD，
∴AE=CF，
∴四边形AECF是平行四边形，
∴AF//CE．
同理：DE//BF，
∴四边形EHFG是平行四边形；
(2)解：当▱ABCD是矩形时，四边形EHFG是菱形．理由如下：
∵四边形ABCD是矩形，
∴∠ABC=∠DCB=90°，
∵E、F分别是AB、CD的中点，
∴EE=12AB，CF=12CD，
∴BE=CF，
在△EBC与△FCB中，
BE=CF∠ABC=∠DCBBC=CB，
∴△EBC≌△FCB(SAS)，
∴CE=BF，∠ECB=∠FBC，
∴BH=CH，
∴CE-CH=BF=BH，
即EH=FH，
∴平行四边形EHFG是菱形．
【解析】(1)先证四边形AECF是平行四边形，得AF//CE.同理：DE//BF，再由平行四边形的判定即可得出结论；
(2)证△EBC≌△FCB(SAS)，得CE=BF，∠ECB=∠FBC，得BH=CH，再证EH=FH，即可得出结论．
本题考查了平行四边形的判定与性质，菱形的判定，矩形的性质，全等三角形的判定与性质，等腰三角形的判定等知识，熟练掌握菱形的判定和平行四边形的判定与性质是解题的关键．
18.【答案】2
【解析】解：(1)当c=2时，y=x+2，
当x=0时，y=2，
∴A(0,2)，
∴OA=2；
故答案为：2；
(2)①对于y=x+4-c(c为常数)，
当x=0时，y=4-c，
当y=0时，x=c-4，
∴A(0,4-c)，B(c-4,0)，
∴OA=|4-c|，OB=|c-4|，
∵△OAB的面积为8，
∴12×|4-c|×|c-4|=8，
∴(c-4)2=16，
解得：c=8或0，
∴一次函数表达式为：y=x-4或y=x+4；
②当点C在线段AB的延长线上时，
∵点A在y轴正半轴，点B在x轴负半轴上，
∴y=x+4，
∴A(0,4)，B(-4,0)，
∴OA=OB=4，
∴AB=OA2+OB2=42，∠ABO=45°，
设点O到直线AB的距离为h，
∵S△OAC=7S△OBC，
∴12×AC×h=12×BC×h，
∴AC=7BC，
∴AB=6BC，
∴BC=16×42=223，
过点C作CD⊥x轴于点D，
∵∠DBC=∠ABO=45°，
BC2+BD2=BC2，
∴BD=CD=23，
∴C(-143,-23)；
当点C在线段AB上时，
∵AC=7BC，AC+BC=AB=42，
∴8BC=42，
∴BC=22，
∴C(-72,12)；
综上所述，点C的坐标为(-143,-23)或(-72,12).
(1)求出点A坐标即可得出答案；
(2)①根据三角形面积为8列方程求出c的值即可得到一次函数的解析式；
②当点C在线段AB的延长线上时，求出此时A，B点的坐标，求出AB的长，根据S△OAC=7S△OBC，得到AC=7BC，进而AB=6BC，求出BC的长，过点C作CD⊥x轴于点D，根据勾股定理得到BD=CD=23，即可得到点C的坐标；当点C在线段AB上时，根据AC=7BC，AC+BC=AB=42，求出BC的长即可得到点C的坐标．
本题考查了一次函数的性质，体现了分类讨论的思想，一次函数图象上点的坐标特征，根据S△OAC=7S△OBC，得到AC=7BC是解题的关键．
19.【答案】-2 -1 0 1 2 3 4 3 2 1 0 1 2 3
【解析】解：(1)列表：
描点，连线得到函数图象如图：

(2)由函数图象可知，①函数图象关于直线x=1对称；
②函数的最小值为0．
(3)由图象可知，函数图象关于直线x=1对称，
∵(x1,y1)，(x2,y2)是函数图象上的点，且x1+x2=2，
∴(x1,y1)，(x2,y2)关于直线x=1对称，
∴y1=y2．
(1)列表、在坐标系内描出各点，再顺次连接即可；
(2)观察图象即可得到；
(3)根据题意(x1,y1)，(x2,y2)关于直线x=1对称，根据函数的性质即可得到结论．
本题考查的是一次函数的性质，根据题意画出函数图象，利用数形结合求解是解答此题的关键．
20.【答案】(1)证明：∵四边形ABCD是正方形，
∴DA=DC，∠A=∠ADC=∠DCB=∠DCF=90°，
∵DE⊥DF，
∴∠EDF=∠ADC=90°，
∴∠ADE=∠CDF，
在△DAE和△DCF中，
∠ADE=∠CDFDA=DC∠A=∠DCF，
∴△DAE≌△DCF(ASA)，
∴AE=CF．
(2)解：猜想：EA+EC=2DE．
理由：如图2，
∵四边形ABCD是正方形，
∴DA=DC，∠ADC=90°，
∵DE⊥DF，AE⊥EF，
∴∠AEF=∠EDF=90°，
∴∠ADC=∠EDF，
∴∠ADE=∠CDF，
∵∠ADC+∠AEC=180°，
∴∠DAE+∠DCE=180°，
∵∠DCF+∠DCE=180°，
∴∠DAE=∠DCF，
∴△DAE≌△DCF(AAS)，
∴AE=CF=5，
∵CE=25，∴EF=CE+CF=35，
过点D作DH⊥EF于H，
∵DE=DF，
∴DH=12EF=352，
即点D到直线EF的距离为352；
(3)解：如图3中，连接AC，取AC的中点O，连接OE，OD．

∵四边形ABCD是正方形，AE⊥EC，
∴∠AEC=∠ADC=90°，
∵OA=OC，
∴OD=OA=OC=OE，
∴A，E，C，D四点共圆，
∴∠AED=∠ACD=45°，
∴∠AED=∠DEC=45°，
由(2)可知，AE+EC=2DE，
∵AE⊥AF，
∴∠EAF=90°，
∴∠AEF=∠AFE=45°，
∴AE=AF=2，
∴EF=2AE=2，
过点A作AM⊥DE于M，
∴AM=FM=12EF=1，
∴DM=DF+FM=3，
根据勾股定理得，AD2=DM2+AM2=10，
∴AD=10，
∴AC=2AD=25，
即正方形ABCD的对角线的长为25．
【解析】(1)证明△DAE≌△DCF(ASA)，可得结论．
(2)猜想：EA+EC=2DE.如图2中，证明△DAE≌△DCF，推出DE=DF，AE=CF，最后用三角形的面积求解，即可求出答案．
(3)如图3中，连接AC，取AC的中点O，连接OE，OD.证明∠AED=∠DEC=45°，最后构造直角三角形，即可求出答案．
本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，四点共圆，圆周角定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用建模的思想思考问题，属于中考压轴题．
题号
一
二
三
总分
得分
证法一：设两张等宽的纸条为h
∵纸条的对边平行，
∴AD//BC，AB//DC
∴四边形ABCD是平形四边，
∵S四边形ABCD=BC⋅h=AB⋅h
∴BC=AB，四边形ABCD是菱形．
证法二：
∵AB=0.9cm，BC=0.9cm，CD=09cm，AD=0.9cm，(直尺测量)；
∴AB=BC=CD=AD；
∴四边形ABCD是菱形．
成绩x(分)
60≤x≤70
708090甲小区
a
2
4
3
乙小区
2
3
b
2
统计量
平均数
中位数
众数
甲小区
85.5
85
d
乙小区
82
c
80
x
…
______
______
______
______
______
______
______
…
y
…
______
______
______
______
______
______
______
…
x
…
-2
-1
0
1
2
3
4
…
y
…
3
2
1
0
1
2
3
…