2022届西藏自治区拉萨中学高三第七次月考数学（文）试题含解析

2022届西藏自治区拉萨中学高三第七次月考数学（文）试题

一、单选题

1．复数的虚部是（       ）

A． B． C． D．

【答案】B

【分析】先根据复数的四则运算法则求出，再根据复数的虚部的定义即可求出．

【详解】因为，所以的虚部是．

故选：B．

2．设集合、均为的子集，如图，表示区域（       ）

A．Ⅰ B．II

C．III D．IV

【答案】B

【分析】根据交集与补集的定义可得结果.

【详解】由题意可知，表示区域II.

故选：B.

3．在中，若，则B为(       )

A． B．或 C．或 D．

【答案】B

【分析】根据正弦定理即可求出B.

【详解】，

由正弦定理可知，

，

，

或．

故选：B．

4．“”是方程表示的曲线为椭圆的（       ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】B

【分析】根据椭圆的几何性质， ， ，但 ，

容易判断充要条件.

【详解】当 时，m-2=3-m，此时 ，表示的是圆心在原点，

半径为 的圆，

但如果 表示的是椭圆，则必定有 ，

根据充分必要条件的定义，“”是表示椭圆的必要不充分条件；

故选：B.

5．以下给出的是计算＋＋＋…＋的值的一个程序框图，其中判断框内应填入的条件是

A．i<20 B．i>10 C．i<10 D．i≤10

【答案】D

【详解】试题分析：由程序框图，知时要执行循环体计算，而时要退出循环体，输出，

此时，故选D．

【解析】程序框图

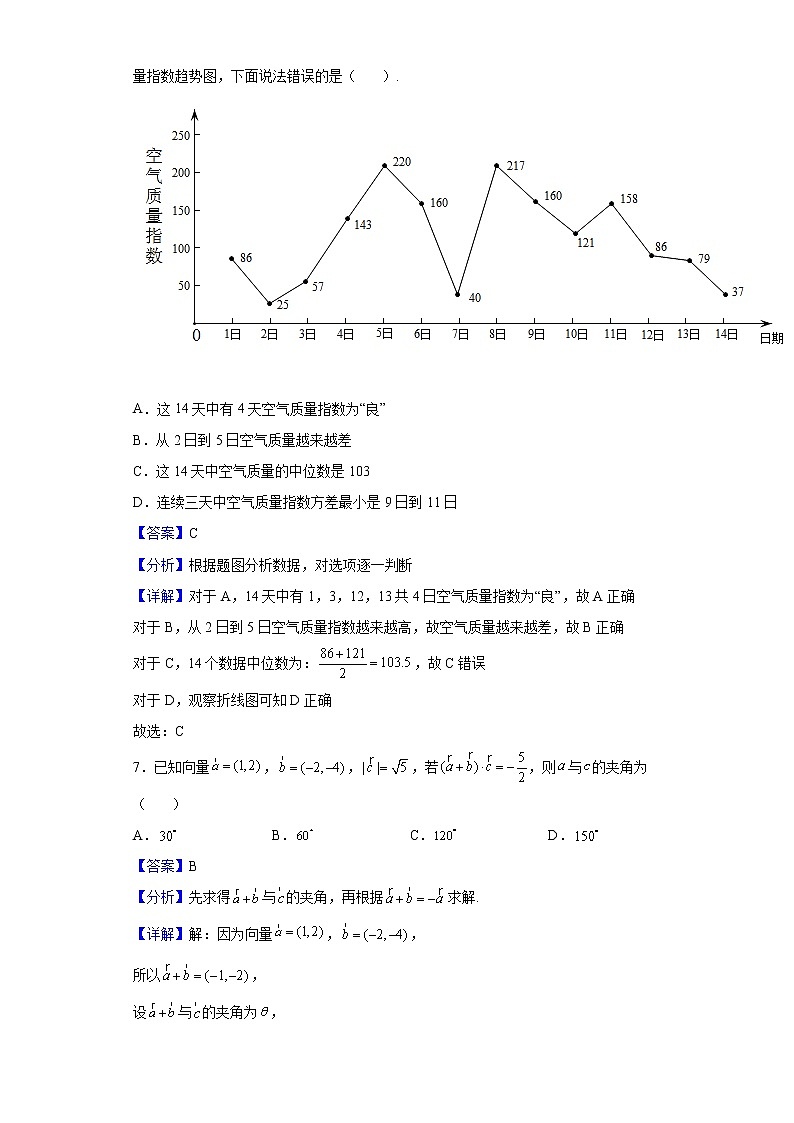
6．空气质量指数大小分为五级指数越大说明污染的情况越严重，对人体危害越大，指数范围在：，，，，分别对应“优”、“良”、“轻中度污染”、“中度重污染”、“重污染”五个等级，如图是某市连续14天的空气质量指数趋势图，下面说法错误的是（       ）.

A．这14天中有4天空气质量指数为“良”

B．从2日到5日空气质量越来越差

C．这14天中空气质量的中位数是103

D．连续三天中空气质量指数方差最小是9日到11日

【答案】C

【分析】根据题图分析数据，对选项逐一判断

【详解】对于A，14天中有1，3，12，13共4日空气质量指数为“良”，故A正确

对于B，从2日到5日空气质量指数越来越高，故空气质量越来越差，故B正确

对于C，14个数据中位数为：，故C错误

对于D，观察折线图可知D正确

故选：C

7．已知向量，，，若，则与的夹角为（       ）

A． B． C． D．

【答案】B

【分析】先求得与的夹角，再根据求解.

【详解】解：因为向量，，

所以，

设与的夹角为，

因为，，

所以，

则，

因为，

所以，

因为，

所以与的夹角为，

故选：B

8．若直线始终平分圆的周长，则的最小值为（       ）

A．1 B．2 C．3 D．4

【答案】D

【分析】根据给定条件，求出圆心坐标，再借助“1”的妙用计算作答.

【详解】圆，即的圆心为，依题意，点在直线上，

则有，整理得，而，

于是得，当且仅当时取“=”，

所以的最小值为4.

故选：D

9．已知一个几何体的三视图如图所示，俯视图为等腰三角形，则该几何体的体积为（       ）

A． B． C．2 D．

【答案】B

【分析】根据三视图可得如图所示的几何体，根据椎体的体积公式以及三视图中的数据可求该几何体的体积.

【详解】

复原后的几何体为如图所示的三棱锥，其底面为等腰三角形，

该三角形的底边长为2，高为2，棱锥的高为2，

故体积为.

故选：B．

10．有如下命题：①若幂函数的图象过点，则；

②函数的图象恒过定点；

③函数有两个零点；

④若函数在区间上的最大值为4，最小值为3，则实数m的取值范围是．

其中真命题的序号为（       ）．

A．①② B．②④ C．①④ D．②③

【答案】B

【分析】①求出幂函数的解析式，利用其单调性判断；②令求解判断；③在同一坐标系中作出的图象判断； ④作出函数的图象判断.

【详解】①设幂函数为，因为的图象过点，所以，解得，则，在上递减，在上递减，所以，故错误；

②令，解得，此时，所以函数的图象恒过定点，故正确；

③令，得，在同一坐标系中作出的图象，如图所示，

由图象知：有1个交点，即函数有1个零点，故错误；

④函数的图象，如图所示：

，

由图象知：若在区间上的最大值为4，最小值为3，则实数m的取值范围是，故正确．

故选：B

11．已知在处的切线倾斜角为，则的值为（       ）

A．7 B． C．5 D．-3

【答案】B

【分析】由导数的几何意义求出切线斜率得出，再由二倍角的正余弦公式及同角三角函数的基本关系化简求值即可.

【详解】因为，

所以，

所以

.

故选：B

12．已知函数是奇函数．若将曲线向左平移个单位长度后，再向上平移个单位长度得到曲线，若关于x的方程在有两个不相等实根，则实数m的取值范围是（       ）

A． B．

C． D．

【答案】C

【分析】利用奇偶性可得，通过图像变换得出，根据正弦函数对称性得出且，通过求出此时的值域即可得出结果.

【详解】因为函数是奇函数，

所以，解得，即，

则，

向左平移个单位长度后，得到，

向上平移个单位长度，得到，

当时，，结合正弦函数对称性可知，

在有两个不相等实根，则且，

此时，实数m的取值范围是.

故选：C．

二、填空题

13．角α的顶点在坐标原点，始边与x轴的非负半轴重合，终边经过点P（1，2），则sin（π﹣α）的值是_____．

【答案】

【解析】计算sinα，再利用诱导公式计算得到答案.

【详解】由题意可得x＝1，y＝2，r，∴sinα，∴sin（π﹣α）＝sinα．

故答案为：．

【点睛】本题考查了三角函数定义，诱导公式，意在考查学生的计算能力.

14．已知数列{an}的前n项和为Sn，且满足an＝1+（n﹣1）d，5a2＝a8，则Sn＝__．

【答案】

【分析】由题意得5（1+d）＝1+7d，从而确定d＝2，再求数列的前n项和即可．

【详解】解：∵an＝1+（n﹣1）d，5a2＝a8，

∴5（1+d）＝1+7d，

解得，d＝2，

∴an＝1+2（n﹣1）＝2n﹣1，

故数列{an}为等差数列，

故Snn＝n2，

故答案为：n2．

15．中心在原点，焦点在y轴上的双曲线的一条渐近线经过点，则它的离心率为______．

【答案】

【分析】根据已知条件求得，由此求得双曲线的离心率.

【详解】由题意可设双曲线的标准方程为，

其渐近线方程为，则，

即，所以．

故答案为：

16．将一个边长为的正三角形沿其中线折成一个直二面角，则所得三棱锥的外接球的体积为_________.

【答案】

【分析】由垂直关系可知所求外接球即为以为长宽高的长方体的外接球，根据长方体外接球半径为体对角线的一半可求得外接球半径，由球的体积公式得到最终结果.

【详解】由题意得：，，，，即平面；

二面角为直二面角，，

则三棱锥的外接球即为以为长宽高的长方体的外接球，

又，

三棱锥的外接球半径，

三棱锥的外接球体积.

故答案为：.

三、解答题

17．已知等比数列的前项和为，且.

（1）求与；

（2）记，求数列的前项和.

【答案】（1），；（2）.

【分析】（1）利用可得数列的递推式，得其为等比数列，易得通项公式、求和；

（2）由（1）得，用错位相减法求和．

【详解】（1）由，得，

当时，，得；

当时，，得，

所以数列是以1为首项，2为公比的等比数列，

所以.

所以.

（2）由（1）可得，

则，

，

两式相减得，

所以

.

【点睛】（1）错位相减法适用于数列是由一个等差数列和一个等比数列对应项的乘积构成的数列的求和，求解的方法是等式两边乘等比数列的公比再错位相减，错位相减后化归为一个等比数列的求和；

（2）用错位相减法求和时，应注意两点：一是要善于识别题目类型，特别是等比数列公比为负数的情形；二是在写出“”与“”的表达式时应特别注意将两式“错项对齐”，以便下一步准确写出“”的表达式.

18．搪瓷制品是通过在金属坯体表面涂搪瓷釉而得到的，曾经是人们不可或缺的生活用品，厨房用具中的锅碗瓢盆、喝茶用到的杯子、洗脸用到的脸盆、婚嫁礼品等中都有它的影子，它浓缩了一个时代的记忆.某搪瓷设计公司新开发了一种新型复古搪瓷水杯，将其细分成6个等级，等级系数X依次为3，4，5，6，7，8.该公司将该款水杯的生产任务交给生产水平不同的M，N两厂，从N厂生产的该款搪瓷水杯中随机抽取30个，样本数据如图（1）所示.

(1)依据上（1）图，若从等级系数为7和8的搪瓷水杯中随机抽取2个，求这2个搪瓷水杯等级系数均为8的概率；

(2)如图（2）是5位网友对M，N两厂生产的搪瓷水杯的评分图，利用评分的平均数和标准差比较两厂生产的搪瓷水杯的评分情况，并说明理由.（参考数据：）

【答案】(1);

(2)答案见解析.

【分析】（1）列出基本事件，根据古典概型求解即可；

（2）根据所给数据，分别求出平均数及标准差，比较结果即可.

【详解】(1)（1）设样本中等级系数为7的搪瓷水杯为A，B，C，等级系数为8的搪瓷水杯为a，b，c，

则从中随机抽取2个，基本事件为，，，，，，，，，，，，，，，共15个.

其中2个搪瓷水杯等级系数均为8的基本事件为，，，共3个.

所以这2个搪瓷水杯等级系数均为8的概率为.

(2)N厂生产的搪瓷水杯的评分的平均数，

N厂生产的搪瓷水杯的评分的标准差

.

M厂生产的搪瓷水杯的评分的平均数，

M厂生产的搪瓷水杯的评分的标准差

.

综上，N厂生产的搪瓷水杯的评分的平均数较高；M厂生产的搪瓷水杯的评分的标准差较小，比较稳定.

19．如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．

（1）证明：平面平面；

（2）在线段上是否存在点，使得平面？说明理由．

【答案】（1）证明见解析

（2）存在，理由见解析

【详解】分析：（1）先证,再证，进而完成证明．

（2）判断出P为AM中点，，证明MC∥OP，然后进行证明即可．

详解：（1）由题设知，平面CMD⊥平面ABCD，交线为CD．

因为BC⊥CD，BC平面ABCD，所以BC⊥平面CMD，故BC⊥DM．

因为M为上异于C，D的点，且DC为直径，所以DM⊥CM．

又BC∩CM=C，所以DM⊥平面BMC．

而DM平面AMD，故平面AMD⊥平面BMC．

（2）当P为AM的中点时，MC∥平面PBD．

证明如下：连结AC交BD于O．因为ABCD为矩形，所以O为AC中点．

连结OP，因为P为AM 中点，所以MC∥OP．

MC平面PBD，OP平面PBD，所以MC∥平面PBD．

点睛：本题主要考查面面垂直的证明，利用线线垂直得到线面垂直，再得到面面垂直，第二问先断出P为AM中点，然后作辅助线，由线线平行得到线面平行，考查学生空间想象能力，属于中档题．

20．已知抛物线C：y2＝2px（0＜p＜8）的焦点为F点Q是抛物线C上的一点，且点Q的纵坐标为4，点Q到焦点的距离为5．

（1）求抛物线C的方程；

（2）设直线l不经过Q点且与抛物线交于A，B两点，QA，QB的斜率分别为K1，K2，若K1K2＝﹣2，求证：直线AB过定点，并求出此定点．

【答案】（1）y2＝4x；（2）见解析，定点（6，﹣4）

【分析】（1）由抛物线的性质到焦点的距离等于到准线的距离，设的坐标，由题意可得的值，进而求出抛物线的方程；

（2）设直线的方程与抛物线联立，求出两根之和及两根之积，进而求出直线，的斜率之积，由题意可得参数之间的关系，进而求出直线恒过的定点，注意直线不过，所以求出符合题意的定点的坐标．

【详解】解：（1）由题意，，直线方程为，由抛物线的性质，到焦点的距离等于到准线的距离，

由题意可得，解得或8，由题意可得，

所以抛物线的方程为：；

（2）由题意设直线的方程为：，设，，，，

联立直线与抛物线的方程可得，整理可得，

则，①

由（1）可得可得，

即，

即，

整理可得，

将①代入可得：，即，

所以，或，

即，或，

所以直线的方程为：，即恒过，

或者即恒过，

而由题意可得直线不过，

可证得直线 恒过定点．

【点睛】本题考查抛物线的性质，直线恒过定点的求法，属于中档题．

21．已知函数．

（I）若是的极值点，求的单调区间；

（II）求a的范围，使得恒成立．

【答案】（I）的单调增区间为，减区间为；（II）

【分析】（I）根据题意得出，求出a，进而由求得增区间，由求得减区间；

（II）根据题意将问题转化为时恒成立，设，求出，分类讨论参数a，得到，即可得到a的范围.

【详解】（I）函数的定义域为，，

因为是的极值点，所以，解得a=3，

当a=3时，，

令，得或；令，得，

所以函数的单调增区间为；单调减区间为.

（II）要使得恒成立，即时恒成立，

设，则，

当时，由得单调减区间为，由得单调增区间为，

故，得；

当时，由得单调减区间为，

由得单调增区间为，；此时，不合题意；

当时，在上单调递增，此时，不合题意；

当时，由得单调减区间为，由得单调增区间为，，此时，不合题意；

综上所述：时，恒成立.

22．在平面直角坐标系中，圆的参数方程为(为参数)，以为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为．

(1)求圆的普通方程及直线的直角坐标方程；

(2)若直线与圆的交点为，与轴的交点为，求的值．

【答案】(1)；

(2)

【分析】（1）由平方关系消参得圆的普通方程，由代入可得直线的直角坐标方程；

（2）求出，直线的倾斜角，写出直线的标准参数方程，代入圆的普通方程，利用参数的几何意义结合韦达定理求解．

【详解】(1)由方程消去参数得圆的普通方程为：

由得：

将代入得直线的直角坐标方程为：．

(2)由直线的直角坐标方程为：，故直线的倾斜角为

点坐标为：，所以直线的标准参数方程为：为参数．．

将直线的标准参数方程代入圆的普通方程得：

整理得：

由，设，两点对应的参数分别为：，

则，，且，异号．

．

23．已知实数，满足．

（1）若，求证：；

（2）设，求证：．

【答案】（1）证明见解析；（2）证明见解析．

【分析】（1）利用基本不等式可证得，再由基本不等式计算的最值，即可求证；

（2）利用反证法证明，假设，将已知条件平方可得，由已知条件可知可得，得出矛盾即可得证.

【详解】（1）时，，因为

所以

，

，

从而

当且仅当即时等号成立，

（2）假设，则由，知，故．

又由，得

但由知矛盾，

故不成立，所以．

【点睛】易错点点睛：利用基本不等式求最值或证明不等式时，必须满足一正、二定、三相等，验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.