2022届河南省南阳市第一中学校高三下学期第五次月考数学（理）试题含解析

2022届河南省南阳市第一中学校高三下学期第五次月考数学（理）试题

一、单选题

1．已知点，，，复数，在复平面内对应的向量分别是，，则复数（       ）

A． B． C． D．

【答案】C

【分析】根据复数的几何意义得到，，再根据复数代数形式的乘法法则计算可得；

【详解】解：依题意知，，于是，

故选：C.

2．设集合，为整数集，则集合子集的个数是（       ）

A．3 B．6 C．7 D．8

【答案】D

【分析】解不等式求得，然后求得，进而求得正确答案.

【详解】，所以，

所以,

所以子集的个数是.

故选：D

3．若“，使得”为真命题，则实数a的取值范围是（       ）

A． B．

C． D．

【答案】A

【分析】存在有解，先求值域，可知a的值.

【详解】解：若“，使得，

则要有解，

∵，

∴，

故选：A.

【点睛】本题考查三角函数的性质的应用、简易逻辑，属于基础题．

4．设函数满足，则（       ）

A． B．1 C． D．2

【答案】A

【分析】利用函数的导数的定义求解.

【详解】解：因为，

，

，

所以，

故选：A

5．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该几何体的体积为（       ）

A． B． C． D．

【答案】A

【解析】根据题意把三棱锥放入棱长为2的正方体中，得出三棱锥的形状，

结合图形，求出该三棱锥的体积．

【详解】解：根据题意，把三棱锥放入棱长为2的正方体中，是如图所示的三棱锥P﹣ABC，

∴三棱锥P﹣ABC的体积为：，

故选：A

【点睛】本题考查了利用三视图求空间几何体体积的应用问题，考查空间想象能力，是基础题．

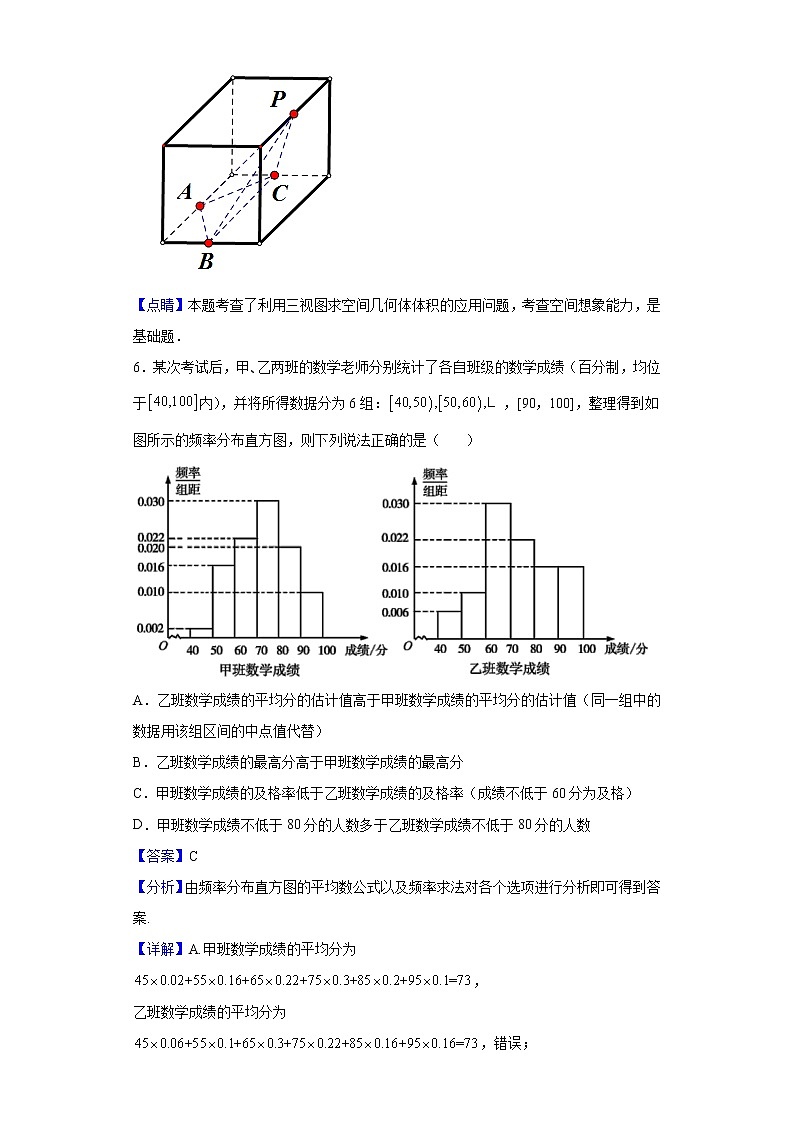
6．某次考试后，甲､乙两班的数学老师分别统计了各自班级的数学成绩（百分制，均位于内），并将所得数据分为6组：，[90，100]，整理得到如图所示的频率分布直方图，则下列说法正确的是（       ）

A．乙班数学成绩的平均分的估计值高于甲班数学成绩的平均分的估计值（同一组中的数据用该组区间的中点值代替）

B．乙班数学成绩的最高分高于甲班数学成绩的最高分

C．甲班数学成绩的及格率低于乙班数学成绩的及格率（成绩不低于60分为及格）

D．甲班数学成绩不低于80分的人数多于乙班数学成绩不低于80分的人数

【答案】C

【分析】由频率分布直方图的平均数公式以及频率求法对各个选项进行分析即可得到答案.

【详解】A.甲班数学成绩的平均分为，

乙班数学成绩的平均分为

，错误；

B.由频率分布直方图无法得到哪个班的最高分高，错误；

C.甲班数学成绩的及格率，乙班数学成绩的及格率，故甲班的低，正确；

D.甲乙两个班各班的总人数不知，故不能确定，错误；

故选：C

7．有以下四种变换方式：

① 向左平移个单位长度，再将每个点的横坐标缩短为原来的;

② 向右平移个单位长度，再将每个点的横坐标缩短为原来的;

③ 每个点的横坐标缩短为原来的，向右平移个单位长度;

④ 每个点的横坐标缩短为原来的，向左平移个单位长度;

其中能将的图像变换成函数的图像的是（       ）

A．①和③ B．①和④ C．②和④ D．②和③

【答案】B

【详解】试题分析：①“左加右减”向左平移可变为,再将每个点的横坐标缩短为原来的，变为；②变换为；③每个点的横坐标缩短为原来的，可变为，向右平移个单位长度，变为.④可变换为

.

【解析】三角函数图象变换.

8．已知能够被15整除，则的一个可能取值是（       ）

A．1 B．2 C．0 D．

【答案】D

【分析】利用二项展开式写出，由展开式可知需要能被15整除，结合选项可得答案.

【详解】,

75能够被15整除，要使原式能够被15整除，则需要能被15整除，将选项逐个检验可知的一个可能取值是，其他选项均不符合题意，

故选：D

9．瀑布是庐山的一大奇观，为了测量某个瀑布的实际高度，某同学设计了如下测量方案：有一段水平山道，且山道与瀑布不在同一平面内，瀑布底端与山道在同一平面内，可粗略认为瀑布与该水平山道所在平面垂直，在水平山道上A点位置测得瀑布顶端仰角的正切值为，沿山道继续走20m，抵达B点位置测得瀑布顶端的仰角为．已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为，则该瀑布的高度约为（       ）

A．60m B．90m C．108m D．120m

【答案】A

【分析】设瀑布顶端为P，底端为H，瀑布高为h，作出图形，根据条件可得，，由余弦定理可得答案.

【详解】解：如图，设瀑布顶端为P，底端为H，瀑布高为h，

该同学第一次测量时所处的位置为A，第二次测量时的位置为B，

由题意可知，，，且，

所以，，

在中，由余弦定理可知，，

即，解得．

故选：A．

10．已知函数，若对于任意的实数x，不等式恒成立，则实数a的取值范围为（       ）

A． B． C． D．

【答案】A

【分析】根据分段函数解析式画出函数图象，易知单调递增且关于对称，再将不等式转化为结合单调性求参数范围.

【详解】由题设，，图象如下：

所以，

又是R上的增函数，所以对恒成立，

所以，则，即．

故选：A．

11．已知双曲线的右焦点为，过点作双曲线的一条渐近线的垂线，垂足为.若直线与双曲线的另一条渐近线交于点，且满足（为坐标原点），则双曲线的离心率为（       ）

A． B． C． D．

【答案】A

【分析】由已知条件可得，设，可得，由已知向量关系可得，从而得到，即，由离心率公式可得答案.

【详解】双曲线右焦点到渐近线的距离为.

在中，，所以.

设，则，.

因为，所以，

所以，所以.在Rt中，，所以，即，即，所以.

故选:A.

12．若直线与曲线相切，直线与曲线相切，则的值为（       ）

A． B．1 C．e D．

【答案】B

【分析】设出切点，求出，，根据斜率列出方程，得到，，构造，利用函数单调性和图象特征，求出，从而求出答案.

【详解】设直线与曲线相切于点，

直线与曲线相切于点，

则，且，所以，

，且，所以，

令，，

当时，，单调递减，

当时，，单调递增，

且，，所以当时，，

因为，，即，

所以，

所以，故

故选：B

【点睛】对于不知道切点的切线方程问题，要设出切点，再根据斜率列出方程，进行求解.

二、填空题

13．等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线的准线交于A，B两点，；则C的实轴长为______．

【答案】

【详解】设等轴双曲线方程为，由题意可得抛物线的准线为，由，得，所以不妨设点，因为点在等轴双曲线上，所以，所以等轴双曲线的方程为，即，从而实轴长,

故答案为4.

【解析】双曲线、抛物线的有关概念和基本性质.

14．已知，，若，，则点C的坐标______．

【答案】

【分析】根据向量平行的坐标表示和向量垂直的坐标表示列方程可求点C的坐标.

【详解】设点的坐标为，则

，

因为，，

所以

因为，，

所以，，

所以，

所以点C的坐标为，

故答案为：.

15．在中，角所对的边分别为，且满足，则的最大值是__________.

【答案】0.6

【分析】由余弦定理结合基本不等式可得，从而得到的最大值.

【详解】由得：

故，

当且仅当时取等号，由于，故，

则，则，

即的最大值是

故答案为：

16．如图，在四面体中，，，､分别是､的中点.若用一个与直线垂直，且与四面体的每个面都相交的平面去截该四面体，由此得到一个多边形截面，则下面的说法中正确的有___________.

①，

②四面体外接球的表面积为.

③异面直线与所成角的正弦值为

④多边形截面面积的最大值为.

【答案】①②④

【分析】连接，进而根据线面垂直得线线垂直可判断①；将其补成长方体，转为为求长方体的外接球表面积可判断②；结合②建立空间直角坐标系，利用坐标法求解即可判断③；根据题意，证明截面为平行四边形，且，由可判断④.

【详解】解：对于①，连接，因为，､分别是､的中点，所以，，因为，所以平面,平面，所以，，故正确；

对于②，该几何体可以在如图2的长方体中截出，设长方体的长宽高分别为，

则，所以，即长方体的体对角线的长度为，

所以四面体的外接球即为该长方体的外接球，半径满足，

所以四面体外接球的表面积为，故正确；

对于③，由②得，如图3，以点为坐标原点，建立空间直角坐标系，则，,，，故，所以异面直线与所成角的余弦值为，故错误；

对于④，如图4，设平面与分别交于，

，，则由线面平行的性质可得，则,

同理，，所以截面为平行四边形，

可得，

则，

设异面直线和所成角为，由③的讨论可得异面直线和所成角为，

所以，

则可得，当且仅当时等号成立，故正确.

故答案为：①②④

【点睛】本题考查空间几何体的截面问题，内接外接球问题，线面垂直，线线垂直等位置关系，考查运算求解能力，直观想象能力，是难题.本题解题的关键在于将该几何体放置于长方体中，利用长方体的几何性质求解.

三、解答题

17．“学习强国”学习平台是由中共中央宣传部主管，以习近平新时代中国特色社会主义思想和党的十九大精神为主要内容，立足全体党员､面向全社会的优质平台，其中的“挑战答题”更是趣味盎然､引人入胜“挑战答题”规则为：（1）挑战开始后，挑战者依次回答界面中出现的问题，答对就继续下一题，答错有两种选择：①结束本局，挑战结束；②通过分享界面复活本局，复活之后可继续本次挑战，且答对题数可累加；（2）答对5题或5题以上均为挑战成功，可获得6分，否则无积分可得；（3）每次挑战，通过分享界面复活的机会只有一次.

(1)如果甲对“挑战答题”中的每一道题回答正确的概率均为，且各题是否回答正确互不影响，求甲挑战一次就获得成功的概率；

(2)假设乙挑战一次获得成功的概率为，他在一周内（天）每天都挑战一次，且每次挑战是否成功互不影响.设乙在一周内挑战答题总得分为，求的分布列及数学期望.

【答案】(1)

(2)分布列见解析，数学期望为

【分析】（1）根据相互独立事件和互斥事件的概率公式计算可得；

（2）设乙在一周内挑战成功的次数为，依题意可得，且，根据二项分布的概率公式求出所对应的概率，即可得到分布列，再根据二项分布的期望公式及期望的性质计算可得；

【详解】(1)解：记事件为前5题都回答正确；

记事件为前5题有且只有1题回答错误，其余回答正确，且第6题回答正确.

记挑战一次获得成功为事件，则事件包含两个事件，且互斥，所以.

因为甲对挑战答题中的每一道题回答正确的概率均为，

所以.

故甲挑战一次就获得成功的概率为.

(2)解：设乙在一周内挑战成功的次数为，

由题意知，服从二项分布，即.

因为，所以，

，

，

，

，

所以的分布列为：

因为，

所以

18．已知三棱锥（如图一）的平面展开图（如图二）中，四边形为边长等于的正方形，和均为正三角形，在三棱锥中：

图一

图二

(1)证明：平面平面；

(2)若点在棱上运动，当直线与平面所成的角最大时，求二面角的余弦值.

【答案】(1)证明见解析

(2)

【分析】（1）设的中点为，连接，证明平面，从而可证明结论.

（2）先证明平面，得到是直线与平面所成的角，进一步得到是的中点时，最大，然后以，，所在直线分别为轴，轴，轴建立空间坐标系，利用向量法求解即可.

【详解】(1)设的中点为，连接，由题意，得，，

.因为在中，，为的中点，所以，因为在中，，，，则，所以，

因为，平面，

所以平面，因为平面，所以平面平面.

(2)由（1）知，，，且 ，则平面，

连接,所以是直线与平面所成的角，且，

所以当最短时，即时，最大.

由四边形为边长等于的正方形，则为等腰直角三角形，即

所以即是的中点时，最大.

由平面，，所以，，

于是以，，所在直线分别为轴，轴，轴建立如图示空间直角坐标系

则，，，，，，

所以，，.

设平面的法向量为，则由得：.

令，得，，即.

设平面的法向量为，

由得：，令，得，，即.

.由图可知，二面角的余弦值为.

19．已知数列满足，且对于任意成立.

(1)证明：是等比数列；

(2)若等差数列的前项和为，且满足，是否存在正整数，对于任意大于的正整数，均有成立？若存在，写出一个满足条件的，并证明；若不存在，请说明理由.

【答案】(1)证明见解析；

(2)存在，，证明见解析.

【分析】（1）对已知递推公式进行变形，结合等比数列的定义进行证明即可；

（2）根据等差数列前项和的性质，结合等差数列的单调性进行求解即可.

【详解】(1)由题目条件整理可得：，

且，

因此是首项为，公比为的等比数列；

(2)由（1）知，，

所以，

由条件可知：因为，

，又因为，可得.

且数列单调递増，

因此时，.取即可.

20．设函数．

(1)当a =1时，求曲线在点处的切线方程；

(2)若在x =2处取得极小值，求a的取值范围．

【答案】(1)

(2)

【分析】（1）由导数的几何意义求解

（2）由导数分类讨论函数的单调性后求解

【详解】(1)当时，得：     ∴，

∴，，

即曲线在处的切线的斜率，所求切线方程为．

(2)因为，

所以，

设，

①时，

当时，，，

当时，，，

则在单调递增，在单调递减；

所以在处存在极大值，与题目矛盾，

②时，令解得，，

若，则 ，

当时，，

当时，，，

则在单调递增，在单调递减；

所以在处存在极大值，与题目矛盾，

若，，即，

当时，，，

当时，，，

则在单调递减，在单调递增；

所以在处存在极小值，满足条件，

若，即，

当时，，，

当时，，，

则在单调递增，单调递减；

所以在处存在极大值，与题目矛盾，

综上所述：的取值范围为

21．已知椭圆的离心率为，短轴长为4；

(1)求C的方程；

(2)过点作两条相互垂直的直线上和，直线与C相交于两个不同点A，B，在线段上取点Q，满足，直线交y轴于点R，求面积的最小值．

【答案】(1)；

(2)1.

【分析】（1）由题可得，即得；

（2）由题可设的方程为，利用韦达定理法可得，进而可得，然后利用面积公式及基本不等式即求.

【详解】(1)由题可得，

∴，

∴椭圆C的方程为；

(2)由题可知直线的斜率存在且不为0，设直线的方程为，

，

由，可得，

由，可得，或，

∴，

由及四点共线，知，

∴，

则，

∵和相互垂直，则的方程为，令，得，

∴，，

∴面积为，

当且仅当，即等号成立，

所以面积的最小值为1.

22．在平面直角坐标系中，曲线的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．

(1)求的普通方程和的直角坐标方程；

(2)过上一点P作的一条切线l，切点为Q，当最小时，求△外接圆的参数方程．

【答案】(1)，

(2)（为参数）

【分析】（1）消去参数即可得到的普通方程，利用极坐标和直角坐标的转化关系即可得到的直角坐标方程；

（2）由已知条件得,则当最小，也最小，最小时，，即可求出直线的方程，利用几何性质即可求出△外接圆的参数方程.

【详解】(1)由消去t得的普通方程为，

因为，

所以，

所以，

即的直角坐标方程为．

(2)由圆的切线的性质可知，当时，最小，也最小．

此时直线的斜率为，因为，所以直线的方程为．

由，得，

所以的中点坐标为，，

所以△外接圆的参数方程为（为参数）．

23．已知函数．

(1)若，解关于的不等式；

(2)若对，不等式恒成立，求实数的取值范围．

【答案】(1)

(2)

【分析】（1）分别在、和的情况下，去掉绝对值符号，解不等式求得结果；

（2）将不等式变为，由此可解得，分别求得的最小值和的最大值，由此可得的取值范围.

【详解】(1)当时，；

当时，，解得：；

当时，，解得：（舍）；

当时，，解得：；

的解集为：.

(2)当时，，，

，解得：，

，，，

即实数的取值范围为.