人教版高考数学一轮复习第6章数列第1节数列的概念与简单表示法学案理含解析

这是一份人教版高考数学一轮复习第6章数列第1节数列的概念与简单表示法学案理含解析，共8页。学案主要包含了疑误辨析，走进教材，易错自纠等内容，欢迎下载使用。
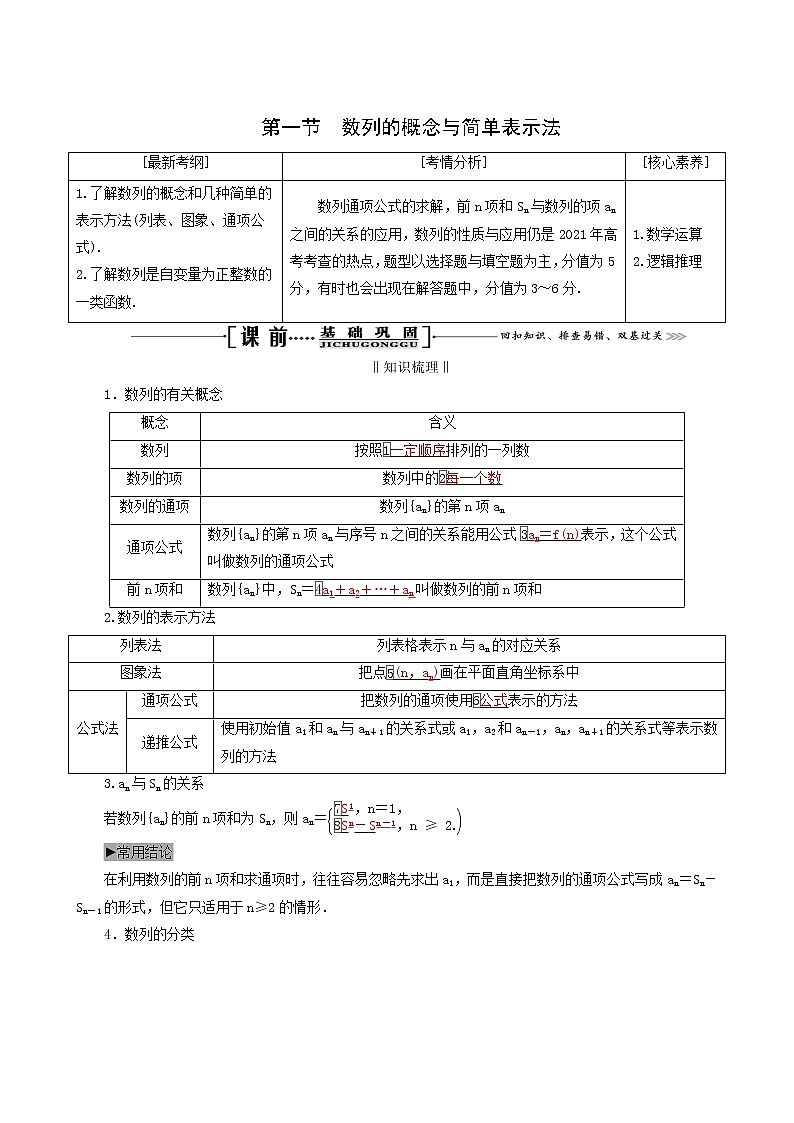
第一节　数列的概念与简单表示法[最新考纲][考情分析][核心素养]1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).2.了解数列是自变量为正整数的一类函数.　　数列通项公式的求解，前n项和Sn与数列的项an之间的关系的应用，数列的性质与应用仍是2021年高考考查的热点，题型以选择题与填空题为主，分值为5分，有时也会出现在解答题中，分值为3～6分.1.数学运算2.逻辑推理‖知识梳理‖1．数列的有关概念概念含义数列按照一定顺序排列的一列数数列的项数列中的每一个数数列的通项数列{an}的第n项an通项公式数列{an}的第n项an与序号n之间的关系能用公式an＝f(n)表示，这个公式叫做数列的通项公式前n项和数列{an}中，Sn＝a1＋a2＋…＋an叫做数列的前n项和2.数列的表示方法列表法列表格表示n与an的对应关系图象法把点(n，an)画在平面直角坐标系中公式法通项公式把数列的通项使用公式表示的方法递推公式使用初始值a1和an与an＋1的关系式或a1，a2和an－1，an，an＋1的关系式等表示数列的方法3.an与Sn的关系若数列{an}的前n项和为Sn，则an＝►常用结论在利用数列的前n项和求通项时，往往容易忽略先求出a1，而是直接把数列的通项公式写成an＝Sn－Sn－1的形式，但它只适用于n≥2的情形．4．数列的分类►常用结论1．数列是一种特殊的函数，数列的单调性、周期性在求值时常常用到. 2．在数列{an}中，若an最大，则若an最小，则‖基础自测‖一、疑误辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)．(1)相同的一组数按不同顺序排列时都表示同一个数列．(　　)(2)所有数列的第n项都能使用公式表达．(　　)(3)根据数列的前几项归纳出数列的通项公式可能不止一个．(　　)(4)1，1，1，1，…，不能构成一个数列．(　　)(5)任何一个数列不是递增数列，就是递减数列．(　　)(6)如果数列{an}的前n项和为Sn，则对∀n∈N*，都有an＋1＝Sn＋1－Sn.(　　)答案：(1)×　(2)×　(3)√　(4)×　(5)×　(6)√二、走进教材2．(必修5P33A4改编)在数列{an}中，a1＝1，an＝1＋(n≥2)，则a5等于(　　)A． B．C． D．答案：D3．(必修5P33A5改编)根据下面的图形及相应的点数，写出点数构成的数列的一个通项公式an＝________．答案：5n－4三、易错自纠4．已知数列{an}的通项公式为an＝n2－8n＋15，则(　　)A．3不是数列{an}中的项B．3只是数列{an}中的第2项C．3只是数列{an}中的第6项D．3是数列{an}中的第2项或第6项解析：选D　令an＝3，即n2－8n＋15＝3，解得n＝2或n＝6，故3是数列{an}中的第2项或第6项．5．已知数列{an}的前n项和为Sn＝3＋2n，则数列{an}的通项公式为______________．解析：当n＝1时，a1＝S1＝3＋2＝5；当n≥2时，an＝Sn－Sn－1＝3＋2n－(3＋2n－1)＝2n－2n－1＝2n－1.因为当n＝1时，不符合an＝2n－1，所以数列{an}的通项公式为an＝答案：an＝6．已知数列{an}的前n项和Sn＝2n2＋n，则an＝________．解析：当n≥2时，an＝Sn－Sn－1＝2n2＋n－2(n－1)2－(n－1)＝4n－1.当n＝1时，a1＝S1＝3＝4×1－1，也满足上式，故an＝4n－1.答案：4n－1|题组突破|1．已知数列{an}的前n项和为Sn＝n2－2n＋2，则数列{an}的通项公式为(　　)A．an＝2n－3 B．an＝2n＋3C．an＝ D．an＝解析：选C　当n＝1时，a1＝S1＝1；当n≥2时，an＝Sn－Sn－1＝2n－3.由于当n＝1时，a1的值不适合n≥2的解析式，故选C．2．已知数列{an}的前n项和Sn＝2an－1，则满足≤2的正整数n的集合为(　　)A．{1，2，3} B．{2，3，4}C．{1，2，3，4} D．{1，2，3，4，5}解析：选C　因为Sn＝2an－1，所以当n≥2时，Sn－1＝2an－1－1，两式相减得an＝2an－2an－1，整理得an＝2an－1.又a1＝2a1－1，所以a1＝1，故an＝2n－1.又≤2，即2n－1≤2n，所以有n∈{1，2，3，4}．3．(2019届潍坊模拟)已知数列{an}的前n项和Sn＝an＋，则{an}的通项公式an＝________．解析：当n＝1时，a1＝S1＝a1＋，∴a1＝1；当n≥2时，an＝Sn－Sn－1＝an－an－1，∴＝－.∴数列{an}为首项a1＝1，公比q＝－的等比数列，故an＝.答案：►名师点津已知Sn求an的3个步骤(1)先利用a1＝S1求出a1.(2)用n－1替换Sn中的n得到一个新的关系，利用an＝Sn－Sn－1(n≥2)便可求出当n≥2时an的表达式．(3)对n＝1时的结果进行检验，看是否符合n≥2时an的表达式，如果符合，则可以把数列的通项公式合写；如果不符合，则应该分n＝1与n≥2两段来写．——多维探究●命题角度一　形如an＋1－an＝f(n)，求an【例1】　(2019届郑州模拟)设数列{an}满足a1＝1，且an＋1－an＝n＋1(n∈N*)，则数列{an}的通项公式为________．[解析]　由题意得a2－a1＝2，a3－a2＝3，…，∴an－an－1＝n(n≥2)．以上各式相加，得an－a1＝2＋3＋…＋n＝＝.∵a1＝1，∴an＝(n≥2)．∵当n＝1时也满足此式，∴an＝.[答案]　an＝►名师点津对于形如an＋1－an＝f(n)的递推关系的递推数列，即数列相邻两项之差是一个关于n的函数式，可以直接对等式两边求和进行解答，也可写为an＝(an－1－an－2)＋…＋(a2－a1)＋a1的形式．●命题角度二　形如＝f(n)，求an【例2】　在数列{an}中，a1＝1，an＝an－1(n≥2，n∈N*)，则数列{an}的通项公式为________．[解析]　∵an＝an－1(n≥2)，∴an－1＝an－2，an－2＝an－3，…，a2＝a1.以上各式相乘得，an＝a1···…·＝＝.当n＝1时，a1＝1，符合上式，∴an＝.[答案]　an＝►名师点津对于形如＝f(n)的递推关系的递推数列，即数列相邻两项之商是一个关于n的函数式，可以直接对等式两边求积解答，也可写为an＝··…··a1的形式．●命题角度三　形如an＋1＝pan＋q(p≠0且p≠1，q≠0)，求an【例3】　(2019届青岛模拟)已知数列{an}满足a1＝1，an＋1＝3an＋2(n∈N*)，则数列{an}的通项公式为____________．[解析]　∵an＋1＝3an＋2，∴an＋1＋1＝3(an＋1)，∴＝3，又∵a1＋1＝2.∴数列{an＋1}是以2为首项，3为公比的等比数列．∴an＋1＝2·3n－1，∴an＝2·3n－1－1.[答案]　an＝2·3n－1－1►名师点津对于形如an＋1＝pan＋q(p≠0且p≠1，q≠0)的递推关系的递推数列，即数列相邻的次数都是一次，尾巴上有一个常数，求此类数列的通项公式，通常采用待定系数法将其转化为an＋1＋k＝p(an＋k)求解．●命题角度四　形如an＋1＝(A，B，C为常数)，求an【例4】　已知在数列{an}中，a1＝1，an＋1＝(n∈N*)，则数列{an}的通项公式an＝________．[解析]　因为an＋1＝，a1＝1，所以an≠0，所以＝＋，即－＝.又a1＝1，所以＝1，所以是以1为首项，为公差的等差数列．所以＝1＋(n－1)×＝＋.所以an＝.[答案]　►名师点津形如an＋1＝(A，B，C为常数)的数列，将其变形为＝·＋.①若A＝C，则是等差数列，且公差为，可直接用公式求通项；②若A≠C，则采用待定系数法，构造新数列求解．|跟踪训练|1．(累加法)已知在数列{an}中，a1＝3，an＋1＝an＋，则通项公式an＝________．解析：原递推公式可化为an＋1＝an＋－，则当n≥2时，a2＝a1＋1－，a3＝a2＋－，a4＝a3＋－，…，an－1＝an－2＋－，an＝an－1＋－，累计相加得，an＝a1＋1－，故an＝4－.又当n＝1时，也符合上式，∴an＝4－.答案：4－2．(累乘法)已知a1＝2，an＋1＝2nan，则数列{an}的通项公式an＝________．解析：∵an＋1＝2nan，∴＝2n.当n≥2时，an＝··…··a1＝2n－1·2n－2·…·2·2＝2.又a1＝2也符合上式，∴an＝2.答案：23．(待定系数法)已知数列{an}中，a1＝3，且点Pn(an，an＋1)(n∈N*)在直线4x－y＋1＝0上，则数列{an}的通项公式为______________．解析：因为点Pn(an，an＋1)(n∈N*)在直线4x－y＋1＝0上，所以4an－an＋1＋1＝0.所以an＋1＋＝4.因为a1＝3，所以a1＋＝.故数列是首项为，公比为4的等比数列．所以an＋＝×4n－1.故数列{an}的通项公式为an＝×4n－1－.答案：an＝×4n－1－4．(取倒数法)已知数列{an}满足a1＝1，an＋1＝(n∈N*)，若bn＋1＝(n－2λ)·(n∈N*)，b1＝－λ，且数列{bn}是递增数列，则实数λ的取值范围是________．解析：由an＋1＝，得＝1＋，所以＋1＝2，故是首项为＋1＝2，公比为2的等比数列，所以＋1＝2n.因为bn＋1＝(n－2λ)·＝(n－2λ)·2n，b1＝－λ，且数列{bn}是递增数列，所以解得所以λ<.答案：数列是特殊的函数，数列中项的最值问题的求解与判断多借用函数的单调性或图象来解决．【例】　(2019届上饶调研)已知在数列{an}中，an＝1＋(n∈N*，a∈R且a≠0)．(1)若a＝－7，求数列{an}中的最大项和最小项的值；(2)若对任意的n∈N*，都有an≤a6成立，求a的取值范围．[解]　(1)∵an＝1＋(n∈N*，a∈R，且a≠0)，又a＝－7，∴an＝1＋(n∈N*)．结合函数f(x)＝1＋的单调性，可知1>a1>a2>a3>a4，a5>a6>a7>…>an>1(n∈N*)．∴数列{an}中的最大项为a5＝2，最小项为a4＝0.(2)an＝1＋＝1＋，已知对任意的n∈N*，都有an≤a6成立，结合函数f(x)＝1＋的单调性，可知5<<6，即－10<a<－8.►名师点津数列{an}的最大(小)项的求法(1)函数法：借助数列的单调性或图象来解决．(2)利用不等式组(n≥2)找到数列的最大项；利用不等式组(n≥2)找到数列的最小项．|跟踪训练|已知数列{an}满足an＝若对任意的n∈N*都有an>an＋1，则实数a的取值范围是(　　)A． B．C． D．解析：选B　因为an>an＋1恒成立，又当n≥6时，{an}为等比数列，所以0<a<1.若0<a≤，则当n<6时，不满足题意；若<a<1，则当n≥6时，an>an＋1，当n<6时，数列{an}单调递减．又an>an＋1对任意的n∈N*恒成立，所以a6<a5，即a<×5＋1，解得a<，所以<a<，故选B．