人教版高考数学一轮复习第9章解析几何第4节直线与圆圆与圆的位置关系学案理含解析

这是一份人教版高考数学一轮复习第9章解析几何第4节直线与圆圆与圆的位置关系学案理含解析，共7页。学案主要包含了疑误辨析，走进教材，易错自纠等内容，欢迎下载使用。
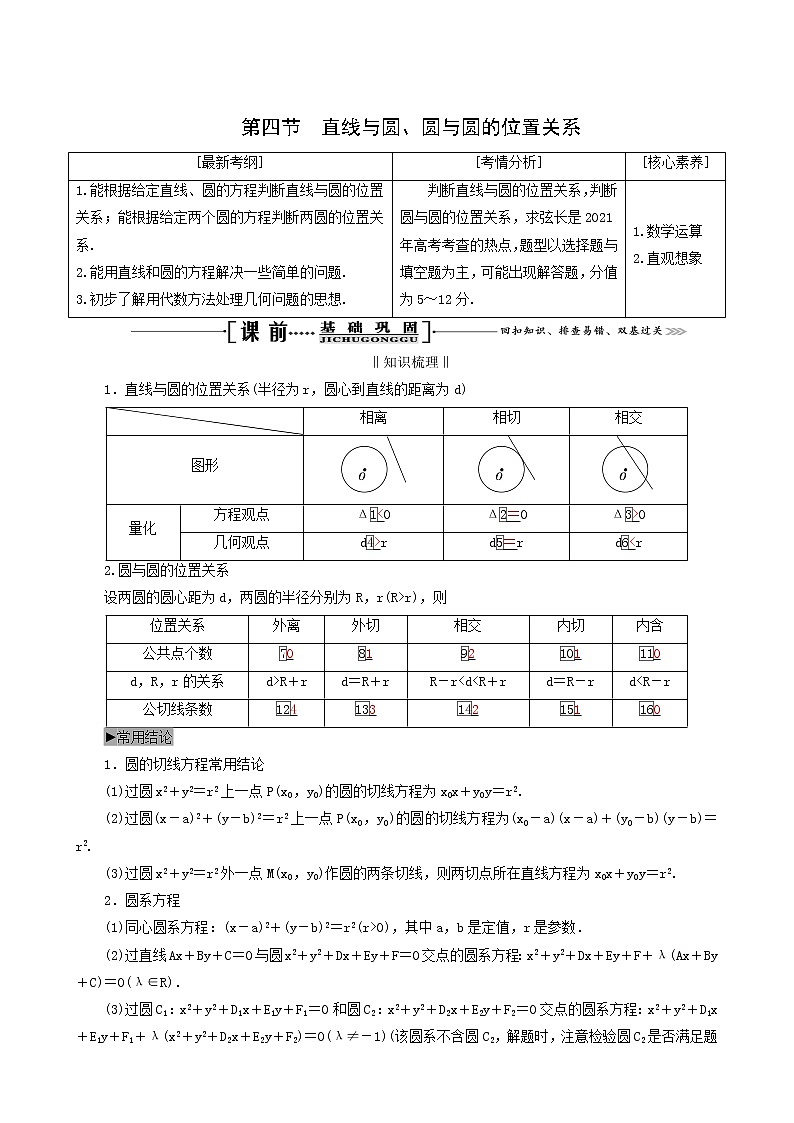
第四节　直线与圆、圆与圆的位置关系[最新考纲][考情分析][核心素养]1.能根据给定直线、圆的方程判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆的位置关系.2.能用直线和圆的方程解决一些简单的问题.3.初步了解用代数方法处理几何问题的思想.　　判断直线与圆的位置关系，判断圆与圆的位置关系，求弦长是2021年高考考查的热点，题型以选择题与填空题为主，可能出现解答题，分值为5～12分.1.数学运算2.直观想象‖知识梳理‖1．直线与圆的位置关系(半径为r，圆心到直线的距离为d) 相离相切相交图形量化方程观点Δ<0Δ＝0Δ>0几何观点d>rd＝rd<r2.圆与圆的位置关系设两圆的圆心距为d，两圆的半径分别为R，r(R>r)，则位置关系外离外切相交内切内含公共点个数01210d，R，r的关系d>R＋rd＝R＋rR－r<d<R＋rd＝R－rd<R－r公切线条数43210►常用结论1．圆的切线方程常用结论(1)过圆x2＋y2＝r2上一点P(x0，y0)的圆的切线方程为x0x＋y0y＝r2.(2)过圆(x－a)2＋(y－b)2＝r2上一点P(x0，y0)的圆的切线方程为(x0－a)(x－a)＋(y0－b)(y－b)＝r2.(3)过圆x2＋y2＝r2外一点M(x0，y0)作圆的两条切线，则两切点所在直线方程为x0x＋y0y＝r2.2．圆系方程(1)同心圆系方程：(x－a)2＋(y－b)2＝r2(r>0)，其中a，b是定值，r是参数．(2)过直线Ax＋By＋C＝0与圆x2＋y2＋Dx＋Ey＋F＝0交点的圆系方程：x2＋y2＋Dx＋Ey＋F＋λ(Ax＋By＋C)＝0(λ∈R)．(3)过圆C1：x2＋y2＋D1x＋E1y＋F1＝0和圆C2：x2＋y2＋D2x＋E2y＋F2＝0交点的圆系方程：x2＋y2＋D1x＋E1y＋F1＋λ(x2＋y2＋D2x＋E2y＋F2)＝0(λ≠－1)(该圆系不含圆C2，解题时，注意检验圆C2是否满足题意，以防漏解)．‖基础自测‖一、疑误辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)．(1)“k＝1”是“直线x－y＋k＝0与圆x2＋y2＝1相交”的必要不充分条件．(　　)(2)如果两个圆的方程组成的方程组只有一组实数解，则两圆外切．(　　)(3)如果两圆的圆心距小于两圆的半径之和，则两圆相交．(　　)(4)圆C1：x2＋y2＋2x＋2y－2＝0与圆C2：x2＋y2－4x－2y＋1＝0的公切线有且仅有2条．(　　)答案：(1)×　(2)×　(3)×　(4)√二、走进教材2．(必修2P132A5改编)直线l：3x－y－6＝0与圆x2＋y2－2x－4y＝0相交于A，B两点，则|AB|＝________．答案：3．(必修2P133A9改编)圆x2＋y2－4＝0与圆x2＋y2－4x＋4y－12＝0的公共弦长为________．答案：2三、易错自纠4．(2019届惠州调研)圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为(　　)A．内切 B．相交C．外切 D．相离解析：选B　由题意知，两圆的圆心距离为＝，两圆的半径之差为1，半径之和为5，又1<<5，所以两圆相交．5．直线4x－3y＝0与圆(x－1)2＋(y－3)2＝10相交所得的弦长为(　　)A．6 B．3C．6 D．3解析：选A　设直线4x－3y＝0与圆(x－1)2＋(y－3)2＝10相交所得的弦为AB．∵圆的半径r＝，圆心到直线的距离d＝＝＝1，∴弦长|AB|＝2×＝2＝2×3＝6.故选A．6．已知直线l经过点P(－4，－3)，且被圆(x＋1)2＋(y＋2)2＝25截得的弦长为8，则直线l的方程是________________．解析：由已知条件知圆心为(－1，－2)，半径r＝5，弦长m＝8.设弦心距是d，则由勾股定理得r2＝d2＋，即25＝d2＋16，解得d＝3.若l的斜率不存在，则直线l的方程为x＝－4，圆心到直线的距离是3，符合题意．若l的斜率存在，设为k，则直线l的方程为y＋3＝k(x＋4)，即kx－y＋4k－3＝0，则d＝＝3，即9k2－6k＋1＝9k2＋9，解得k＝－，则直线l的方程为4x＋3y＋25＝0.所以直线l的方程是x＋4＝0或4x＋3y＋25＝0.答案：x＋4＝0或4x＋3y＋25＝0|题组突破|1．(2019届西安模拟)直线(a＋1)x＋(a－1)y＋2a＝0(a∈R)与圆x2＋y2－2x＋2y－7＝0的位置关系是(　　)A．相切 B．相交C．相离 D．不确定解析：选B　由(a＋1)x＋(a－1)y＋2a＝0(a∈R)整理得x－y＋a(x＋y＋2)＝0，则由解得x＝－1，y＝－1，即直线(a＋1)x＋(a－1)y＋2a＝0(a∈R)过定点(－1，－1)．又(－1)2＋(－1)2－2×(－1)＋2×(－1)－7＝－5<0，则点(－1，－1)在圆x2＋y2－2x＋2y－7＝0的内部，故直线(a＋1)x＋(a－1)y＋2a＝0(a∈R)与圆x2＋y2－2x＋2y－7＝0相交．2．已知圆M：x2＋y2－2ay＝0(a>0)截直线x＋y＝0所得线段的长度是2，则圆M与圆N：(x－1)2＋(y－1)2＝1的位置关系是(　　)A．内切 B．相交C．外切 D．相离解析：选B　由题知圆M：x2＋(y－a)2＝a2(a>0)，圆心(0，a)到直线x＋y＝0的距离d＝，所以2＝2，解得a＝2，所以圆M，圆N的圆心距|MN|＝，两圆半径之差为1，半径之和为3，1<<3，故两圆相交．►名师点津1．判断直线与圆的位置关系的一般方法几何法圆心到直线的距离与圆半径比较大小，即可判断直线与圆的位置关系．这种方法的特点是计算量较小代数法将直线方程与圆方程联立方程组，再将二次方程组转化为一元二次方程，该方程解的情况即对应直线与圆的位置关系．这种方法具有一般性，适合于判断直线与圆锥曲线的位置关系2.圆与圆位置关系问题的解题策略(1)判断两圆的位置关系时常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法．(2)若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差消去x2，y2项得到．【例1】　(2019届广东七校联考)已知点P(3，＋2)，Q(4，3)，圆M：(x－1)2＋(y－2)2＝9.(1)求过点P的圆M的切线方程；(2)求过点Q的圆M的切线方程以及切线长．[解]　由题意知圆M的圆心为M(1，2)，半径r＝3.(1)∵(3－1)2＋(＋2－2)2＝9，∴点P在圆M上．又kPM＝＝，∴切线的斜率k＝－＝－.∴过点P的圆M的切线方程为y－(＋2)＝－(x－3)，即2x＋y－11－2＝0.(2)∵(4－1)2＋(3－2)2＝9＋1＝10>9，∴点Q在圆M外部．①当过点Q的直线的斜率不存在时，直线的方程为x＝4，即x－4＝0.又知点M(1，2)到直线x－4＝0的距离d＝4－1＝3＝r，∴直线x－4＝0符合题意．②当过点Q的直线的斜率存在时，设直线方程为y－3＝k(x－4)，即kx－y－4k＋3＝0，则圆心M到直线的距离d＝＝3，即|1－3k|＝3，解得k＝－，∴切线方程为－x－y－4×＋3＝0，即4x＋3y－25＝0.综上可知，过点Q的圆M的切线方程为x＝4或4x＋3y－25＝0.∵|QM|＝＝，∴过点Q的圆M的切线长为＝＝1.►名师点津1．求过圆上的一点(x0，y0)的切线方程的方法先求切点与圆心连线的斜率k，若k不存在，则结合图形可直接写出切线方程为y＝y0；若k＝0，则结合图形可直接写出切线方程为x＝x0；若k存在且k≠0，则由垂直关系知切线的斜率为－，由点斜式可写出切线方程．2．求过圆外一点(x0，y0)的圆的切线方程的2种方法几何法当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即kx－y＋y0－kx0＝0.由圆心到直线的距离等于半径，即可求出k的值，进而写出切线方程代数法当斜率存在时，设为k，则切线方程为y－y0＝k(x－x0)，即y＝kx－kx0＋y0，代入圆的方程，得到一个关于x的一元二次方程，由Δ＝0，求得k，切线方程即可求出[提醒]　当点(x0，y0)在圆外时，一定要注意斜率不存在的情况．|跟踪训练|1．已知圆C：x2＋y2－2x－4y＋3＝0.(1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程；(2)从圆C外一点P(x1，y1)向该圆引一条切线，切点为M，O为坐标原点，且有|PM|＝|PO|，求|PM|的最小值．解：(1)将圆C的方程化为标准方程得(x－1)2＋(y－2)2＝2，即C(1，2)，半径为.当直线在两坐标轴上的截距为零时，设直线方程为y＝kx(k≠0)，由直线与圆相切得＝，解得k＝－2±，所以切线方程为y＝(－2＋)x或y＝(－2－)x.当直线在两坐标轴上的截距不为零时，设直线方程为x＋y－a＝0，由直线与圆相切得＝，解得a＝1或a＝5，所以切线方程为x＋y－1＝0或x＋y－5＝0.综上，所求的切线方程为y＝(－2＋)x或y＝(－2－)x或x＋y－1＝0或x＋y－5＝0.(2)由|PM|＝|PO|得(x1－1)2＋(y1－2)2－2＝x＋y，即2x1＋4y1－3＝0，即点P在直线l：2x＋4y－3＝0上，所以|PM|min＝|PO|min＝＝.【例2】　已知⊙H被直线x－y－1＝0，x＋y－3＝0分成面积相等的四部分，且截x轴所得线段的长为2.(1)求⊙H的方程；(2)若存在过点P(a，0)的直线与⊙H相交于M，N两点，且|PM|＝|MN|，求实数a的取值范围．[解]　(1)设⊙H的方程为(x－m)2＋(y－n)2＝r2(r>0)，因为⊙H被直线x－y－1＝0，x＋y－3＝0分成面积相等的四部分，所以圆心H(m，n)一定是两直线x－y－1＝0，x＋y－3＝0的交点，易得交点坐标为(2，1)，所以m＝2，n＝1.又⊙H截x轴所得线段的长为2，所以r2＝1＋n2＝2，所以⊙H的方程为(x－2)2＋(y－1)2＝2.(2)设N(x0，y0)，由题意易知点M是PN的中点，所以M.因为M，N两点均在⊙H上，所以(x0－2)2＋(y0－1)2＝2， ①＋＝2，即(x0＋a－4)2＋(y0－2)2＝8. ②若记⊙I为(x＋a－4)2＋(y－2)2＝8，由①②知⊙H与⊙I有公共点，从而2－≤|HI|≤2＋，即≤≤3，整理可得2≤a2－4a＋5≤18，解得2－≤a≤1或3≤a≤2＋，所以实数a的取值范围是[2－，1]∪[3，2＋ ]．►名师点津有关弦长问题的2种求法几何法直线被圆截得的半弦长，弦心距d和圆的半径r构成直角三角形，即r2＝＋d2代数法联立直线方程和圆的方程，消元转化为关于x的一元二次方程，由根与系数的关系即可求得弦长|AB|＝|x1－x2|＝或|AB|＝|y1－y2|＝  |跟踪训练|2．(2019届河北石家庄质检)已知a∈R且为常数，圆C：x2＋2x＋y2－2ay＝0，过圆C内一点(1，2)的直线l与圆C相交于A，B两点．当∠ACB最小时，直线l的方程为2x－y＝0，则a的值为(　　)A．2 B．3C．4 D．5解析：选B　将圆的方程化为标准方程，得(x＋1)2＋(y－a)2＝1＋a2，圆心为C(－1，a)，当弦AB最短时，∠ACB最小，此时圆心C与定点(1，2)的连线和直线2x－y＝0垂直，所以×2＝－1，解得a＝3.3．(2019届安徽合肥调研)已知直线l：x＋y－5＝0与圆C：(x－2)2＋(y－1)2＝r2(r>0)相交所得的弦长为2，则圆C的半径r＝(　　)A． B．2C．2 D．4解析：选B　解法一：由题意知圆C的圆心为(2，1)，圆心到直线l的距离d＝＝，又弦长为2，所以2＝2，所以r＝2，故选B．解法二：联立得整理得2x2－12x＋20－r2＝0，设直线与圆的两交点分别为A(x1，y1)，B(x2，y2)，则x1＋x2＝6，x1x2＝，所以|AB|＝|x1－x2|＝×＝×＝2，解得r＝2.【例】　(2019届河南信阳二模)若直线y＝kx＋1(k≠0)与圆x2＋(y－1)2＝1相交于A，B两点，C点坐标为(3，0)，若点M(a，b)满足＋＋＝0，则a＋b等于(　　)A．1 B．C． D．[解析]　设A(x1，y1)，B(x2，y2)．圆x2＋(y－1)2＝1的圆心为N(0，1)，又知直线y＝kx＋1(k≠0)恒过定点(0，1)，即圆心N，所以x1＋x2＝0，y1＋y2＝2.因为＋＋＝0，所以点M为△ABC的重心，所以所以a＋b＝，故选C．[答案]　C►名师点津直线与圆的位置关系多与平面向量、不等式、概率等交汇应用考查，着重考查数学运算能力．|跟踪训练|直线x＋y＋t＝0与圆x2＋y2＝2相交于M，N两点，已知O是坐标原点，若|＋|≤||，则实数t的取值范围是________．解析：将|＋|≤||＝|－|两边平方，得·≤0，所以圆心到直线的距离d＝≤×＝1，解得－≤t≤，故实数t的取值范围是[－， ]．答案：[－， ]