辽宁省沈阳市法库县2021-2022学年八年级下学期期末数学试题(word版含答案)

这是一份辽宁省沈阳市法库县2021-2022学年八年级下学期期末数学试题(word版含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（下列各题备选答案中，只有一个答案是正确的，每小题2分，共20分）
1．下列图形中，是中心对称图形但不是轴对称图形的是（ ）
A． B． C． D．
2．下列等式中，从左到右的变形是因式分解的是（ ）
A． B． C． D．
3．以下列线段a，b，c的长为三边的三角形中，不能构成直角三角形的是（ ）
A． B． C． D．
4．在平面直角坐标系中，若将三角形上各点的横坐标都加上5，纵坐标保持不变，则所得图形在原图形的基础上（ ）
A．向左平移了S个单位长度 B．向下平移了5个单位长度
C．向右平移了5个单位长度 D．向上平移了5个单位长度
5．多边形的内角和不可能为（ ）
A． B． C． D．
6．已知中，，则的度数是（ ）
A． B． C． D．
7．已知不等式组其解集在数轴上表示正确的是（ ）
A． B．
C． D．
8．下列分式计算错误的是（ ）
A． B． C． D．
9．如图，在中，，BC的垂直平分线交AC于点D，交BC于点E，若，则AC的长为（ ）
A． B．9 C．12 D．6
10．如图，直线与直线相交于点，则关于x的不等式的解为（ ）
A． B． C． D．
二、填空题（每小题3分，共18分）
11．分解因式___________．
12．若分式有意义，则x满足的条件是___________．
13．如果一个等腰三角形有一个内角是，那么顶角度数为___________．
14．如图，的周长为36，对角线AC，BD相交于点O，点E是CD的中点，，则的周长为___________．
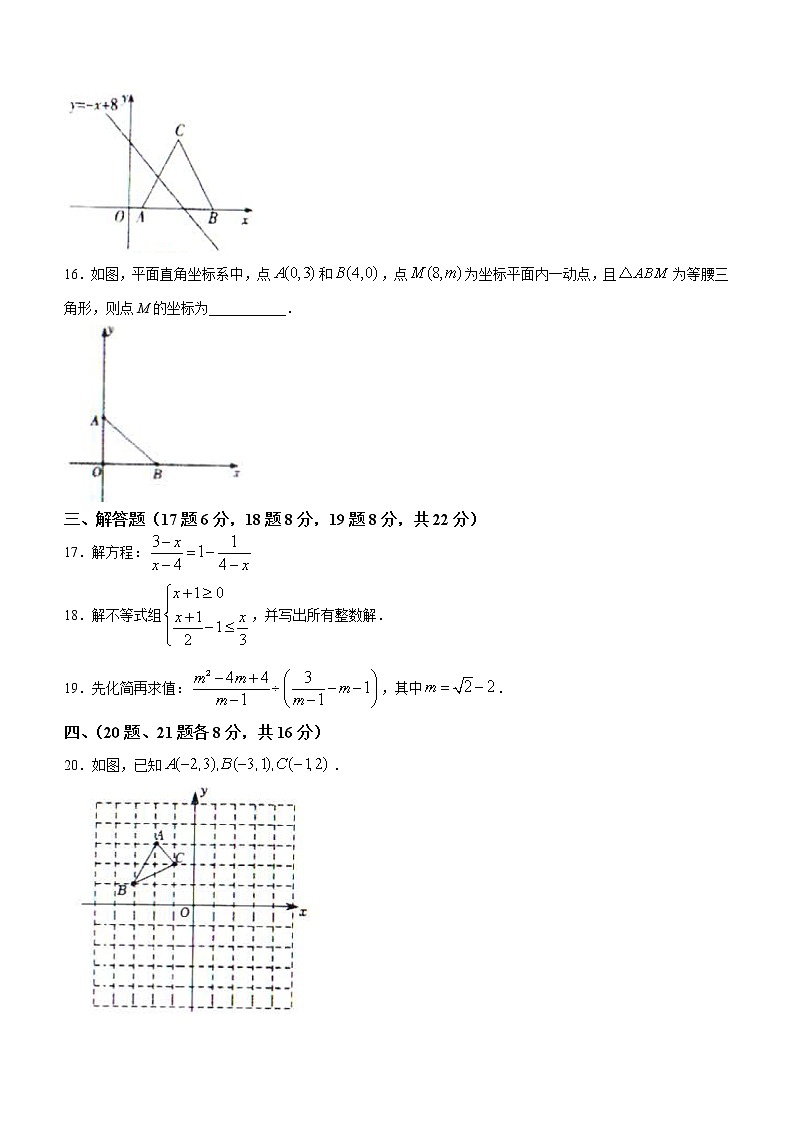
15．如图，中，，把放在平面直角坐标系中，且点A，B的坐标分别为，将沿x轴向左平移，当点C落在直线上时，平移的距离为___________．
16．如图，平面直角坐标系中，点和，点为坐标平面内一动点，且为等腰三角形，则点M的坐标为___________．
三、解答题（17题6分，18题8分，19题8分，共22分）
17．解方程：
18．解不等式组，并写出所有整数解．
19．先化简再求值：，其中．
四、（20题、21题各8分，共16分）
20．如图，已知．
（1）绕O逆时针旋转，得到，画出旋转后的；并直接写出点的坐标；
（2）作出关于原点O的中心对称图形．并直接写出点的坐标．
21．如图，在中，，过点A作于点E，连接BE，延长EA至点F，使，连接DF．求证：．
五、（本题10分）
22．如图，点C，B，D在同一直线上，和都是等边三角形．
（1）请找出图中的全等三角形，并说明理由；
（2）求证：．
六、（本题10分）
23．为加快产品生产的效率，某工厂将使用A，B两种型号机器生产产品，已知A型机器比B型机器每小时多生产，且A型机器生产所用时间与B型机器生产所用时间相等．
（1）求这两种机器每小时分别生产多少产品？
（2）该工厂为了在每小时以内至少完成产品生产的任务量，决定使用A，B两种型号机器共18台，并且同时开始生产产品，那么至少需要A型号机器多少台？
七、（本题12分）
24．如图，在中，于点D，BO平分，交CO于点O，，交AB于点E，连接CE．
（1）求证：；
（2）求证：CE平分；
（3）若，请直接写出CB的长度．
八、（本题12分）
25．如图，直线分别交x轴、y轴于A，B两点，直线BC与x轴交于点，P是线段AB上的一个动点（点P与A，B不重合）．
（1）求直线BC的函数表达式；
（2）设动点P的横坐标为t，的面积为S.
①求出S与t的函数关系式；
②在线段BC上存在点Q，使得四边形COPQ是平行四边形，请直接写出点Q的坐标．
法库县2021～2022学年度第二学期八年级期末考试
数学参考答案
注：多个解答题方法不唯一，请参考标准给分
一、选择题（每小题2分，共20分）．
1．A 2．B 3．D 4．C 5．D 6．C 7．D 8．C 9．B 10．A
二、填空题（每小题3分，共18分）．
11．； 12．； 13．50°或80°；
14．15； 15. 11； 16．（8，3）或
三、解答题：（17题6分，18题8分，19题8分，共22分）
17.解：
方程两边都乘得-----------2
解这个方程得 --------------------------4
经检验： 是原方程的根------------------6
18.解：解不等式，得，----------------2
解不等式，得≤ 3，--------------4
∴原不等式组的解集为-1≤≤ 3，-------------------6
∴整数解为-1，0，1，2，3.--------------------8
19.解：原式=---------------2
-------------------------4
，-------------------------------------------6
当时，
原式=
------------------------------------------7
．----------------------------------------8
四、（20题、21题每题8分，共16分）．
20．解：(1)如图，△A1B1C1即为所求，------------------2
点B1的坐标；------------------------4
(2)如图，△A2B2C2即为所求．--------------------6
B2（3，-1））---------------------------------8
21．证明：∵AE⊥CD，
∴∠FED=90°，----------------------------------1
∵四边形ABCD是平行四边形，∠ABC=45°，
∴AB//DC，AB=DC，∠ADE=∠ABC=45°---------------3
，--------------------------4
∴AE=DE，---------------------------------------5
∵CE=AF，
∴AB=EF，---------------------------------------6
在△FDE和△BEA中，
，
∴△FDE≌△BEA，-------------------------------7
∴DF=BE．--------------------------------------8
五、（本题10分）
22．解：（1）△ABE≌△ACD，---------------1
∵△ABC和△ADE都是等边三角形，
∴AE=AD，AB=AC,∠DAE=∠BAC-------------3
∴∠DAE+∠DAB=∠BAC+∠DAB
即∠BAE=∠CAD--------------------------4
∴△ABE≌△ACD；----------------------5
（2）证明：∵△ABE≌△ACD，
∴∠ABE=∠ACD，-----------------------7
∵△ABC是等边三角形，
∴∠ACD=∠BAC，----------------------8
∴∠ABE=∠BAC，---------------------9
∴BE//AC．--------------------------10
六、（本题10分）
23．解：(1)设A种型号机器每小时生产kg产品，B种型号机器每小时生产kg产品，根据题意得：，-------3
解得：，---------------------------4
经检验，是原方程的解，
则-10=50，-----------------------------5
答：A种型号机器每小时生产60kg产品，B种型号机器每小时生产50kg产品；---6
（2）设需要A型号机器台，则需要B型号机器台，
根据题意得：，----------------8
解得：，---------------------------------------9
答：至少需要A型号机器10台．-------------------------10
七、（本题12分）
24．解：（1）证明：∵∠ACB=90°，
∴∠ACD+∠BCD=90°，------------------1
∵CD⊥AB于点D，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠A=∠BCD；----------------------2
∵OE//AC，
∴∠A=∠OEB，------------------3
∴∠OEB=∠BCD=∠BCO，----------4
∵BO平分，
∴∠EBO=∠CBO，
在△BOE与△BOC中，
，
∴△BOE≌△BOC----------------------------6
（2）由（1）知△BOE≌△BOC
∴OC=OE----------------------------------7
∴∠OCE=∠OEC，---------------------------8
∵OE//AC，
∴∠ACE=∠OEC，---------------------------9
∴∠ACE=∠OCE，
即CE平分∠ACD；--------------------------10
（3）OB=--------------------------------12
八、（本题12分）
25.解：(1)直线分别交x轴、y轴于A,B两点，
∴点A的坐标为（4,0），---------------------------------1
点B的坐标为（0,4）．----------------------------------2
设直线BC的函数表达式为，
则，-------------------------------------3
解得--------------------------------------------------------4
故直线BC的函数表达式是．------------------5
(2)①∵点0(0,0)，点A(4,0)，
∴OA=4，----------------------------------------6
∵动点P的横坐标为t，P是线段AB上的一个动点(点P与A,B不重合)，
∴动点P的纵坐标为，-------------------------7
∴，
即S与t的函数关系式是．----------------9
②点Q的坐标为---------------------------------------12