2021-2022学年湖南省永州市宁远县八年级（下）期末数学试卷（Word解析版）

2021-2022学年湖南省永州市宁远县八年级（下）期末数学试卷

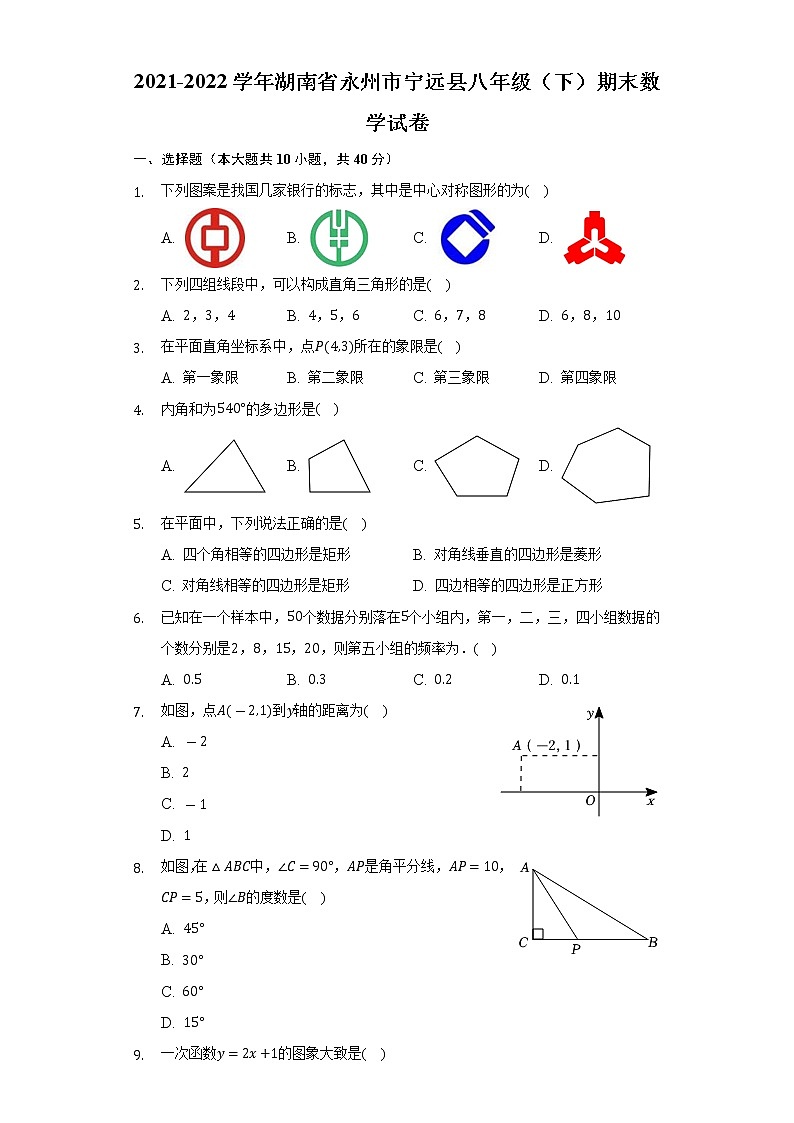
一、选择题（本大题共10小题，共40分）

1. 下列图案是我国几家银行的标志，其中是中心对称图形的为(    )

A.  B.  C.  D.

2. 下列四组线段中，可以构成直角三角形的是(    )

A. ，， B. ，， C. ，， D. ，，

3. 在平面直角坐标系中，点所在的象限是(    )

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

4. 内角和为的多边形是(    )

A.  B.  C.  D.

5. 在平面中，下列说法正确的是(    )

A. 四个角相等的四边形是矩形 B. 对角线垂直的四边形是菱形
C. 对角线相等的四边形是矩形 D. 四边相等的四边形是正方形

6. 已知在一个样本中，个数据分别落在个小组内，第一，二，三，四小组数据的个数分别是，，，，则第五小组的频率为．(    )

A.  B.  C.  D.

7. 如图，点到轴的距离为(    )

A.
B.
C.
D.

8. 如图，在中，，是角平分线，，，则的度数是(    )

A.
B.
C.
D.

9. 一次函数的图象大致是(    )

A.  B.
C.  D.

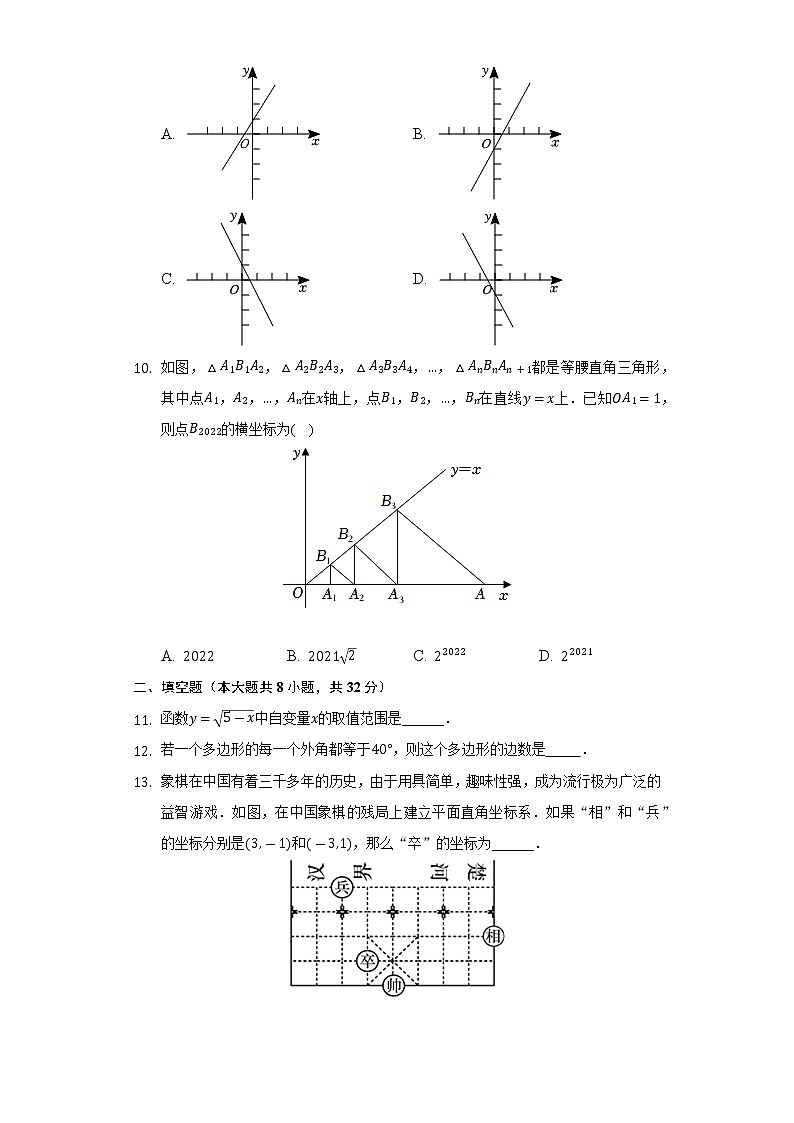
10. 如图，，，，，都是等腰直角三角形，其中点，，，在轴上，点，，，在直线上．已知，则点的横坐标为(    )

A.  B.  C.  D.

二、填空题（本大题共8小题，共32分）

11. 函数中自变量的取值范围是______．
12. 若一个多边形的每一个外角都等于，则这个多边形的边数是          ．
13. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图，在中国象棋的残局上建立平面直角坐标系．如果“相”和“兵”的坐标分别是和，那么“卒”的坐标为______．

14. 如图，、两点分别位于一个池塘的两端，小聪想用绳子测量、间的距离，但绳子不够长，一位同学帮他想了一个办法：先在地上取一个可以直接到达、的点，找到、的中点、，并且测出的长为，则、间的距离为______．

15. 如果正比例函数的图象经过点，那么的值等于______．
16. 学习委员调查本班学生课外阅读情况，对学生喜爱的书籍进行分类统计，其中“古诗词类”的频数为人，频率为，那么被调查的学生人数为______．
17. 在矩形中，对角线、相交于点，，，则的长是______．
18. 小高从家门口骑车去单位上班，先走平路到达点，再走上坡路到达点，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是______分钟．

三、解答题（本大题共8小题，共78分）

19. 如图，在中，，于，，求的长．

20. 已知：菱形的两条对角线与相交于点，且，，求菱形的周长和面积．

21. 已知点在函数的图象上，

求该函数的表达式；

求该函数图象与坐标轴围成的三角形的面积．

22. 如图，已知在平面直角坐标系中的位置如图所示，
    点关于轴对称点的坐标为______；
    将向下平移个单位得到，请画出；
    直接写出点的坐标是______．

23. 已知：如图，在四边形中，，，为对角线上两点，且，．
    求证：四边形为平行四边形．

24. 如图，，，是上的一点，且，．
    求证：≌．

25. 某社区为了进一步提高居民珍惜水、保护水和水忧患意识，提倡节约用水，从本社区随机抽取部分家庭，调查他们家庭每月的平均用水量，并将调查的结果制成如下不完整的统计图表：

请根据如图的统计图表，解答下列问题：
在频数分布表中，______，______；
根据题中数据补全频数分布直方图；
若该小区有户家庭，根据调查数据估计，该小区月均用水量超过的家庭大约有多少户？

26. 如图，在正方形中，点，分别是边，上的点，且连接，过点作，使，连接，．
    请判断：与的数量关系是______，位置关系是______；
    如图，若点，分别是边，延长线上的点，其它条件不变，中结论是否仍然成立？请作出判断并给予证明；
    如图，若点，分别是边，延长线上的点，其它条件不变，中结论是否仍然成立？请直接写出你的判断．
     

答案和解析

1.【答案】 

【解析】解：、是中心对称图形．故本选项正确；
B、不是中心对称图形．故本选项错误；
C、不是中心对称图形．故本选项错误；
D、不是中心对称图形．故本选项错误．
故选：．
根据轴对称图形与中心对称图形的概念求解．
本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转度后与原图重合．
 

2.【答案】 

【解析】解：、，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；
B、，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；
C、，不符合勾股定理的逆定理，不能构成直角三角形，故本选项不符合题意；
D、，符合勾股定理的逆定理，能构成直角三角形，故本选项符合题意．
故选：．
根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形，逐一判定即可．
本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．
 

3.【答案】 

【解析】解：点的横坐标和纵坐标均大于，
点所在的象限是第一象限．
故选：．
根据各象限内点的坐标特征解答即可．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．
 

4.【答案】 

【解析】解：设多边形的边数是，则
，
解得．
故选：．
根据多边形的内角和公式列式进行计算即可求解．
本题主要考查了多边形的内角和公式，熟记公式是解题的关键．
 

5.【答案】 

【解析】解：四个角相等的四边形是矩形，正确；
B.对角线垂直的平行四边形是菱形，故错误；
C.对角线相等的平行四边形是矩形，故错误；
D.四边相等的四边形应是菱形，故错误；
故选：．
根据矩形、菱形、正方形的判定定理，即可解答．
本题考查了矩形、菱形、正方形的判定，解决本题的关键是熟记矩形、菱形、正方形的判定定理．
 

6.【答案】 

【解析】解：根据题意，得
第五组的频数是，
则其频率是．
故选：．
根据总数以及四个小组的数据，得到第五组的频数，再根据频率频数总数进行计算，即可得出答案．
此题考查了频数与频率，掌握频率频数总数是解题的关键．
 

7.【答案】 

【解析】解：点的坐标为，则点到轴的距离为．
故选：．
根据点到轴的距离等于纵坐标的绝对值，到轴的距离等于横坐标的绝对值解答．
本题考查了点的坐标，熟记点到轴的距离等于纵坐标的长度，到轴的距离等于横坐标的长度是解题的关键．
 

8.【答案】 

【解析】解：在中，，，，
则．
故．
是角平分线，
．
．
故选：．
在直角中，由推知；然后根据角平分线的定义推知；最后由直角三角形的两个锐角互余求得的度数．
本题主要考查了角平分线的定义和含度角的直角三角形．在直角三角形中，度角所对的直角边等于斜边的一半．
 

9.【答案】 

【解析】解：在一次函数中，，，
一次函数图象经过第一、二、三象限，
故选：．
根据一次函数的系数即可确定图象．
本题考查了一次函数的图象，熟练掌握一次函数的图象与系数的关系是解题的关键．
 

10.【答案】 

【解析】解：因为，
，，，
由此得出，
所以，
所以点的横坐标为，
故选：．
根据规律得出，，，，所以可得，进而解答即可．
此题考查一次函数图象上点的坐标，关键是根据规律得出进行解答．
 

11.【答案】 

【解析】解：若使函数有意义，
，
即．
故答案为．
根据二次根式的性质列出不等式，求出不等式的取值范围即可．
本题主要考查了函数自变量取值范围的知识点，注意：二次根式中的被开方数必须是非负数，否则二次根式无意义．
 

12.【答案】 

【解析】

【分析】
本题考查了多边形的外角和根据外角和的大小与多边形的边数无关，由外角和求正多边形的边数，是常见的题目，需要熟练掌握．
根据任何多边形的外角和都是度，利用除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．
【解答】
解：，即这个多边形的边数是．  

13.【答案】 

【解析】解答】解：如图所示：
“卒”的坐标为，
故答案为：．
根据平面直角坐标系确定坐标原点和，轴的位置，进而解答即可．
此题考查坐标确定位置，解题的关键就是确定坐标原点和，轴的位置．
 

14.【答案】 

【解析】解：、是和的中点，
．
故答案是：．
、是和的中点，则是的中位线，则依据三角形的中位线定理即可求解．
本题考查了三角形的中位线定理，正确理解定理是关键．
 

15.【答案】 

【解析】解：正比例函数的图象经过点，
，
解得：．
故答案为：．
把点的坐标代入函数解析式，就可以求出的值．
本题主要考查一次函数图象上点的坐标特征，经过点，说明点的坐标满足函数解析式．
 

16.【答案】 

【解析】解：设被调查的学生人数为人，
则有，
解得，
经检验是方程的解．
故答案为；
设被调查的学生人数为人，则有，解方程即可．
本题考查频数与频率、记住两者的关系是解题的关键，属于基础题．
 

17.【答案】 

【解析】解：四边形是矩形，
，
，
是等边三角形，
，
故答案为：
根据矩形的对角线相等且互相平分可得，由，判断出是等边三角形，根据等边三角形的性质求出即可．
本题考查了矩形的性质，等边三角形的判定与性质，熟记性质并判断出是等边三角形是解题的关键．
 

18.【答案】 

【解析】

【分析】
本题主要考查函数的图象的知识点，通过考查一次函数的应用来考查从图象上获取信息的能力．依据图象分别求出平路、上坡路和下坡路的速度，然后根据路程，求出时间即可．
【解答】

解：先算出平路、上坡路和下坡路的速度分别为、和千米分，
所以他从单位到家门口需要的时间是分钟．
故答案为．

19.【答案】解：，，
，
在中，由勾股定理得，
，
在中，． 

【解析】首先利用勾股定理求出的长，再次利用勾股定理可得的长．
本题主要考查了勾股定理，等腰三角形的性质等知识，熟练掌握勾股定理是解题的关键．
 

20.【答案】解：由菱形对角线性质知，，，且，
，
周长；
菱形对角线相互垂直，
菱形面积是．
综上可得菱形的周长为、面积为． 

【解析】由菱形对角线的性质，相互垂直平分即可得出菱形的边长，菱形四边相等即可得出周长，由菱形面积公式即可求得面积．
本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算的长是解题的关键，难度一般．
 

21.【答案】解：因为点在函数的图象上，
所以   
解得    
函数解析式为 ．
在中，令，
即   
得     ，
令   ，得  ，
所以，函数图象与轴、轴分别交于点和
函数图象与坐标轴围成的三角形即，． 

【解析】将点代入，运用待定系数法求解即可．
求出与轴及轴的交点坐标，然后根据面积公式求解即可．
本题考查待定系数法求函数解析式及三角形的面积的知识，难度不大，关键是正确得出函数解析式及坐标与线段长度的转化．
 

22.【答案】   

【解析】解：点的坐标为，
关于轴对称的点的坐标为．
故答案为：．
如图，即为所求．

由图可知，点的坐标为．
故答案为：．
根据轴对称的性质可得出答案．
根据平移的性质作图即可．
由图即可得出答案．
本题考查作图平移变换、轴对称变换，熟练掌握平移和轴对称的性质是解答本题的关键．
 

23.【答案】证明：，
，
，
，
，
在和中，
≌，
，
，
四边形为平行四边形． 

【解析】首先证明≌可得，再由条件可利用一组对边平行且相等的四边形是平行四边形证明四边形为平行四边形．
此题主要考查了平行四边形的判定，关键是掌握一组对边平行且相等的四边形是平行四边形．
 

24.【答案】证明：，
．
，，
．
和是直角三角形，而．
≌． 

【解析】此题比较简单，根据已知条件，利用直角三角形的特殊判定方法可以证明题目结论．
本题考查了直角三角形全等的判定及性质；主要利用了直角三角形全等的判定方法，也利用了等腰三角形的性质：等角对等边，做题时要综合利用这些知识．
 

25.【答案】   

【解析】解：，
，
；
故答案为：；；
补全频数分布直方图如图：

户．
答：该小区月均用水量超过的家庭大约有户．
运用频率频数数据总数即可求出、的值；
运用中的数据即可画出统计图；
样本估计总体即可求解．
本题主要考查的是统计表和统计图的应用，掌握频数、总数、频率之间的关系是解题的关键．
 

26.【答案】  ，  ；
过点作的延长线于点，
，
，
，
，
在与中，
，
≌，
，，
，
，
，
四边形是矩形，
，

四边形是正方形，
，


  ，仍成立． 

【解析】

解：，；

另解：过点作于，
易证：≌
，
另解：也可证明≌，
，
，，
，
，
四边形是是平行四边形，从而得证．
成立．
四边形是正方形，
，，
在与中，
，
≌，
，，
，
，

，
，
，
四边形平行四边形，
，
【分析】
只要证明四边形是平行四边形即可得出，；
构造辅助线后证明≌，利用对应边相等求证四边形是矩形后，利用等量代换即可求出，；
证明≌后，即可证明四边形是平行四边形．
本题三角形与四边形综合问题，涉及全等三角形的判定与性质，平行四边形的判定与性质．解题的关键是利用全等三角形的对应边相等进行线段的等量代换，从而求证出平行四边形．