2021-2022学年安徽省滁州市定远县育才学校高二下学期5月月考数学试题Word版含答案

滁州市定远县育才学校2021-2022学年高二下学期5月月考

理科数学试题

第I卷（选择题）

一、选择题（本大题共12小题  每小题5分， 满分60分）

1．已知数列的前项积为，且，则（       ）

A．-1 B．1 C．2 D．-2

2．定义为个正数的“均倒数”．若已知数列的前项的“均倒数”为，又，则（       ）．

A． B． C． D．

3．在数列中，对任意N*，都有为常数，则称为“等差比数列”下面对“等差比数列”的判断正确的是（       ）

A．可能为

B．等差数列一定是等差比数列

C．等比数列一定是等差比数列

D．通项公式为的数列一定是等差比数列

4．实数满足，则的最小值为（       ）

A． B． C． D．

5．已知，设函数若关于的不等式在上恒成立，则的取值范围为

A． B． C． D．

6．设函数和的图像的一个公共点为，且在该点处有相同的切线，则方程一定存在负根的区间是（       ）．

A． B． C． D．

7．已知函数，则（　　）

A． B． C． D．

8．已知，曲线在不同的三点，，处的切线均平行于x轴，则m的取值范围是（       ）

A． B． C． D．

9．某莲藕种植塘每年的固定成本是1万元，每年最大规模的种植量是8万千克，每种植1千克莲藕，成本增加0.5元.种植万千克莲藕的销售额（单位：万元）是（是常数），若种植2万千克，利润是2.5万元，则要使利润最大，每年需种植莲藕（       ）

A．8万千克 B．6万千克 C．3万千克 D．5万千克

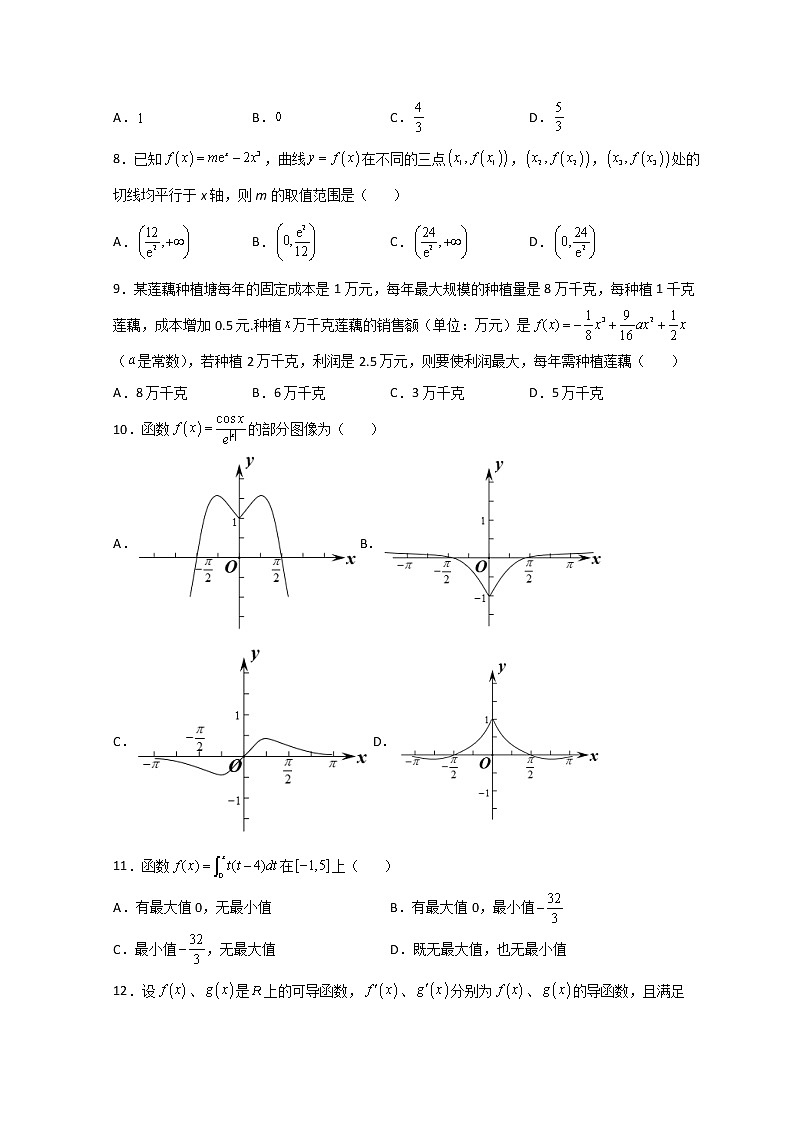
10．函数的部分图像为（       ）

A．B．

C．D．

11．函数在上（       ）

A．有最大值0，无最小值 B．有最大值0，最小值

C．最小值，无最大值 D．既无最大值，也无最小值

12．设、是上的可导函数，、分别为、的导函数，且满足，则当时，有（       ）

A． B．

C． D．

第II卷（非选择题）

二、填空题（本大题共4小题，共20分）

13．天干地支纪看法源于中国，中国自古便有十天干与十二地支.十天干：甲、乙、丙、丁、戊、已、庚、辛、壬、癸.十二地支：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配，排列起来，天干在前，地支在后，天干由“甲”起，地支由“子”起，比如第一年为“甲子”，第二年为“乙丑”，第三年为“丙寅”，…，以此类推，排列到“癸酉”后，天干回到“甲”重新开始，即“甲戌”，“乙亥”，之后地支回到“子”重新开始，即“丙子”，…，以此类推，已知2020年为庚子年，那么到建国100年时，即2049年以天干地支纪年法为__________.

14．设数列是等比数列，且，，则数列的前15项和为__________．

15．已知函数f(x)＝x4＋ax2－bx，且f′(0)＝－13，f′(－1)＝－27，则a＋b等于____．

16．直线分别与函数的图像相交于A､B两点，则的最小值为___________.

三、解答题（本大题共6小题，共70分）

17．（10分）已知函数，数列，，.

(1)求

(2)，求

18．（12分）在数列中，，．

(1)设，证明：是等比数列，并求的通项公式；

(2)设为数列的前项和，求．

19．（12分）已知曲线.

（1）当a=1时，求曲线在x=1处的切线方程；

（2）对任意的x∈[1，+∞)，都有，求实数a的取值范围.

20．（12分）已知函数，（）

（1）若，求曲线在处的切线方程.

（2）对任意，总存在，使得（其中为的导数）成立，求实数的取值范围.

21．（12分）设函数，曲线y=f（x）在点（2，f（2））处的切线方程为7x-4y-12=0．

（1）求y=f（x）的解析式；

（2）证明：曲线y=f（x）上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值，并求此定值．

22．（12分）已知函数（a为实数）．

(1)当时，求函数的单调区间；

(2)若函数在（0，1）内存在唯一极值点，求实数a的取值范围．

参考答案

1．A  2．D  3．D  4．D  5．C  6．A  7．A  8．D  9．B  10．D  11．B  12．A

13．巳

14．

15．18

16．3

17．(1)；

(2).

【解析】

 (1)由已知得，，整理得，且，

∴数列是首项为1，公差为3的等差数列，

∴，

故.

(2)∵，

∴

.

18．(1)解：因为，，

所以．

又，所以是首项为，公比为的等比数列．

所以，

故．

(2)，①

由①，得，②

①－②得，

，

所以．

19．（1）y=2x-1；（2）a≤2.

【解析】（1）函数f(x)的定义域为{x|x>0}，

当a=1时，，，，

所求切线方程为y-1=2(x-1)，即y=2x-1.

（2）由题意对于有则可得，x∈[1，+∞).

设，x∈[1，+∞)，，x∈[1，+∞)

再设m(x)=x2-lnx，x∈[1，+∞)，，m(x)在[1，十∞)上为增函数，

m(x)≥m（1）=1，即g'(x)>0，g(x)在[1，+∞)上为增函数，g(x)≥g（1）=2，即a≤2.

20．（1）；（2）.

【解析】（1）若，则若，

所以曲线在处的切线方程为

（2）对任意总存在，使得成立

得

①当时在单调递增所以在上的最小值为0.

在上的最小值为0，成立

②当时在上单调递减，在单调递增，所以在上的最小值为，在上的最小值为

由得得

③当时在单调递减所以在上的最小值为

在上的最小值为

由得无解

综上实数的取值范围为

21． 解：(1)方程7x－4y－12＝0可化为y＝x－3，

当x＝2时，y＝．

又f′(x)＝a＋，

于是，解得

故f(x)＝x－．

(2)证明：设P(x0，y0)为曲线上任一点，由f′(x)＝1＋知，曲线在点P(x0，y0)处的切线方程为y－y0＝(1＋)·(x－x0)，即y－(x0－)＝(1＋)(x－x0)．

令x＝0得，y＝－，从而得切线与直线x＝0，交点坐标为(0，－)．

令y＝x，得y＝x＝2x0，从而得切线与直线y＝x的交点坐标为(2x0,2x0)．

所以点P(x0，y0)处的切线与直线x＝0，y＝x所围成的三角形面积为|－||2x0|＝6．

曲线y＝f(x)上任一点处的切线与直线x＝0和直线y＝x所围成的三角形面积为定值，此定值为6．

22．(1)单调递减区间为（0，1），递增区间为

(2)

(1)解：函数的定义域为，．

当时，，

所以当时，；当时，．

所以的单调递减区间为（0，1），递增区间为．

(2)

由（1）知，当时，在（0，1）内单调递减，

所以在（0，1）内不存在极值点；

当时，要使函数在（0，1）内存在唯一极值点，

则在（0，1）内存在唯一变号零点，

即方程在（0，1）内存在唯一根，

所以在（0，1）内存在唯一根，

即与的图象在（0，1）内存在唯一交点，

因为，

所以在（0，1）内单调递减．又，

当时，，

所以，即a的取值范围为．