2021-2022学年广西钦州市第一中学高二下学期期中考试数学（文）试题含解析

这是一份2021-2022学年广西钦州市第一中学高二下学期期中考试数学（文）试题含解析，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
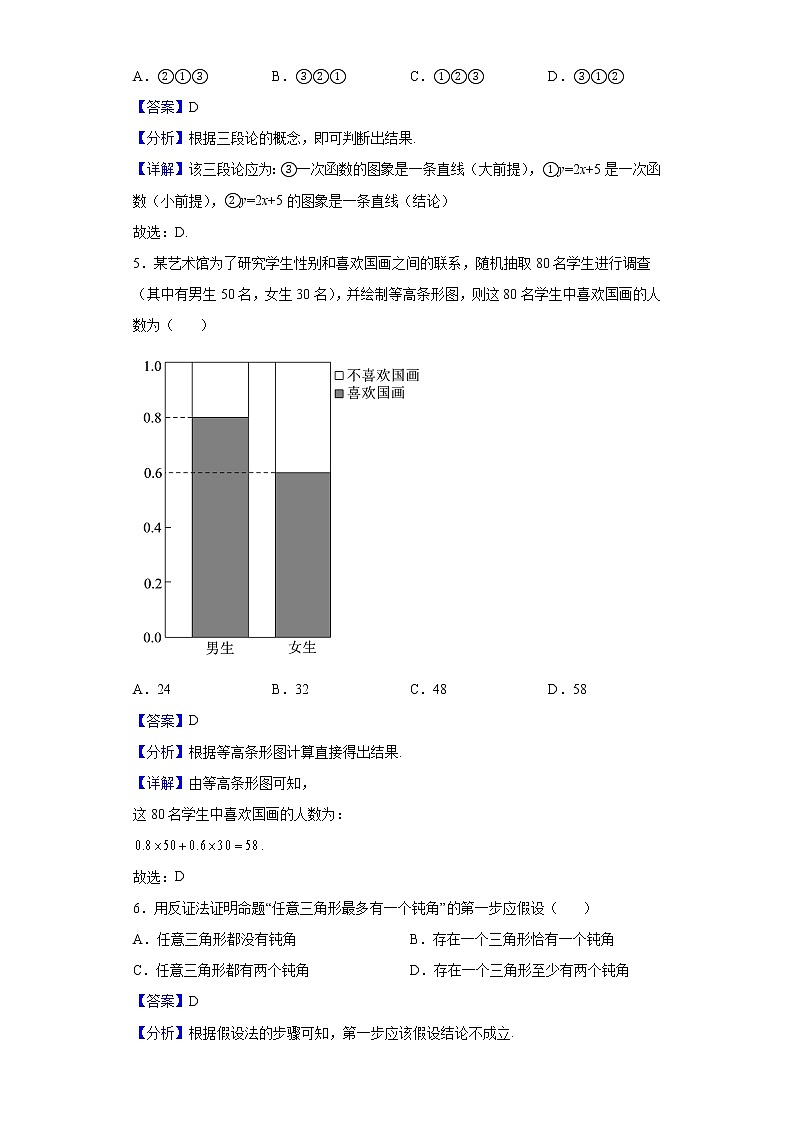
2021-2022学年广西钦州市第一中学高二下学期期中考试数学（文）试题一、单选题1．命题“，”的否定是（       ）A．， B．，C．， D．，【答案】D【分析】由全称命题的否定可直接得到结果.【详解】由全称命题的否定知原命题的否定为：，.故选：D.2．设，则“”是“”的(       )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】B【分析】根据二次不等式解法解不等式，根据充分条件和必要条件的概念即可判断.【详解】，设A＝{x|}，B＝{x|}，∵BA，∴“”是“”的充分不必要条件，“”是“”的必要不充分条件.故选：B.3．复数（为虚数单位）的虚部为（       ）A． B． C． D．【答案】D【分析】根据复数的定义判断.【详解】由复数的定义可得，复数的虚部为.故选：D4．由①是一次函数；②的图象是一条直线；③一次函数的图象是一条直线.写一个“三段论”形式的正确推理，则作为大前提､小前提和结论的分别是（       ）A．②①③ B．③②① C．①②③ D．③①②【答案】D【分析】根据三段论的概念，即可判断出结果.【详解】该三段论应为：③一次函数的图象是一条直线（大前提），①y=2x+5是一次函数（小前提），②y=2x+5的图象是一条直线（结论）故选：D.5．某艺术馆为了研究学生性别和喜欢国画之间的联系，随机抽取80名学生进行调查（其中有男生50名，女生30名），并绘制等高条形图，则这80名学生中喜欢国画的人数为（       ）A．24 B．32 C．48 D．58【答案】D【分析】根据等高条形图计算直接得出结果.【详解】由等高条形图可知，这80名学生中喜欢国画的人数为：.故选：D6．用反证法证明命题“任意三角形最多有一个钝角”的第一步应假设（       ）A．任意三角形都没有钝角 B．存在一个三角形恰有一个钝角C．任意三角形都有两个钝角 D．存在一个三角形至少有两个钝角【答案】D【分析】根据假设法的步骤可知，第一步应该假设结论不成立.【详解】第一步应该假设结论不成立，则应该假设“存在一个三角形有两个或三个钝角”或“存在一个三角形至少有两个钝角”.故选：D.7．观察下列算式:21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…，用你所发现的规律可得22019的末位数字是（       ）A．2 B．4 C．6 D．8【答案】D【分析】观察2的次方的末位数字，发现规律，即可计算的末位数字.【详解】由题意得，2的次方的末位数字分别是2，4，8，6这4个数字循环，即以4为周期．又，∴的末位数字与 的末位数字相同，∴的末位数字是8．故选：D．8．如图，图形中的圆是正方形ABCD的内切圆．点E，F，G，H为对角线AC，BD与圆的交点，若向正方形内随机投入一点，则该点落在阴影部分区域内的概率为（       ）A． B．C． D．【答案】D【分析】利用几何概型中的面积型，求阴影面积与正方形的面积比，即可得概率.【详解】设正方形的边长为2，则正方形面积为4，阴影部分的面积为，故若向正方形内随机投入一点，则该点落在阴影部分区域内的概率为．故选：D9．2020年春季，新冠肺炎疫情在全球范围内相继爆发，因为政治制度、文化背景等因素的不同，各个国家疫情防控的效果具有明显差异、如图是西方某国在60天内感染新冠肺炎的累计病例人数y（万人）与时间t（天）的散点图，则下列最适宜作为此模型的回归方程的类型是（     ）A． B．C． D．【答案】C【分析】根据散点图，根据常见函数的图象即得.【详解】根据散点图，可以看出，散点大致分布在一条“指数型”函数曲线附近，选项A对应的“直线型”的拟合函数；选项B对应的“幂函数型”的拟合函数；选项D对应的“对数型”的拟合函数；故选：C.10．有3个兴趣小组，甲、乙两人各自只参加其中一个，每位同学参加各小组的可能性相同，则这两位同学不在同一兴趣小组的概率为（       ）A． B． C． D．【答案】B【分析】利用列举法，结合古典概型的概率计算公式计算出所求概率.【详解】设小组的编号为，甲、乙两人各自只参加其中一个，可能为，共种，其中两位同学不在同一兴趣小组的为，共种，所以两位同学不在同一兴趣小组的概率为.故选：B11．已知平面内两定点，，下列条件中满足动点的轨迹为双曲线的是（       ）A． B．C． D．【答案】C【分析】由双曲线的定义即可求解.【详解】解：由题意，因为，所以由双曲线的定义知，当时，动点的轨迹为双曲线，故选：C.12．如图是函数的导数的图象，则下面判断正确的是（       ）A．在内是增函数B．在内是增函数C．在时取得极大值D．在时取得极小值【答案】B【分析】根据图象判断的单调性，由此求得的极值点，进而确定正确选项.【详解】由图可知，在区间上,单调递减；在区间上,单调递增.所以不是的极值点，是的极大值点.所以ACD选项错误，B选项正确.故选：B二、填空题13．设复数满足（为虚数单位），则______．【答案】【分析】利用复数的除法化简复数，利用复数的模长公式可求得结果.【详解】由已知可得，因此，.故答案为：.14．某中学高中部有三个年级，其中高三有人，采用分层抽样抽取一个容量为的样本.已知高一年级抽取人，高二年级抽取人，则高中部的总人数是____.【答案】【分析】先求出样本中高三学生人数，再根据分层抽样求总人数即可.【详解】因为抽取样本容量为，且高一年级抽取人，高二年级抽取人，那么高三年级抽取人，设高中部学生数为，则，得人.故答案为：.15．若椭圆的焦点在y轴上，则实数k的取值范围是___________.【答案】【分析】由椭圆的标准方程的特征列方程组求解可得.【详解】因为椭圆的焦点在y轴上，所以，解得，即实数k的取值范围为.故答案为：16．已知抛物线的焦点为，点在抛物线上，点在抛物线的准线上，若，且，则到的距离为______.【答案】12【分析】过点作于点，根据题意和抛物线的定义可得，进而得到关于p的方程，解方程即可.【详解】由知，为线段上靠近的三等分点，过点作于点，∴，∵，∴，解得.故答案为：12三、解答题17．已知函数．（1）求的解集；（2）若，求的最小值．【答案】（1）或；（2）.【分析】（1）由题意可得，然后去绝对值解出不等式即可；（2）利用绝对值不等式的几何意义直接得结果．【详解】（1）因为，， 所以，即或，所以或， 所以不等式的解集为或．（2）因为，所以；因为，所以的最小值为.【点睛】本题考查了绝对值不等式的解法和绝对值不等式的几何意义，正确的理解绝对值不等式的几何意义很关键，属基础题．18．在直角坐标系 中，直线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）写出直线的普通方程与曲线的直角坐标方程；（2）求直线被曲线截得的弦长.【答案】（1），；（2）.【解析】（1）利用消参法即可得直线的普通方程，根据极坐标与直角坐标的关系即可得曲线C的方程；（2）由（1）知曲线C为圆，根据圆的性质，结合点线距离公式，即可求弦长.【详解】（1）由直线的参数方程( t为参数可得其普通方程为：；由曲线的极坐标方程得，所以曲线的直角坐标方程为：.（2）由（1）得曲线：，圆心到直线的距离为：，所以直线被曲线截得的弦长为：.19．6月17日是联合国确定的“世界防治荒漠化和干旱日”，旨在进一步提高世界各国人民对防治荒漠化重要性的认识，唤起人们防治荒漠化的责任心和紧迫感.为增强全社会对防治荒漠化的认识与关注，聚集联合国2030可持续发展目标——实现全球土地退化零增长.自2004年以来，我国荒漠化和沙化状况呈现整体遏制、持续缩减、功能增强、成效明显的良好态势.治理沙漠离不开优质的树苗，现从苗圃中随机地抽测了400株树苗的高度（单位：），得到如图所示的频率分布直方图.(1)求频率分布直方图中实数的值和抽到的树苗的高度在的株数；(2)估计苗圃中树苗的高度的平均数和中位数.（同一组中数据用该组区间的中点值作代表）【答案】(1)，342(2)189.8，190【分析】（1）由每个小长方形的面积的总和等于，即可通过列方程求出值，根据频数样本容量频率即可求出抽到的树苗的高度在的株数；（2）由频率分布直方图中每个小长方形的面积与对应小正方形底边中点的横坐标的乘积之和即为平均数，即可算出，利用平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标即为中位数，即可算出.【详解】(1)∵，∴，抽到的树苗的高度在的株数为（株）(2)苗圃中树苗的高度的平均数：设中位数为，因为，，则，，所以.20．现在微信支付已成为人们日常流行的一种付款方式，因为它比现金支付更快捷、更方便. 某大型超市为了鼓励顾客使用微信付款，特举办微信支付活动一个月，规定：凡是在这个月内使用微信付款次数达到60次即有精美奖品，否则无奖品. 现从该超市数据信息中随机选取已使用微信付款的40名顾客，且男、女比例相同，将他们的数据整理如下表：       次数性别男23276女13862 (1)根据题意完成下面的列联表，并据此判断能否有的把握认为“是否获奖”与“性别”有关？ 有奖无奖总计男   女   总计    (2)在这40名顾客中，从支付次数达到70的人中随机抽取2人，求至少抽取1名女性的概率.   附：参考公式：参考数据：0.1000.0500.0100.0050.001k2.7063.8416.6357.87910.828 【答案】(1)列联表见解析，没有的把握认为“是否获奖”与“性别”有关.(2)【分析】（1）根据题意填写列联表，由表中数据计算观测值，对照临界值即可得出结论;（2）分别求出支付次数达到70的人中随机抽取2人的事件总数和抽取2人中至少含有1名女性的事件数，然后直接利用古典概型的公式求解即可.(1) 有奖无奖总计男13720女81220总计211940 ∴没有的把握认为“是否获奖”与“性别”有关.(2)支付次数达到70的顾客共8人，其中6名男性，记为，2名女性，记为，记事件为从8人中随机抽取2人，至少含有1名女性，所有可能结果列表如下： ABCDEFabA B  C   D    E     F      a       b         则基本事件总个数为，其中包含的基本事件个数为13，故.21．已知的一个极值点为2.（1）求函数的单调区间；（2）求函数在区间上的最值.【答案】（1）在区间上单调递减，在区间，上单调递增；（2）最小值为，最大值为13.【分析】（1）根据极值点先求出的值,再求出,令或,得到函数的单调区间；（2）求出函数在上的单调性，根据极值和端点值的比较可得到最值.【详解】（1）因为，所以，因为的一个极值点为2，所以，解得，此时，，令，得或，令，得；令，得或，故函数在区间上单调递减，在区间，上单调递增.（2）由（1）知，在上为增函数，在上为减函数，所以是函数的极大值点，又，，，所以函数在区间上的最小值为，最大值为.22．已知椭圆C：的短轴长为2，且点在C上．(1)求椭圆C的标准方程；(2)设、为椭圆的左、右焦点，过的直线l交椭圆C与A、B两点，若的面积是，求直线l的方程．【答案】(1)；(2)或.【分析】(1)根据短轴长求出b，根据M在C上求出a；(2)根据题意设直线l为，与椭圆方程联立得根与系数关系，根据＝即可求出m的值.【详解】(1)∵短轴长为2，∴，∴，又∵点在C上，∴，∴，∴椭圆C的标准方程为；(2)由(1)知，∵当直线l斜率为0时，不符合题意，∴设直线l的方程为：，联立，消x得：，∵，∴设，，则，∵，∴，∴，即，解得，∴直线l的方程为：或.