初中数学北师大版九年级下册2 圆的对称性课文配套ppt课件

这是一份初中数学北师大版九年级下册2 圆的对称性课文配套ppt课件，共27页。PPT课件主要包含了一圆的对称性，在同圆或等圆中等内容，欢迎下载使用。

1.什么是轴对称图形?如果一个图形沿某条直线对折后，直线两旁的部分能够完全重合，那么这个图形叫作轴对称图形.这条直线叫这个图形的对称轴.
2.什么是中心对称图形？　　把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
1.掌握圆的轴对称性和中心对称性2.掌握圆心角的概念. 3.掌握在同圆或等圆中，圆心角、弦、弧中有一个量相等就可以推出其他的两个量对应相等，以及它们在解题中的应用.
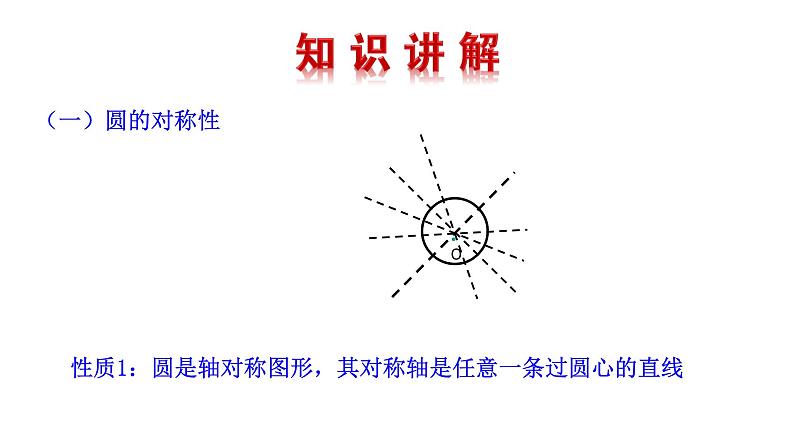
性质1：圆是轴对称图形，其对称轴是任意一条过圆心的直线
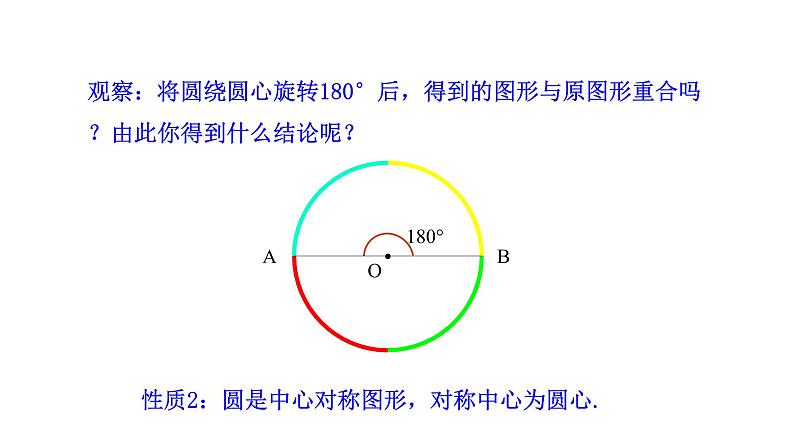
观察：将圆绕圆心旋转180°后，得到的图形与原图形重合吗？由此你得到什么结论呢？
性质2：圆是中心对称图形，对称中心为圆心.
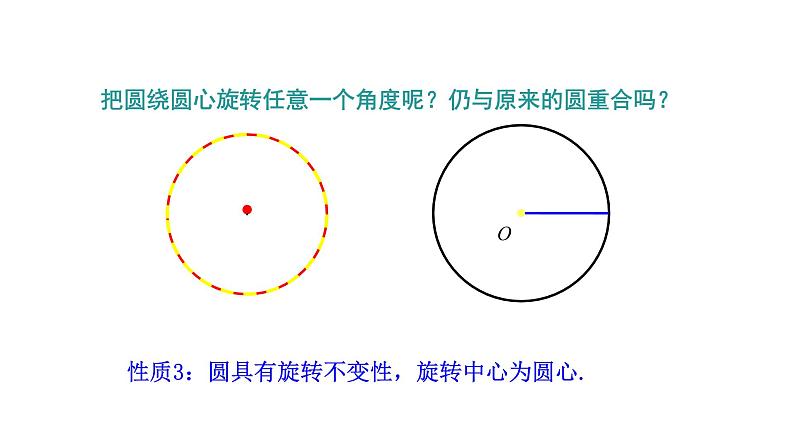
把圆绕圆心旋转任意一个角度呢？仍与原来的圆重合吗？
性质3：圆具有旋转不变性，旋转中心为圆心.
观察在⊙O中，这些角有什么共同特点？
1.顶点在圆心的角，叫圆心角，如∠AOB .
3.圆心角 ∠AOB所对的弦为AB.
任意给圆心角，对应出现三个量：
一条弧所对的圆心角只有一个 .
判一判：判别下列各图中的角是不是圆心角，并说明理由.
由圆的旋转不变性，我们发现： 在⊙O中，如果∠AOB = ∠COD，那么 ，弦AB = 弦CD
如图，在等圆中，如果∠AOB ＝∠CO ′ D，你发现的等量关系是否依然成立？为什么？
通过平移和旋转将两个等圆变成同一个圆，我们发现：如果∠AOB=∠CO ′D，那么，AB = CD，弦 AB = 弦 CD.
弧、弦与圆心角的关系定理
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
想一想：定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．”中，可否把条件“在同圆或等圆中”去掉？为什么？
弧、弦与圆心角关系定理的推论
在同圆或等圆中，相等的弦所对的圆心角相等，所对的弧也相等．
①∠AOB =∠COD
在同圆或等圆中,如果①两个圆心角；②两条弧；③两条弦,有一组量相等,那么它们所对应的其余各组量都分别相等.
对称轴有无数条，即过圆心的直线
弦、弧、圆心角的关系定理
1.如图，已知⊙O, ⊙E半径相等，AB、CD分别是⊙O、⊙E的两条弦.填空：
（1）若AB=CD，则 = ; 则 = .
（2）若AB= CD，则 = ; = .
（3）若∠ AOB= ∠ CED，则 = ，则 = .
2.已知：如图，AB,CD是⊙O的两条弦，OE,OF为AB,CD的弦心距，根据本节定理及推论填空： （1）如果AB=CD，那么 ___________,________, _________. （2）如果OE=OF，那么 ___________,________,__________.
2.已知：如图，AB,CD是⊙O的两条弦，OE,OF为AB,CD的弦心距，根据本节定理及推论填空： （3）如果 那么 ____________,__________,_________. （4）如果∠AOB=∠COD，那么 _________,________,_________.
3.如图，在⊙O中， ,∠ACB=60°，求证：∠AOB=∠BOC=∠AOC.
∴△ABC是等边三角形， AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
△ABC是等腰三角形.
证明：连接OA，OB，设分别与CD，EF交于点H，G∵A为 中点，B为 中点∴OA⊥CD，OB⊥EF.