初中数学北师大版九年级下册5 二次函数与一元二次方程背景图课件ppt

这是一份初中数学北师大版九年级下册5 二次函数与一元二次方程背景图课件ppt，共56页。PPT课件主要包含了b2-4ac＞0，a＞0，a＜0，b2-4ac0，x1x2，b2-4ac＜0，活动探究2，x1x22，想一想，解法1等内容，欢迎下载使用。
1、一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=______。当△﹥0时，方程根的情况是________________；当△=0时，方程根的情况是________________； 当△﹤0时，方程根的情况是______________。
2、二次函数y=ax2+bx+c(a、b、c是常数，且a≠0)图像是一条_____，它与x轴的交点有几种可能的情况？
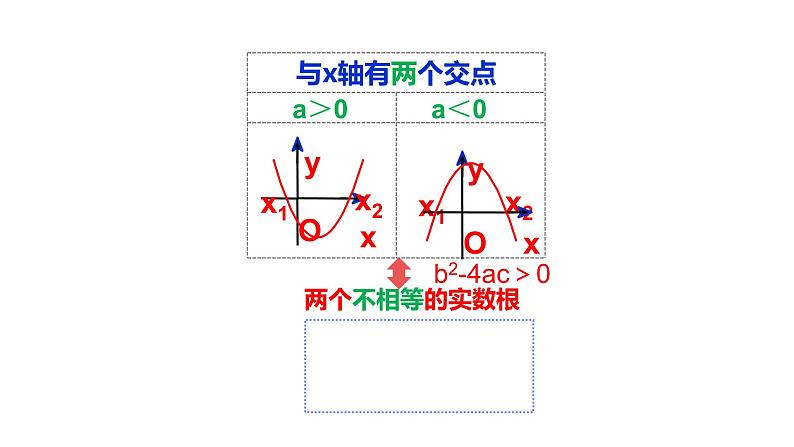
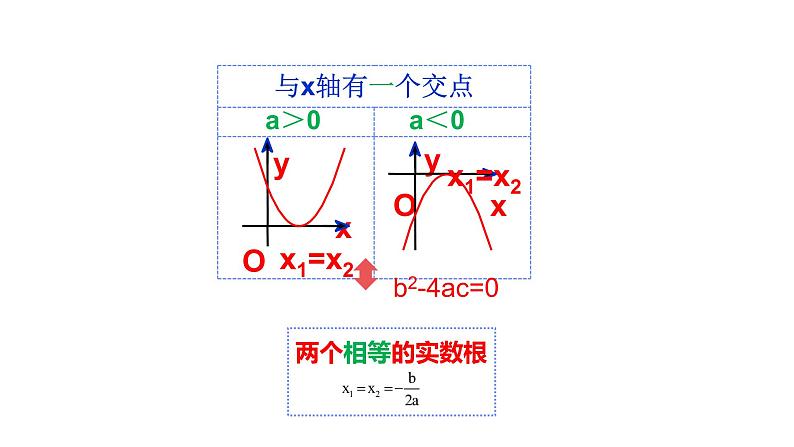
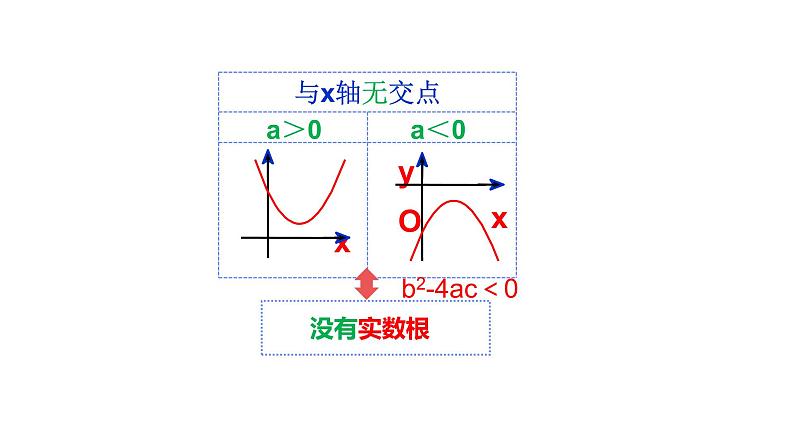
三种可能：①两个交点 ②一个交点 ③没有交点。
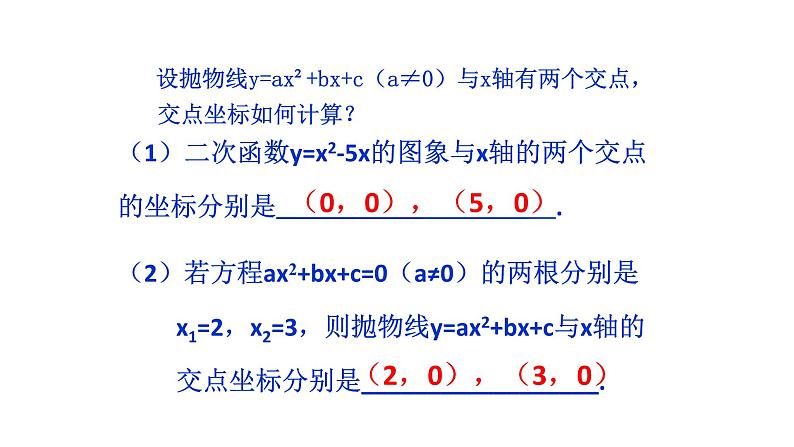
设抛物线y=ax²+bx+c（a≠0）与x轴有两个交点，交点坐标如何计算？
（1）二次函数y=x2-5x的图象与x轴的两个交点的坐标分别是　 　　 　.
（0，0），（5，0）
（2）若方程ax2+bx+c=0（a≠0）的两根分别是x1=2，x2=3，则抛物线y=ax2+bx+c与x轴的交点坐标分别是__________________.
（2，0），（3，0）
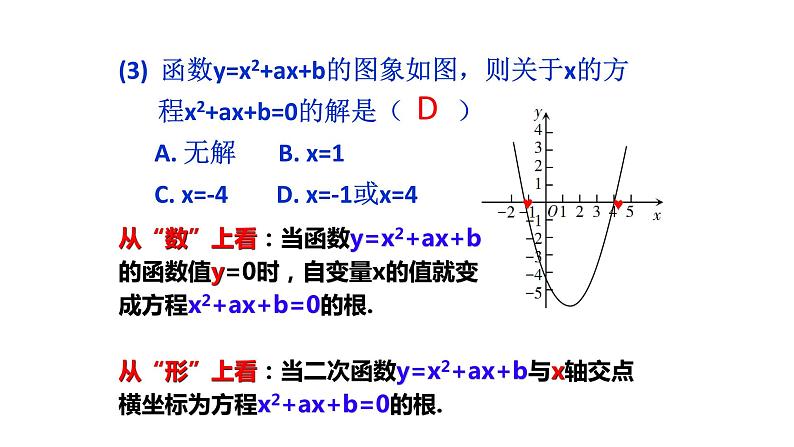
(3) 函数y=x2+ax+b的图象如图，则关于x的方程x2+ax+b=0的解是（　　） A. 无解 B. x=1 C. x=-4 D. x=-1或x=4
从“数”上看：当函数y=x2+ax+b的函数值y=0时，自变量x的值就变成方程x2+ax+b=0的根.
从“形”上看：当二次函数y=x2+ax+b与x轴交点横坐标为方程x2+ax+b=0的根.
1.经历探索二次函数与一元二次方程的关系的过程，体会方程与函数之间的联系.2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，理解何时方程有两个不等的实数根、两个相等的实数根和没有实数根.3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.
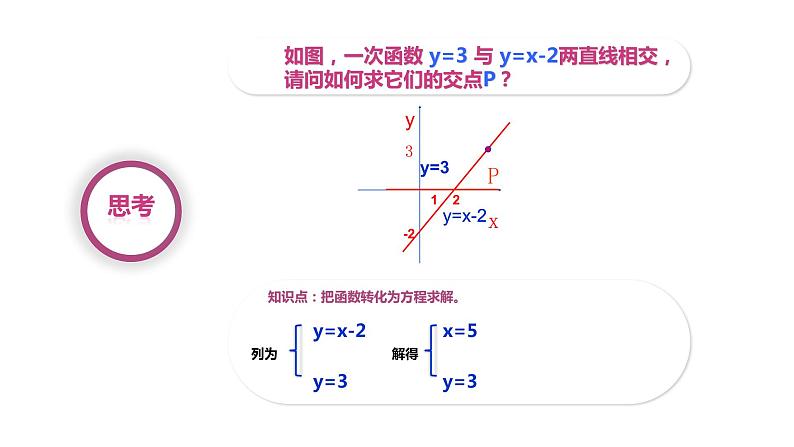
我们学习了一元一次方程kx＋b＝0(k≠0)和一次函数y＝kx＋b(k≠0)后，讨论了它们之间的关系．当一次函数中的函数值y＝0时，一次函数y＝kx＋b就转化成了一元一次方程kx＋b＝0，且一次函数y＝kx＋b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx＋b＝0的解．现在我们学习了一元二次方程ax2＋bx＋c＝0(a≠0)和二次函数y＝ax2＋bx＋c(a≠0)，它们之间是否也存在一定的关系呢？本节课我们将探索有关问题．
1.一元二次方程ax2+bx+c=0 的求根公式是什么？
当b2－4ac≥0时，
当b2－4ac0,c